極坐標 (Polar Coordinate)

Posted on 2013/10/22 in 數學 with 尚無留言 7,418 views

極坐標 (Polar Coordinate)
國立蘭陽女中數學科陳敏晧老師

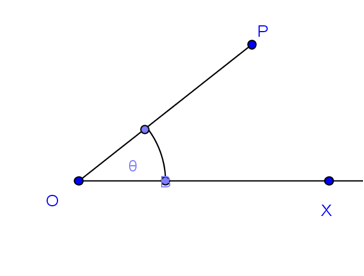
在數學領域中，坐標表示法除了直角坐標(Cartesian Coordinate)外，還有極坐標系統，這種系統是將一個點 \(P\) 與中心點 \(O\) (極點pole)連線成 \(\vec{OP}\)，過 \(O\) 點作一向右水平線(極軸pole axis)，以 \(\vec{OX}\) 為始邊，\(\vec{OP}\) 為終邊之有向角 \(\theta\)，

如圖一所示，令 \(r=\overline{OP}\)，若我們用 \((r,\theta)\) 來代表 \(P\) 的位置時，則稱 \((r,\theta)\) 為 \(P\) 之極坐標，其中稱 \(r\) 為「模」(modulus)，而 \(\theta\) 稱為「幅角」(argument)，當 \(0\le \theta<2\pi\) 時，稱為「主幅角」(principal argument)，另外，有向角的定義方式也與廣義角相同，即逆時針旋轉時為正角，順時針旋轉時為負角。

圖一

若將極點置於直角坐標系的原點，視極軸為 \(x\) 軸，

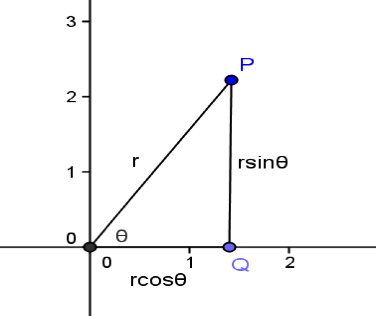
則極坐標 \((r,\theta)\) 的直角坐標為 \((r\cos\theta,r\sin\theta)\)；

若直角坐標 \((x,y)\) 的極坐標為 \((\sqrt{x^2+y^2},\theta+2k\pi),k\in\mathbb{Z}\)

或 \((-\sqrt{x^2+y^2},\theta+2k\pi+\pi),k\in\mathbb{Z}\)，

此時，\(\displaystyle\sin\theta= \frac{y}{{\sqrt {{x^2} + {y^2}} }},\cos \theta= \frac{x}{{\sqrt {{x^2} + {y^2}} }}\)，如圖二所示。

圖二

例如：
極坐標 \(\displaystyle\left( {4,\frac{\pi }{3}} \right)\) 的直角坐標為 \(\displaystyle\left( {4\cos \frac{\pi }{3},4\sin \frac{\pi }{3}} \right) = \left( {4 \times \frac{1}{2},4 \times \frac{{\sqrt 3 }}{2}} \right) = \left( {2,2\sqrt 3 } \right)\)；
而直角坐標 \(\left( {1,\sqrt 3 } \right)\) 的極坐標為
\(\displaystyle\left( {\sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} ,{{\tan }^{ – 1}}\left( {\frac{{\sqrt 3 }}{1}} \right)} \right) = \left( {2,\frac{\pi }{3}} \right)\)，
直角坐標 \((2,-3)\) 的極坐標為 \(\displaystyle\left( {\sqrt {{{\left( 2\right)}^2} + {{\left({-3}\right)}^2}} ,{\tan^{-1}}\left( {\frac{{-3}}{2}}\right)}\right)=\left({\sqrt {13} ,{{\tan}^{-1}}\left( {-\frac{3}{2}} \right)}\right)\)。

除了坐標轉換外，我們也可以將直角坐標系中的方程式用極坐標表示，例如：直線方程式 \(y=x\) 可用 \(\theta=45^\circ\) 表示；圓方程式 \(x^2+y^2=1\) 可用 \(r=1\) 表示，其他的圓錐曲線(拋物線、橢圓、雙曲線)轉換成極坐標方程式時就常會涉及到三角函數，例如：拋物線 \(y=\frac{x^2}{4}\) 會變成 \(r=\frac{1}{1-\sin\theta}\)。

對於很多類型的曲線，極坐標方程式最簡單的表達形式，如有內環的蚶線(limaçon)：\(r=1+2\cos\theta\)；四瓣玫瑰線(rose curve)：\(r=2\cos{2\theta}\)；對數螺線(logarithmic spiral)亦稱為等角螺線：\(r=ae^{b\theta}\) 或 \(\theta=\frac{1}{b}\ln(\frac{r}{a})\)；雙紐線(lemniscate)：\(r=4\sin{2\theta}\)；亨利的蝴蝶線(Henri’s Butterfly)：\(r=(\sin{4\theta})^2+\cos{3\theta}\)。

牛頓(Sir Isaac Newton, 1642-1727)在 1736 年出版的《流數法(Method of Fluxions)》一書中，將極坐標系應用於表示平面上的任何一點。牛頓在書中驗證了極坐標和其他九種坐標系的轉換關係。雅各布．伯努力(Jacob Bernoulli, 1654- 1705)在 1691 年出版的《博學通報(Acta eruditorum)》一書中正式使用定點和從定點引出的一條射線，他將定點稱為極點，射線稱為極軸，平面內任何一點的坐標都可以用通過該點與定點的距離和與極軸的夾角來表示。

總之，除了數學外，極坐標系的應用層面也十分廣泛，包括物理、工程、航海以及機器人領域。

參考資料：