最短路徑問題

最短路徑問題
臺北市立西松高中 蘇惠玉教師

在數學III的直線單元中有這樣的問題：在坐標平面上，給定兩點 \(A\) 與 \(B\)，以及一直線 \(L\)，想要在 \(L\) 上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值。這個 \(P\) 點要怎麼找呢？我們先把 \(L\) 特殊化，從 \(x\) 軸上的點來考慮。

例題1
坐標平面上給定兩點 \(A(1,3),B(5,-1)\)。
在 \(x\) 軸上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值，\(P\) 點坐標為何？

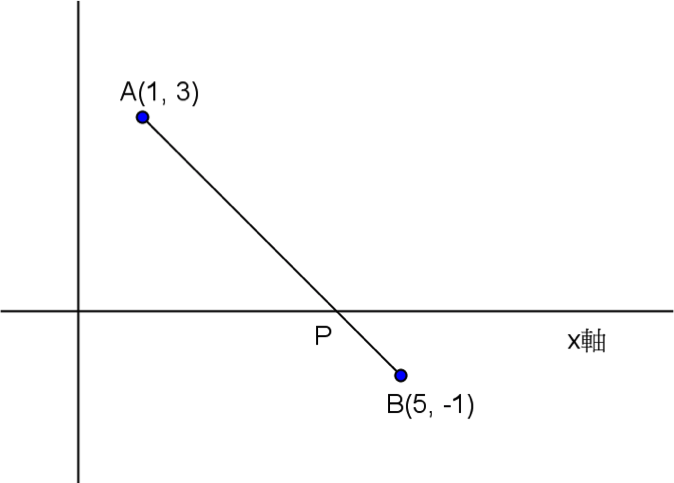
解：如圖，\(A,B\) 在 \(x\) 軸的異側。
由於兩點連線會與 \(x\) 軸相交，且兩點間直線距離最近，
因此當 \(P\) 點為 \(\overline{AB}\) 與 \(x\) 軸的交點時，此時 \(\overline{PA}+\overline{PB}\) 有最小值。
因為 \(\overleftrightarrow{AB}\) 的方程式為 \(x+y=4\)，故與 \(x\) 軸的交點為 \(P(4,0)\)，
此時所求最小值為 \(\overline{AB}=4\sqrt{2}\)。
由例題1可知，當 \(A,B\) 在所給直線 \(L\) 的異側時，
所要找的 \(P\) 點即為 \(\overleftrightarrow{AB}\) 與 \(L\) 的交點。
那麼當 \(A,B\) 都在 \(L\) 的同側時，要如何找到 \(P\) 點呢？

例題2
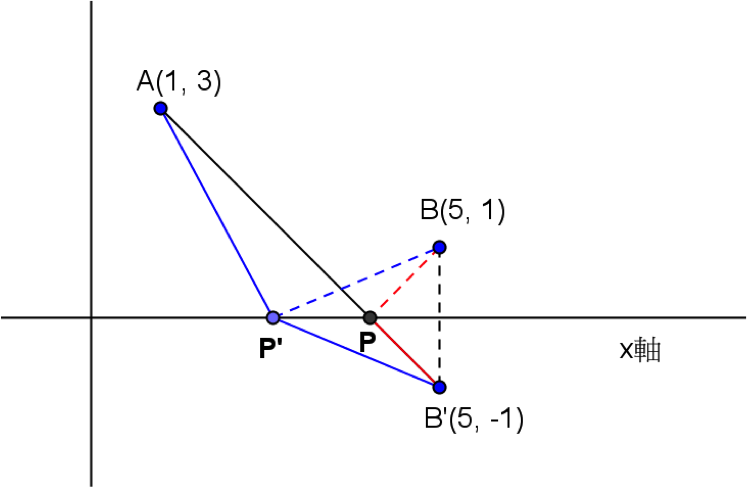
坐標平面上給定兩點 \(A(1,3),B(5,-1)\)。
在 \(x\) 軸上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值，\(P\) 點坐標為何？

解：如圖，\(A,B\) 在 \(x\) 軸的同側。
由例題1知道當兩點在異側時，只要考慮這兩點的連線與 \(x\) 軸的交點即可。
因此考慮作 \(B\) 點對 \(x\) 軸的對稱點 \(B'(5,1)\)，
此時 \(A\) 與 \(B’\) 在 \(x\) 軸的異側，連接 \(\overleftrightarrow{AB’}\)，與 \(x\) 軸交於 \(P\) 點。
此時因為 \(\overline{PB}=\overline{PB’}\)，因此 \(\overline{PA}+\overline{PB}=\overline{PA}+\overline{PB’}=\overline{AB’}\)。
而在 \(x\) 軸上的任一點 \(P’\)，因為 \(\overline{P’B}=\overline{P’B’}\)，
因此 \(\overline {P’A}+\overline {P’B} = \overline {P’A} + \overline {P’B’}\ge\overline {AB’}=\overline{PA} +\overline{PB}\)
亦即此時的 \(P\) 點為 \(x\) 軸上使得 \(\overline{PA}+\overline{PB}\) 有最小值的點。
因為 \(\overleftrightarrow{AB’}\) 的方程式為 \(x+y=4\)，故與 \(x\) 軸的交點為 \(P(4,0)\)，
此時所求最小值為 \(\overline{AB’}=4\sqrt{2}\)。

由例題2可知，當給定的兩點 \(A,B\) 在直線 \(L\) 的同側時，
只要先找 \(B\) 點對 \(L\) 的對稱點 \(B’\) (找 \(A\) 點對 \(L\) 的對稱點 \(A’\) 亦可)，連接 \(\overleftrightarrow{AB’}\)，
與直線 \(L\) 的交點 \(P\) 即為所求之點，此時 \(\overline{PA}+\overline{PB}\) 的最小值為 \(\overline{AB’}\)。

例題3
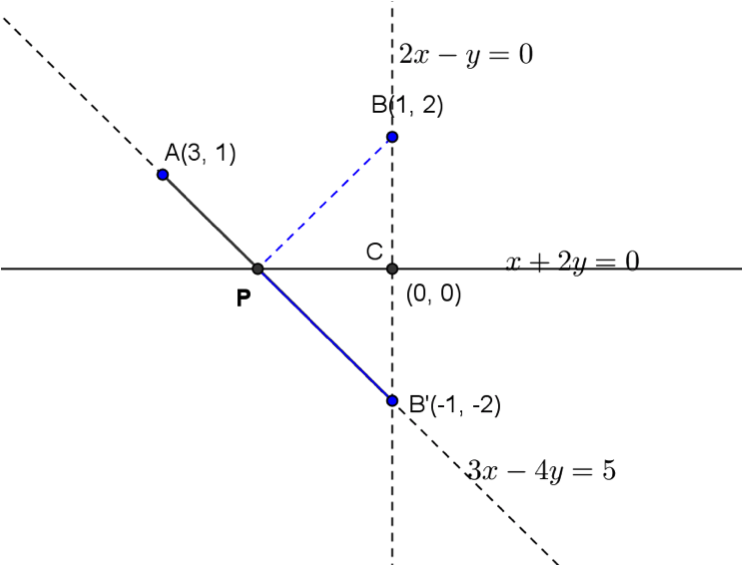
坐標平面上給定兩點 \(A(3,1),B(1,2)\)。
在直線 \(L:x+2y=0\) 上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值，\(P\) 點坐標為何？

解：

1. 先作點 \(B(1,2)\) 對 \(L\) 的對稱點 \(B’\)：過 \(B\) 與 \(L\) 垂直的直線為 \(2x-y=0\)，
   此直線與 \(L\) 的交點為 \((0,0)\)，此點為 \(B\) 與 \(B’\) 的中點，因此 \(B'(-1,-2)\)；
2. 連 \(\overleftrightarrow{AB’}\)，其方程式為 \(3x-4y=5\)；
3. 求 \(\overleftrightarrow{AB’}\) 與 \(L\)的交點：\(\left\{ \begin{array}{l} 3x – 4y = 5\\ x + 2y = 0 \end{array} \right.\)，\(x=1,y=-\frac{1}{2}\)
4. \(P(1,-\frac{1}{2})\) 即為所求，此時的最小值 \(=\overline{AB’}=5\)。

接下來我們換個角度從物理來看例題3的問題。
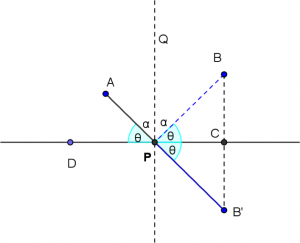
在例題3解法的圖中，
因為 \(B’\) 為 \(B\) 對 \(L\) 的對稱點，
因此 \(\angle BPC=\angle CPB’=\angle APD=\theta\)，
因此過 \(P\) 點作 \(L\) 的垂直線 \(\overleftrightarrow{QP}\)，
可得 \(\angle BPQ=\angle QPA=\alpha\)。
由此可知，若有一光經過 \(B\) 點射向 \(L\) 時，
會由 \(P\) 點反射經過 \(A\) 點。
但是由光學性質知道，
光在行進時會依最省時路徑前進，
亦即由 \(B\) 點射向 \(L\)，反射經過 \(A\) 點之光的行進路線，
會選擇直線 \(L\)上 使得 \(\overline{PA}+\overline{PB}\) 有最小值的 \(P\) 點作為反射點。
同時，由於 \(A,P,B’\) 三點共線，也可知反射線（\(\overleftrightarrow{AP}\)）會經過 \(B\) 點的對稱點 \(B’\)。

用這樣的角度看例題3，同樣的解法卻可以換個問題情境來問，如例題4。

例題4
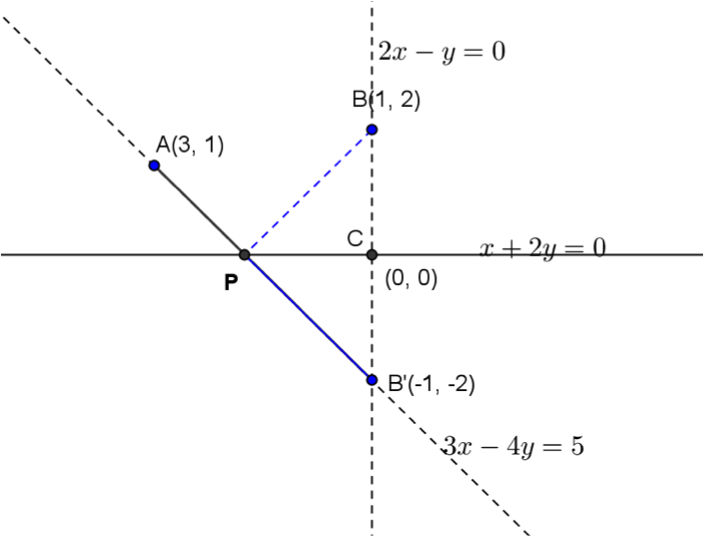
有一光線過點 \(B(1,2)\)，射到直線 \(L:x+2y=0\) 上一點 \(P\)，反射後經過 \(A(3,1)\)，
試求 \(\overline{PA}+\overline{PB}\) 之值。

解：先求 \(B\) 點對 \(L\) 的對稱點 \(B’\)，坐標為 \(B'(-1,-2)\)，此時 \(P\) 點為 \(\overleftrightarrow{AB’}\) 與 \(L\) 的交點，\(\overline{PA}+\overline{PB}=\overline{PA}+\overline{PB’}=\overline{AB’}=5\)

在問題情境中的光的反射，亦可改成粒子的碰撞反射，觀念是一樣的。

例題5
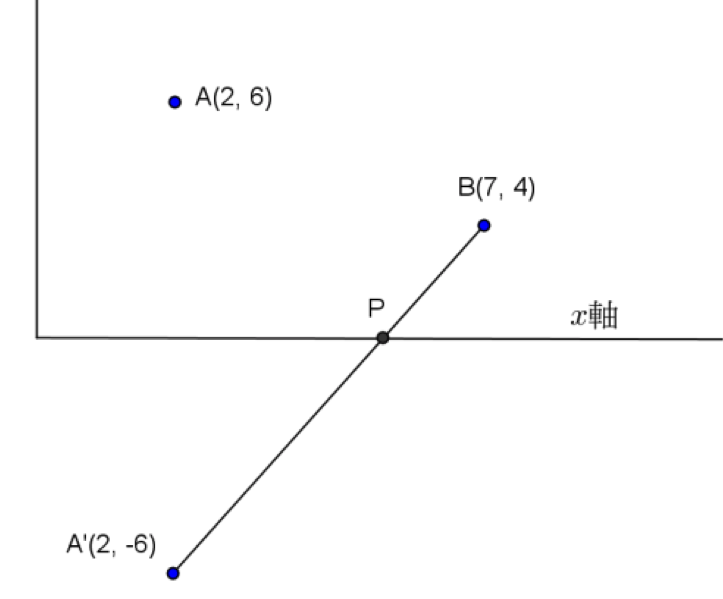
在撞球桌面上設立坐標系統，以檯邊為兩坐標軸，一球從坐標平面上的點 \(A(2,6)\) 打出，
碰到 \(x\) 軸的檯邊 \(P\) 點再折向撞擊到 \(B\) 球，已知 \(B\) 球坐標為 \((7,4)\)，則 \(P\) 點坐標為何？

解：先求得 \(A(2,6)\) 對 \(x\) 軸的對稱點 \(A'(2,-6)\)，連 \(\overleftrightarrow{A’B}\)，方程式為 \(2x-y=10\)，
\(\overleftrightarrow{A’B}\) 與 \(x\) 軸的交點 \(P\) 即為所求，\(P\) 點坐標為 \((5,0)\)。

最後，這一系列問題也可在空間坐標中來探討，只是情境中的直線變成空間中的平面而已，
亦即問題可改為：「在空間坐標中，給定兩點 \(A\) 與 \(B\)以及一平面 \(E\)，想要在 \(E\) 上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\)有最小值」，它的觀念與想法都是一樣的。