最短路徑問題
最短路徑問題
臺北市立西松高中 蘇惠玉教師
在數學III的直線單元中有這樣的問題:在坐標平面上,給定兩點 \(A\) 與 \(B\),以及一直線 \(L\),想要在 \(L\) 上找一點 \(P\),使得 \(\overline{PA}+\overline{PB}\) 有最小值。這個 \(P\) 點要怎麼找呢?我們先把 \(L\) 特殊化,從 \(x\) 軸上的點來考慮。
例題1
坐標平面上給定兩點 \(A(1,3),B(5,-1)\)。
在 \(x\) 軸上找一點 \(P\),使得 \(\overline{PA}+\overline{PB}\) 有最小值,\(P\) 點坐標為何?
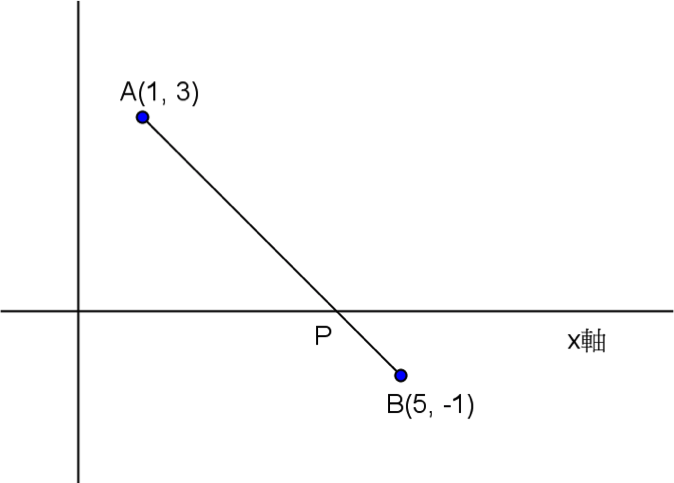
解:如圖,\(A,B\) 在 \(x\) 軸的異側。
由於兩點連線會與 \(x\) 軸相交,且兩點間直線距離最近,
因此當 \(P\) 點為 \(\overline{AB}\) 與 \(x\) 軸的交點時,此時 \(\overline{PA}+\overline{PB}\) 有最小值。
因為 \(\overleftrightarrow{AB}\) 的方程式為 \(x+y=4\),故與 \(x\) 軸的交點為 \(P(4,0)\),
此時所求最小值為 \(\overline{AB}=4\sqrt{2}\)。
由例題1可知,當 \(A,B\) 在所給直線 \(L\) 的異側時,
所要找的 \(P\) 點即為 \(\overleftrightarrow{AB}\) 與 \(L\) 的交點。
那麼當 \(A,B\) 都在 \(L\) 的同側時,要如何找到 \(P\) 點呢?
