弧度

弧度 (Radian)
國立屏東高級中學數學科楊瓊茹老師/國立臺灣師範大學數學系洪萬生教授責任編輯

「為什麼要將度換成弧度？」筆者總是會碰到一、兩位好學的學生一臉困惑的追問著。度度量（degree）轉換成弧度量（radian）對一般高中生而言較不易接受， 即使學生已經能習慣性地按「\(180^\circ=\pi\) 弧度」單位換算，但是，對於弧度的概念可能是模糊不清的，尤其 \(\pi\) 本身是個無理數卻又能表示角的大小，學生在直覺上不易理解。

其實，弧度量是一種用弧長來表示角的大小的方法，定義如下：

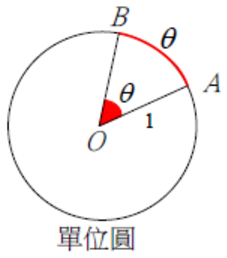
設 \(\angle AOB\) 為單位圓的圓心角，所對應的圓弧 \(AB\) 的長度為 \(\theta\)，規定

1. \(\angle AOB\) 的大小用圓弧 \(AB\) 的長度來表示，
2. 角的度量單位稱為弧度，弧度兩字可省略。

即 \(\angle AOB=\theta\) 弧度。

那麼，當圓弧 \(AB\) 長等於半徑 \(1\) 時，\(\angle AOB=1\) 弧度。而半圓的弧長為 \(\pi\)，所以，對應的圓心角為 \(\pi\) 弧度，即 \(180^\circ=\pi\) 弧度。因此，度與弧度之間的換算關係為：

\(1 \text{弧度} =\displaystyle(\frac{180}{\pi})^\circ\approx 57.2958^\circ\)

\(1^\circ=\displaystyle\frac{\pi}{180} \text{弧度} \approx 0.01745\) 弧度

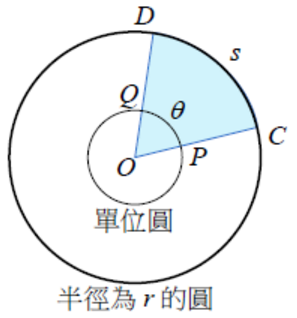
若圓的半徑為 \(r\)，圓弧 \(CD\) 長為 \(s\)，圓弧 \(PQ\) 長為 \(\theta\)，

則 \(\displaystyle \frac{s}{r}=\frac{\theta}{1}\)，即 \(\displaystyle\angle COD=\theta=\frac{s}{r}\)

也就是說，與半徑等長的圓弧所對應的圓心角為 \(1 \text{弧度}\)。

如此一來，角的大小可以用實數來表示，從而三角函數視為實數與實數之間的對應關係，便可在 \(x-y\) 平面上描繪出三角函數的圖形。

相較於度度量，弧度量的優點是讓數學公式變得簡潔（參見下表度度量與弧度量的比較），公式中少掉常數倍 \(\displaystyle\frac{\pi}{180}\)。尤其在微積分中，從 \(\displaystyle\lim_{x\to \infty}\frac{\sin x}{x}=1\) 逐步推導出的許多數學理論都是採用弧度量，奠定弧度量無可取代的地位。

所以，「弧度」不僅是另一種角的度量單位，可與「度」單位換算。更重要的是， 它能將數學公式化繁為簡，此一優點在微積分中充分展露無遺。

至於弧度何時成為角的公認度量單位，歷史並不久遠。1714 年，英國數學家羅傑‧寇茲（Roger Cotes, 1682~1716）用弧度的概念而不是度（degree）來處理相關問題，他認為弧度作為角的度量單位是很自然的。

1748 年，歐拉（Leonhard Euler, 1707~1783）在他的名著《無窮微量分析引論》（Introduction in analysin infinitorum）中主張用半徑為單位來量弧長，設半徑等於 \(1\)，\(\frac{1}{4}\) 圓周長是 \(\frac{\pi}{2}\)，所對的圓心角的正弦值等於 \(1\) 可記作 \(\sin\frac{\pi}{2}=1\)。

但是，他們都沒有使用radian這個名稱。英文的radian一詞第一次出現在印刷品中，是在1873年愛爾蘭工程師湯普遜（James Thomson,1822~1892）於伯斯發特的女王學院（Queen’s College in Belfast）所出的試題中。radian是由radius（半徑）與angle（角）兩字合成。

radian中文曾譯為「弳」，弳是弧與徑兩字合成。直到1956年，在中國科學院出版的《數學名詞》中，才正式定名為「弧度」。

參考資料

1. George B. Thomas, Jr / Ross L. Finney (1996). Calculus and analytic geometry-9th ed.
2. 毛爾著、胡守人譯 (2000).《毛起來說三角》，台北：天下文化。
3. 梁宗巨 (1998).《數學歷史典故》，台北：九章出版社。
4. http://en.wikipedia.org/wiki/Radian
5. http://fermatslasttheorem.blogspot.com/2007/12/roger-cotes.html