對數表的製作(Constructions of Logarithmic Tables)
對數表的製作(Constructions of Logarithmic Tables)
國立臺灣大學數學系曹亮吉教授責任編輯
球面三角學也有正弦律及餘弦律,類似於平面三角學的,天文學家常用它們來做計算,而要面臨兩個多位數相乘或相除的問題。為了解決乘除的問題,數學家首先想到三角學裡的積化和差公式,像是 $$\cos{A}\cos{B} =\frac{1}{2}{(\cos{(A+B)} + \cos{(A-B)})}$$。譬如要算 $${406.7} \times {87.46}$$,則先查表得 $$\cos{66^\circ} \approx 0.4067 $$,$$\cos {29^\circ} \approx 0.8746$$,因此
$$\begin{array}{ll}406.7 \times 87.46 &= 10^5 (0.4067 \times 0.8746) \approx 10^5 \cos{66^\circ}\cos {29^\circ}\\&=10^5 \times \frac{1}{2} (\cos{95^\circ}\cos {37^\circ} \approx 10^5 \times{1}{2}(-0.0872+0.7986)\\&= 10^5 \times \frac{1}{2} \times 0.7114 = 35570\end{array}$$
以上主要是查表及加減計算,不過還是要有相當的過程。於是數學家想到把任何數表成為 $$10$$ 的指數次方,而任何兩個這樣的數 $$10^a$$、$$10^b$$ 相乘或相除,就得 $$10^{a+b}$$ 或 $$10^{a-b}$$。$${a}$$ 就稱為 $$10^a$$ 的(常用)對數。化乘除為加減就是對數的主要功能。
現代的對數表是利用對數函數的泰勒級數來製作的,但十七世紀初發明對數時,還不知道這樣的方法。為了製作對數表,得先計算 $$10$$ 的一再平方根,得值如下表:
今以 $$\log{2}$$ 為例,說明求其值的方法:
$$2$$ 介於 $$10^{\frac{1}{2}}$$ 與 $$10^{\frac{1}{4}}$$ 之間;以 $$10^{\frac{1}{4}}$$ 除 $$2$$,得商$$ x_1 =1.1246…$$,即 $$2 = 10^{\frac{1}{4}}\times x_1$$。
用同樣的方法處理 $$x_1$$,得 $$ x_1 = 10^{\frac{1}{32}} \times {x_2}$$,$${x_2}=1.04659…$$。
處理$${x_2}$$,得 $${x_2} =10^{\frac{1}{64}} \times {x_3}$$,$${x}_3=1.00961$$…。
處理$${x_3}$$,$$ x_3 = 10^{\frac{1}{256}} \times {x_4}$$,$${x}_4=1.00450$$…。有必要的話,可以繼續往下做。
把 $$2$$、$$ x_1$$、$$ x_2$$、$$ x_3$$、$$ x_4$$ 串起來,就得
$$\begin{array}{ll} 2&=10^{\frac{1}{4}}\times x_1=10^{\frac{1}{4}}\times 10^{\frac{1}{32}}\times x_2=10^{\frac{1}{4}}\times 10^{\frac{1}{32}}\times 10^{\frac{1}{64}}\times x_3\\&=10^{\frac{1}{4}}\times 10^{\frac{1}{32}}\times 10^{\frac{1}{64}}\times 10^{\frac{1}{256}}\times x_4\end{array}$$
由於 $$x_k$$ 愈來愈小,會趨近於 $$1$$,所以 $$2$$ 寫成為 $$10$$ 的指數,
其指數要為 $$\frac{1}{4} + \frac{1}{32} +\frac{1}{64}+ \frac{1}{256}+…$$;
如果算到 $$\frac{1}{256}$$,則和為 $$\frac{77}{256}$$,即 $$\log{2} \approx \frac{77}{256}$$ ($$\approx$$ 0,3)。
一言以蔽之,把指數表成為 $$2$$ 進位的小數,這就是最初製作常用對數表的方法。


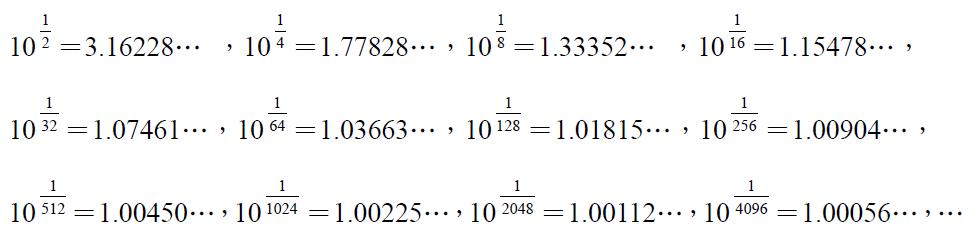
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
