對數函數（Logarithmic function）

對數函數（Logarithmic function）
國立北門農工職業學校數學科李建宗老師/國立台灣師範大學數學系洪萬生教授責任編輯

當自變數 $$x$$ 被放置在以 $$a$$ 為底的對數所表示出來的函數，我們便函這個函數為以 $$a$$ 為底的對數函數，數學符號就以 $$y=\log_ax$$ 表示之，其中，$$a$$ 是大於零且不等於 $$1$$ 的正實數，$$x$$ 是大於零的正實數。

$$y=\log_ax$$ 等價於 $$x=a^y$$，所以你就可以發現他和指數函數 $$y=a^x$$ 中，$$x$$ 和 $$y$$ 的角色已經對調了。也正因如此，在指數函數考慮底數 $$0<a<1$$ 和 $$a>1$$ 圖形會有不同性質的呈現，那對數函數將底數 $$a$$ 作相同考量時，是否也會有類似情況呢？那指數函數討論的遞增和遞減特性，在對數函數是否也有一樣的呈現？那凹口的情況又會變化如何？對數函數是否也和指數函數一樣恆過一定點呢？那指數函數有一漸進線為 $$x=0$$，那對數函數和指數函數，在 $$x$$ 和 $$y$$ 角色互換後，其漸進線會是 $$y=0$$ 嗎？那指數函數和對數函數之間的關係又是如何呢？等特性，都是我們下面要探討了。

在對數函數中，底數 $$0<a<1$$ 可畫出 $$g(x)$$，如下圖（一）；而底數 $$a>1$$ 可以畫出如 $$f(x)$$。而 $$\log_ax$$ 和 $$\log_{\frac{1}{a}}x~(a>1)$$ 圖形和指數函數 $$y=a^x$$ 和 $$y=(\frac{1}{a})^x~(a>1)$$ 一樣會有對稱的情況產生，只不過在對數函數對稱軸換成 $$x$$ 軸。

而遞增和遞減情況，則當 $$y=\log_ax~(a>1)$$ 情況呈現遞增，而 $$y=\log_ax~(0<a<1)$$ 是遞減，也就是說當底數條一樣下，指數函數和對數函數有相同遞增遞減情況。而凹口情況，在指數函數不管底數如何都是呈現凹向上，而在對數函數，當 $$0<a<1$$ 時，凹向上也就是對數函數是凸函數，但 $$a>1$$ 時，卻呈現出凹向下，也就是凹函數。對數函數依然會恆過一定點 $$(1,0)$$，也就是代表著 $$1$$ 是任何正實數的 $$0$$ 次方。

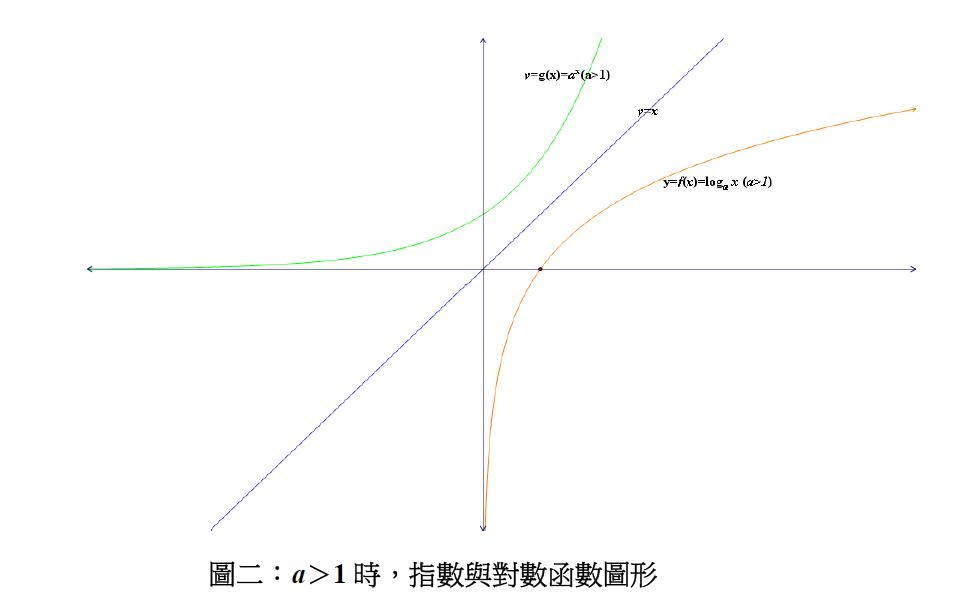
對數函數也如同指數函數一樣有一條很靠近軸的漸近線，只不過對數函數很靠近軸的漸近線為 $$x$$ 軸。那對數函數 $$y=f(x)=\log_ax$$ 等價於 $$x=a^y$$，而指數函數為 $$y=g(x)=a^x$$ 這種 $$x$$ 和 $$y$$ 在函數角色互換的情況，在數學上便有這種 $$f(g(y))=y$$ 且 $$g(f(x))=x$$ 的特性且其對稱軸也在 $$y=x$$ 線上，而我們就稱此兩函數互為反函數，而指數函數和對數函數正符合這種情況。

而反函數概念，在這裡便可以呈現出 $$a^{\log_ax}=x$$ 的公式，像這種情況表示式，便是指數函數和對數函數由反函數而來的一種數學符號表徵意義的呈現。而下圖（二）和（三），借由圖形直觀上意義，讓各位讀者更能了解圖形的在 $$x$$ 和 $$y$$ 角色互換的意義。

圖三：$$0<a<1$$ 時，指數與對數函數圖形