基態 (Ground State)
基態 (Ground State)
國立臺灣大學物理所羅雅琳
根據量子理論,一個系統的能量可能是離散的,而非如古典物理所述是連續的。例如著名的氫原子,其外圍繞核運動的電子之能量便是離散的。我們把能量是離散的這個特性稱為能量的量子化(quantization)。該系統各個離散的能量所對應的狀態稱為一個能階(energy level),而能量的最低值所對應的能階稱為基態。我們通常可以用一組數字(稱為量子數,quantum number)去描述一個能階。
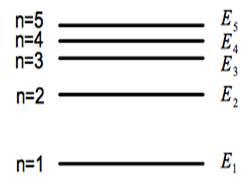
當系統的尺度(例如氫原子的直徑)與系統特徵長度(例如繞氫原子核運動的電子之物質波波長)相當時,量子化的現象通常會比較顯著。如圖一所示系統被量子化後,其各能階所對應的能量 $$E_n$$ 便是被量子數 $$n$$ 所描述,而最低能量 $$E_1$$ 所對應的量子態便是所謂的基態。
為了更瞭解何謂基態,我們首先來考慮一個簡單的例子:簡諧振子(simple harmonic oscillator)。根據計算,它的基態能量並不是零!換言之,在量子論中,簡諧振子永遠都在振動,而這和古典物理中認為簡諧振子可以處於完全不動的靜止狀態是很不同的。簡諧振子的基態能量有時稱為零點能(zero-point energy)。
接下來考慮一個比較複雜的系統:晶體概括性來說,晶體是由原子週期性排列而成,而原子我們可以用一個極為簡單的模型來描述它,也就是原子是由原子核及繞其運動的電子所組成,電子帶負電而原子核帶正電,因此總體來說原子為電中性。換句話說,晶體是由許多的電子及原子核所組成,而原子核在晶體中呈現週期性排列,因此我們可以把它想像成週期性位能井(potential well)。考慮許多電子在一個週期性位能井裡的運動,這是個複雜的物理問題,因此我們把它簡化成一個電子在一維無窮位能井裡[1]。此時電子的能量為
$$\displaystyle E_n=\frac{n^2h^2}{8mL^2}$$
$$n=1,2,3…$$,其中 $$m$$ 為電子的質量,$$L$$ 為無限位能井的寬度,而 $$h$$ 為普郎克常數(Plank constant)[3]。再一次,我們看到電子的基態能量並不是零,所以它也有零點能。
在量子場論(quantum field theory)或多體物理(many-body physics)中,我們又將基態稱之為真空態(vacuum state)。多體問題顧名思義便是考慮多個粒子交互作用的問題,因此只要非簡單的單粒子或雙粒子系統,我們都可以將其想成多體系統,而因為前述晶體是由多個電子及多個原子核組成,因此討論晶體的問體便是多體問題。然而真空態並不是指系統是“空”的狀態,也不是指所有粒子都不動(因為會有零點能),這名詞只是指一個多體系統的基態。在凝態物理(condensed matter physics)中,我們最常討論的便是多體系統處在真空態的物理特性,這是因為對於許多應用來說,處在基態的系統很穩定[4],且系統通常偏離基態不遠。
最後我們要討論一個重要的概念—簡併。當不同的量子態所對應的能量均相同時,我們稱之為簡併(degeneracy)。有些系統的基態具有簡併,這對於研究該系統在低溫時的熱學性質很重要,因為此時熱擾動很微小,系統基本上是處於基態,而根據熱力學,系統的熵(entropy)與簡併態的數目有密切關係[5]。
參考資料:
[1] Stephen Gasiorowicz, Quantum Physics, Wiley(2003)
[2] David J. Griffiths, Chapter 1, Introduction to Quantum Mechanics, Prentice Hall (2004).
[3] David Halliday, Robert Resnick, and Jearl Walker, Fundamentals of Physics Extended, Wiley(2013)
[4] Henrik Bruus and Karsten Flensberg, Many-Body Quantum Theory in Condensed Matter Physics: An Introduction,Oxford University Press (2007)
[5] R. K. Pathria and Paul D. Beale, Statistical Mechanics, Elsevier Ltd (2011)
[6] Steven T. Bramwell and Michel J. P. Gingras, Science 294 1495 (2001)


 前一篇文章
前一篇文章 下一篇文章
下一篇文章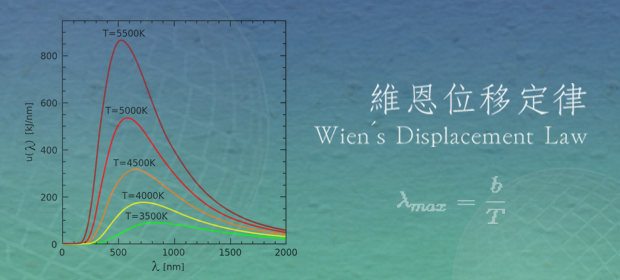 維恩位移定律
維恩位移定律  柯爾磁光效應
柯爾磁光效應 
