量子化

受激態(Excited State)
國立臺灣大學物理所羅雅琳

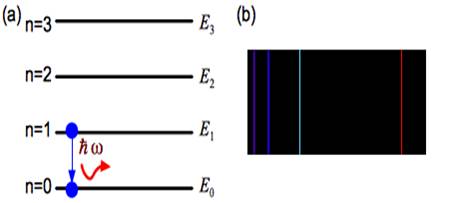
根據量子理論，一個系統的能量可能是離散的，而非如古典物理所述是連續的。我們把能量是離散的這個特性稱為能量的量子化(quantization)。該系統各個離散的能量所對應的狀態稱為一個能階(energy level)。我們通常可以用一組數字(稱為量子數，quantum number)去描述一個能階。當能量被量子化後，所有的量子態除了最低量子數所對應的基態（參見｢基態」條目）外，皆可稱之為受激態。如圖一 (a)所示，系統被量子化後，其各能階所對應的能量E_n 便是被量子數n所描述，而除了n=0的最低能量態外，其他所對應的量子態便是所謂的受激態。

圖一、(a)量子化能階圖。在量子化的圖像下，被描述的物理量與古典的連續量不同，取而代之的是用離散的量子數n來描述之，而En是用來描述量子化後能量。藍色表示粒子由受激態放出特定能量ℏω的光子回到基態。(b)氫原子發射譜線。（作者提供）