【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數
蕭維翰
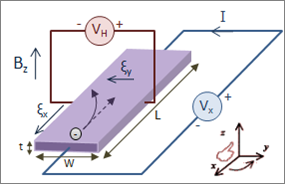
在前一篇筆者討論了整數的量子霍爾效應，也就是實驗中測得電導率的xy分量為電荷平方除以普朗克常數的整數倍。我們雖然沒有篇幅涵蓋實驗上所看到現象的所有必要物理概念，但至少有一個很概略的圖像：整個系統像一個公寓，公寓的樓層叫蘭道階，愈底層的公寓房租（能量）愈低，所有的電子便從第一層公寓築起，並且電子遵循庖立不相容原理（Pauli exclusion principle）所以一間房間只能住一個電子，實驗上這些整數對應到住滿的蘭道階的階數。[1]
【物理世界】量子霍爾效應（一）：塵埃中洗滌出的整數
蕭維翰
真的要寫量子霍爾效應，可以寫好幾本書，要從最尖端的進展切入，也會讓讀者摸不著頭緒，這邊我分稿從歷史的起源開始，並只挑一些聽起來真的可以令所有人驚訝的面向。
圖一：霍爾效應的實驗圖示，原本往 x 方向流的電賀受到磁場的影響在 y 方向也形成電壓，變成實驗上可以測量的霍爾電壓, credit: wikipedia
筆者儘管基於工作很常算數學，但上大學後幾乎不常親自動手做數字計算了。前幾個月我在電腦上送出一個滿複雜的積分，幾秒後我得到
\(\displaystyle\frac{-12.56637062125499}{4\pi}\)
不知道讀者們平常做算術的頻率如何，在作業中遇到這種數字會不會覺得很沮喪？分子那一串數字已經無跡可尋，何況底下還除一個 \(4\pi\)？然而有趣是，在電腦有效的位數下，這個組合其實跑出了── \(-1.00000000000000\)
雷射科學
陳勁豪
諾貝爾獎委員會於10月2日公佈了2018年的諾貝爾物理學獎的得主，分別是美國貝爾實驗室的Arthur Ashkin，法國巴黎綜合理工學院（École Polytechnique）的Gérard Mourou與加拿大滑鐵盧大學的Donna Strickland，以表彰他們在雷射科學上的突破性貢獻。
2018年諾貝爾物理學獎一共分為兩部份。第一部份頒給了由Arthur Ashkin所發明的光學鑷子（又稱光鉗）與光學鑷子與在生物系統上的應用。第二部份由Mourou與Strickland分享，以表彰他們所發明的產生高強度超短光學脈衝的方法。
電導率、弱局域化、與量子混沌（下）
蕭維翰
在上文中我們提及，物質波間的干涉會減弱系統的電導率，在本文中我們討論混沌現象（Chaos）[1]如何對這個減弱這個局域化的效應。
回顧前文，我們對於計算固態系統中電導率的方法稍作了討論，指出 Drude 圖像給出古典的計算結果。然後我們討論次一階的量子修正，說明在某些路徑上傳遞的物質波可以建設性干涉，放大粒子在運動時回到原點的機率，等效而言增強電阻、削弱電導，此現象稱為弱局域化（weak localization）。
電導率、弱局域化、與量子混沌（上）
蕭維翰
理論物理學的目的是為物理現象提供一些定量的描述。也因此一個完整的物理理論，應該能計算一些可觀測的物理量。基於人類對電磁現象的掌握，在可測量的一系列物理量中，電阻率（resistivity），或者是它的倒數，電導率（conductivity），大概是最直接的對象了，也因此，本文想趁機談談在一些問題中，物理學家如何從理論模型中得到電導率，而又有哪些因素會影響電導率。
電磁對偶（S-Duality）與歐姆定律（下）
蕭維翰
本文中我們以一個幼稚園版本的例子說明電磁對偶性如何幫助我們計算材料的電導率。
本圖為作者提供
在上文中筆者闡述了想解決的問題，也就是電阻 / 電導的計算，並透過費曼圖的角度嘗試去說服讀者這是個困難的問題，接著也複習了電磁對偶性，並深入一點點，探討在什麼情況下它才是個不無聊的性質。
長話短說，我們需要一個沒有電荷、電流的空間，在邊界上有一個允許有電荷、電流的薄膜。
旋轉的玻色愛因斯坦凝聚態
蕭維翰
圖一：旋轉的 BEC 中的漩渦和真實的漩渦
高中的物理課程中，我們學習動量、角動量，用這兩個量來量化一個物件平動狀態以及轉動的狀態。儘管大多數人在大學後不會再接觸更進階的物理課程，但事實上就描述運動狀態而言，也沒有更多新的物件了。
物理學的理論描述是盡量得跟實驗呼應的，也因此，即便是今日大如強子對撞機的尖端實驗，源頭的想法也都是想藉由動量、角動量等在交互作用的前後關係，去獲得物理資訊。
本文就來略談，當我們轉動一個流體，更精確地說，一個玻色愛因斯坦凝聚態（Bose-Einstein Condensate），什麼事情會發生。
路徑積分與費曼圖（下）
蕭維翰
連結：路徑積分與費曼圖（上）
1965 年的諾貝爾獎得主，由左至右為 Tomonaga, Schwinger, and Feynman, credit: Photos: Copyright © The Nobel Foundation “The Nobel Prize in Physics 1965”. Nobelprize.org. Nobel Media AB 2014.
在前文中筆者指出，路徑積分在發明之際主要是作為另一種計算給定物理過程所對應躍遷振幅的方法，費曼圖是物理過程的圖像表示，當畫出一個費曼圖，原則上我們能夠將它拆解成一些小過程，而每個小過程可由費曼規則對應到某個數學式，也就是我們所求的答案。
在費曼的工作之前，儘管人們已經知道了在量子場論中進行這種計算的方法，但當時，這幾乎是只有最頂尖的理論物理學家才能進行的計算，而今任何一個研究所水平的物理本科生幾乎都能進行最簡單的微擾理論計算。
路徑積分與費曼圖（上）
蕭維翰
本次費曼專題筆者希望透過兩篇文章談論費曼的路徑積分與費曼圖，作為費曼科學工作的代表。而本文將側重於路徑積分，並在結尾引出費曼圖。
但在科學開始之前，筆者必須承認，一直以來，我認為談論費曼的科學工作不是簡單的事。困難處不在於那些科學技術上的深澀，反在於它們的基礎性與普世性，在沒有獨樹一幟的新見解前，這個世界需不需要多一篇介紹費曼學術成就的科普文？
筆者相信在 CASE 的多年耕耘下，讀者們對於路徑積分或多或少都有所耳聞。科普界亦已有許多談論路徑積分的文章，絕大多數都會以光子或電子的雙狹縫干涉實驗為物理動機進行說明，以一個科學工作者的角度來看，這的確不失為好的介紹方式——首先提出實驗可想見實現的物理情境，接著嘗試利用物理直覺猜測可能的結果，再以意料之外的真實現象誘使讀者思考，最後說明迄今人類對於此問題的理解，並抽象化成為整個量子理論的指導原則。