能量

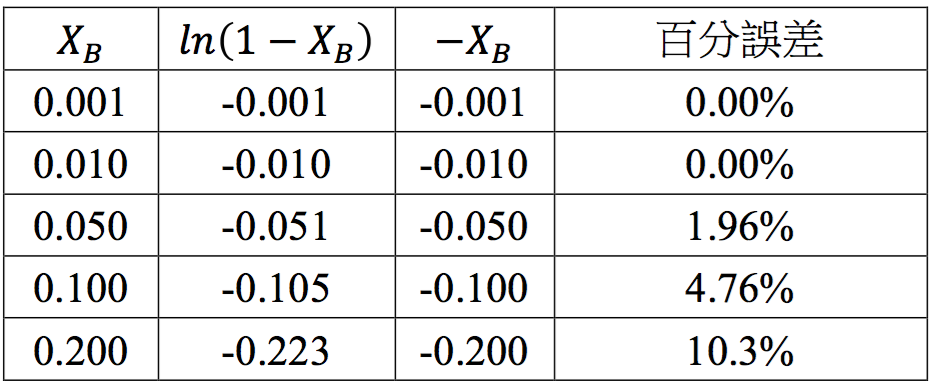
利用熱力學公式繪製二氧化碳的相圖（下）
國立臺灣師範大學化學系兼任教師邱智宏

連結：利用熱力學公式繪製二氧化碳的相圖（上）

(一)、繪製固-液相的共存線

在熔點時 $$\Delta S_m=\frac{\Delta H_{fus}}{T}$$，其中 $$\Delta H_{fus}$$ 為二氧化碳的熔化熱。將其代入 $$(2)$$ 式

 $$\displaystyle \frac{dp}{dT}=\frac{\Delta H_{fus}}{T\cdot \Delta V_{fus}}~~~~~~~~~(3)$$

兩邊積分 $$\int_{p^*}^{p} dp=\int_{T^*}^{T}\frac{\Delta H_{fus}}{T\cdot \Delta V_{fus}}dT$$，

若將 $$\Delta H_{fus}$$ 和 $$\Delta V_{fus}$$ 視為定值且 $$\int_{T^*}^{T} \frac{dT}{T}=\ln(\frac{T}{T^*})$$，則

$$p=p^*+\displaystyle\frac{\Delta H_{fus}}{\Delta V_{fus}}\ln(\frac{T}{T^*})~~~~~~~~~(4)$$

式中二氧化碳的熔解熱為 $$\Delta H_{fus}=8.33~kJ/mol$$，至於 $$\Delta V_{fus}$$ 只要查出固相及液的密度，便能計算出其莫耳體積的差為 $$28.94~cm^3/mol$$。

利用熱力學公式繪製二氧化碳的相圖（上）
國立臺灣師範大學化學系兼任教師邱智宏

高中化學課程介紹純物質的相圖(phase diagram)時，均以大家耳熟能詳的「水」開始，探討其在不同溫度、壓力下的狀態變化。究其原因主要為水對生物體及自然界至為重要，而且在日常生活中每天都會接觸到，其三態的變化也易以觀察。

唯，水的相圖並非常態，而是少數的例外，大多數物質的相圖和水的長相不同。另外，有些純物質的某些狀態在常溫、常壓下並不存在，學生可能誤以為無此狀態，因此若能以二氧化碳作為介紹常態相圖的起點，不失為一種變通的方式。

沸點上升法求分子量的限制（下）
國立臺灣師範大學化學系兼任教師邱智宏

連結：沸點上升法求分子量的限制（上）

三、$$\ln(1-X_B)=-X_B$$誤差的探討

$$\ln(1-X_B)=-X_B$$ 成立的條件為 $$1\gg X_B$$，即溶質的莫耳分率遠小溶劑，為一稀薄溶液方能適用。如果我們直接將不同莫耳分率的 $$X_B$$ 直接經由計算機求出 $$\ln(1-X_B)$$ 的值，並比較其大小，如表二所示。

表二 不同 $$X_B$$ 情況下，$$\ln(1-X_B)$$ 和 $$-X_B$$ 的百分比誤差

沸點上升法求分子量的限制（上）
國立臺灣師範大學化學系兼任教師邱智宏

一般而言非揮性溶質的分子量可依 $$\Delta T=K_bm_B$$，的公式來求出。然而現今的實驗室鮮少使用此法求取物質的分子量，唯在教學上，基於依數性質的應用及探討，此部分的內容仍有其存在的必要。但是此法在使用上有一些限制，尤其僅適用於稀薄的溶液中，此點在一般課程內容中甚少提及，以下將此公式的推導及假設詳述一遍，以免遭到誤用。

一、沸點上升公式的推導

圖一 異相平衡中，B為非揮發性溶質，A為溶劑，A在氣相的化學能會等於其在液相的化學能

假設在理想溶液中，$$B$$ 為非揮發性(nonvolatile)溶質，$$A$$ 為溶劑如圖一所示，當系統達到平衡時，液相中 $$A$$ 的化學能（$$\mu_A(l)$$）會等於氣相中 $$A$$ 的化學能（$$\mu_A^*(g)$$），上標的 $$*$$ 代表其為純物質。

$$\mu^*_A(g)=\mu_A(l)~~~~~~~~~(1)$$

由熱力學的定律可知，相同狀況下，純溶劑的化學能永遠高於溶液的化學能，如下式所列，
其中 $$X_A$$ 代表溶劑的莫耳分率，其值小於 $$1$$，
故 $$\ln (X_A)<0$$。

$$\mu_A(l)=\mu^*_A(l)+RT\ln X_A~~~~~~~~~(2)$$

淺談電能儲存與液流電池(flow batteries)的最新發展
國立臺灣大學化學系名譽教授蔡蘊明

現代的社會高度倚賴能量，其中最大宗的能源來自於天然氣、石油、以及煤這些自然資源。大自然透過上千萬或億年孕育出這些資源，而人類卻在工業革命之後的這短短數百年，就已經將之消耗到產生資源耗竭的危機，這些資源的耗費隨伴產生的污染也同時增加了環境沈重的負荷。替代的核能，看似消耗的自然資源不多，但所產生的輻射污染物亦是燙手山芋，潛在的核安問題更是爭論的焦點。太陽能以人類的歷史時軸來看，可稱永續，但如何有效的進行能量轉換，仍須很多的研究。與水利和風力發電一般，這幾種型態的能源，堪稱靠天吃飯，另具有地域性和電力的不穩定性，對環境的影響也並非沒有爭議。

生質酒精燃料 （biomass alcohol fuels）
臺北市立第一女子高級中學二年級高偉家

在這個工業進步的時代，除了國際經濟依賴石油之外，燃燒石油所產生的溫室氣體也使環境加速汙染，因此，生質能源的使用愈發顯得重要。生質酒精也可稱為生物乙醇，是一種利用微生物將生質(biomass)中醣分發酵的酒精，分子式CH₃CH₂OH，雖與石化原料產生的乙醇相同，但原料的不同就造成了碳排放量的差異，生質一般為植物光合作用產生的含碳化合物，通常製造生質酒精的原料以甘蔗、玉米為主，其他也有大、小麥、燕麥、稻米、甜菜、高粱、木薯等，甚至於廢棄物如舊報紙、木屑等。