能隙

能隙 (Energy Gap)
國立臺灣大學物理學系 洪豪謙

能隙的概念是從能帶理論 (Band theory) 中發展的，這是二十世紀初量子力學確立以後，所發展的一套理論，迄今運用這個理論最廣泛的領域是半導體元件。

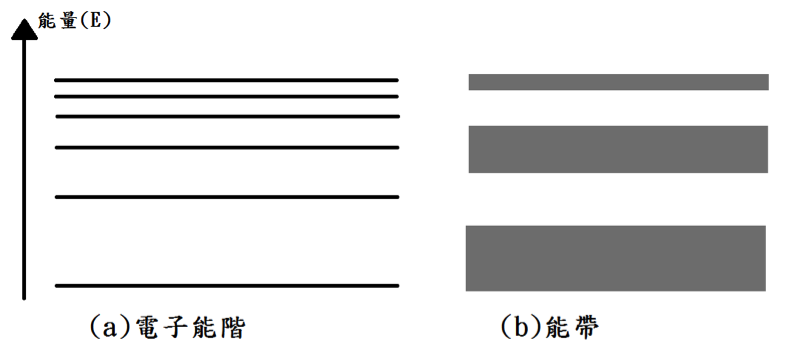
我們知道單電子的氫原子模型中，因為量子效應，造成電子的能階是不連續的，從一個能階跳到另外一個能階的吸收或是放出的能量必須是固定的，示意如圖一 (a)。如果現在我們考慮的是一個固體，也就是相當大量的原子規則地排列在一起，那麼我們也是一樣能夠看到這個不連續的狀況，但由於需要考慮到原子之間的交互作用、排列方式造成的位能差，甚至是電子跟電子之間也有交互作用，所以我們看到的不是一條一條的能階，而是好幾個「能帶」，也就是電子的能量能分佈於一個範圍內，如圖一 (b)。

圖一、(a) 電子能階 (b) 能帶。

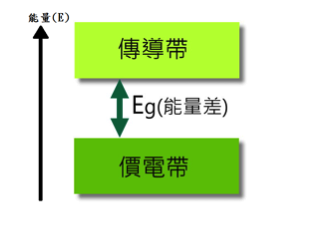
每個能帶之間都有個能量差，我們便稱之為能隙 (Energy gap)，在能隙之中電子是無法穩定存在的，所以這個區域也稱作禁帶 (Forbidden band)。在原子模型中，外層的價電子相對於其他內層電子通常有著更高的能量，也是最容易脫離原子束縛的電子。而在固體內部，每個原子所提供的價電子會組成在絕對溫度為零時（此定義請參考本文最末提及的「費米-迪拉克統計分佈」）能量最高的能帶，稱作價電帶 (Valence band)。若給予一個價電帶的電子大於能隙的能量，它有機會跳到能量更高的能帶「傳導帶 (Conduction band)」，如圖二表示。在傳導帶內的電子有足夠的能量能夠不被原子束縛住，而在固體內部自由移動，也造成了這個固體能夠導電，電子跳到傳導帶的同時會留下ㄧ個「電洞」在價電帶，這個電洞能在原子間自由移動，因此同樣具有導電的功用。

圖二、能帶圖，其中 Eg 是 Energy gap 的常用簡稱。（本文作者洪豪謙繪）

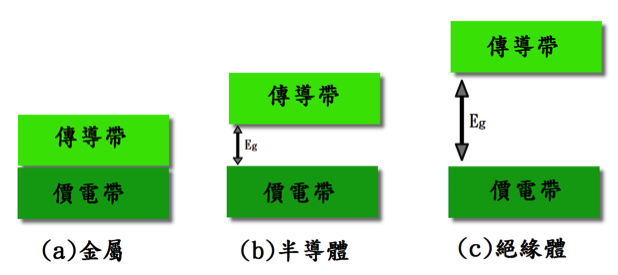
一個固體容不容易導電主要是看能隙的大小，大部分金屬的傳導帶跟價電帶有部份是重疊的或者之間的能隙極小，因此非常容易導電；絕緣體的能隙相當大 (> 4eV)，因此很難傳導電；半導體的能隙則介於導體與絕緣體之間，像是矽的能隙約為 1.12eV。能隙的差距如圖三表示。

圖三、金屬、半導體、絕緣體的能隙差距。（本文作者洪豪謙繪）

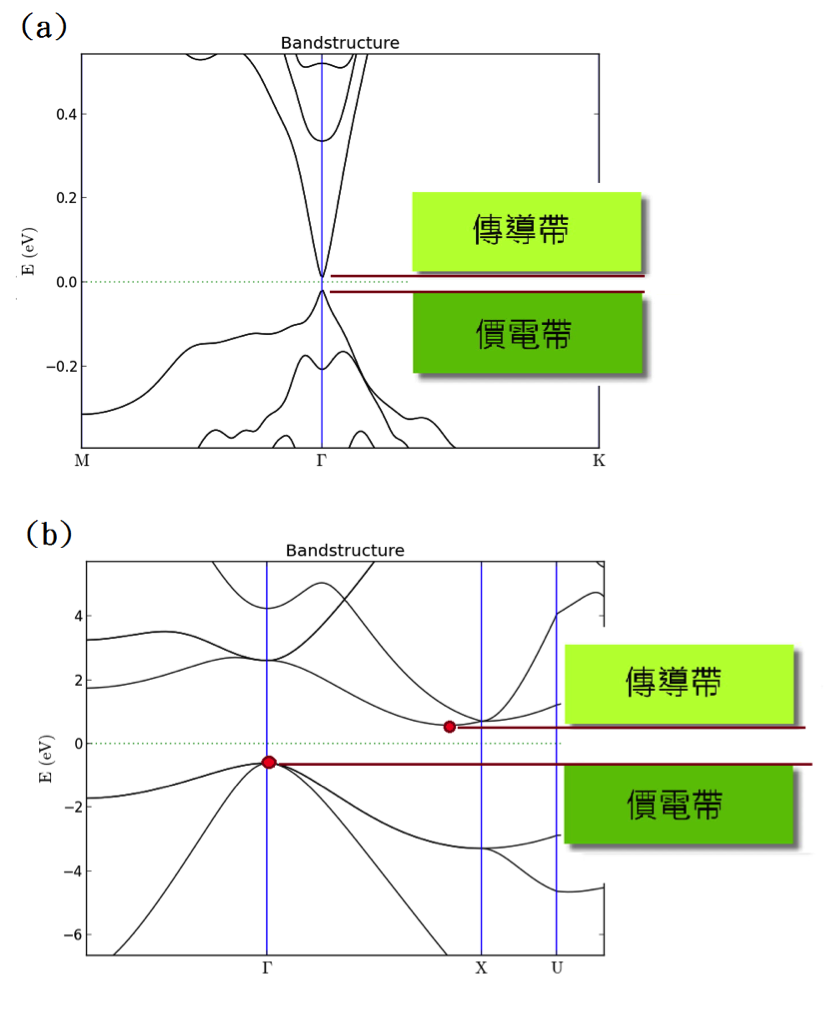
但實際上能帶的分佈其實並不是如圖一 (b) 所表示的這麼單純，我們要用到能帶結構 (Band structure) 來表現出最貼近實際的狀況，如圖四表示，能量跟電子的動量有著相當大的關係。

圖四、能帶結構（$$\mathrm{Bi_2Se_3}$$ 以及矽），橫軸代表電子不同的動量，縱軸則是對應於該動量之能階。（本文作者洪豪謙繪製）

圖四的縱軸為能量，橫軸可視為電子的動量，圖中 0eV 附近並沒有能帶經過，屬於禁帶，上下則分別屬於傳導帶及價電帶，0eV 是費米能階 (Fermi level)。(a) 直接能隙（本圖使用電腦軟體模擬，模擬材料為 3QLs Bi₂Se₃）(b) 間接能隙（模擬材料為矽）

能帶結構中，上半部以及下半部最接近的兩個點的距離就是能隙，圖四 (a) 屬於直接能隙 (Direct energy gap)。圖四 (b) 屬於間接能隙 (Indirect energy gap)，這個狀況下的電子若要以最小的能量跳到傳導帶，需要有其他機制改變電子動量才能達成。

最後要提到的是費米—迪拉克統計分佈 (Fermi-Dirac Statistical Distribution)，這是像電子這類遵守包立不相容原理 (Pauli exclusion principle) 的粒子必須遵守的分佈，其基本的想法是兩顆電子不能同時佔據同一個能態，但也不會每個能態都被電子填滿。經過數學推導後得到以下公式：

$$\displaystyle f(E)=\frac{1}{e^{(E-E_f)/kT}+1}$$

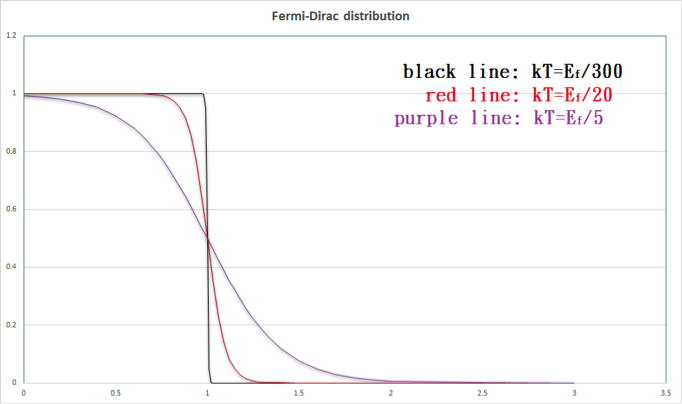
$$f(E)$$ 代表占據該能態的平均電子數，$$E$$ 是能量，$$E_f$$ 是費米能階 (Fermi level)，$$k$$ 是波茲曼常數，$$T$$ 是溫度。$$f(E)$$ 對能量作圖如下。

圖五、費米-迪拉克統計分佈。（本文作者洪豪謙繪製）

費米能階定義為在 0K 時電子具有最高能量的能階。簡單來說，熱平衡狀態下，大部分的電子存在於費米能階之下，只有一小部分的電子擁有的能量高於費米能階。費米—迪拉克統計分佈的重點是在說明溫度跟電子機率分佈也很大的關聯（圖五），溫度越高圖形越是平緩，溫度越低則是越陡峭。現在我們看圖四，會發現費米能階位於價電帶與傳導帶之間，若要有良好的導電性，則存在於價電帶的電子越多越好，也就是說需要大量電子的能量高於費米能階，所以在高溫下半導體的導電性是不錯的。相對來說，在低溫下只存在著少量電子和電洞協助導電，導電性較差。

參考文獻

1. Taur, Yuan, and Tak H. Ning. (2009). Fundamentals of Modern VLSI Devices (2nd ed.). Cambridge: Cambridge Univ. Press.
2. Griffiths, D. J. (2004). Introduction to Quantum Mechanics (2nd ed.).Prentice Hall.
3. Carter A. H. (2001). Classical And Statistical Thermodynamics. Cambridge Univ. Press.
4. Band Structure — Wikipedia. http://en.wikipedia.org/wiki/Electronic_band_structure