指數律(Exponentials)

指數律(Exponentials)
國立中央大學數學系單維彰副教授/國立中央大學數學系單維彰副教授責任編輯

 令 $$a$$ 為實數，$$n$$ 是正整數，$$a^n$$ 有具體的意義：$$a$$ 自己連乘 $$n$$ 次。現在我們要討論當指數是 $$0$$、負整數、分數、無理數時，次方計算的意義為何。

我們首先了解當指數為 $$0$$ 的意義是什麼？為了相容於自然數指數律中的加法律，我們希望 $$a^n\times{a^0}=a^{(n+0)}=a^n$$，所以規定：當 $$a\neq 0$$ 時，$$a^0=1$$。以前，數學的慣例是說 $$0^0$$ 無定義，但是越來越多的計算機軟體，採取 $$0^0=1$$ 的慣例。

當 $$a\neq{0}$$ 時，還是為了保持指數加法律：$$a^n\times{a^{-n}}=a^{n+(-n)}=a^0=1$$，所以規定 $$a^{-n}=\frac{1}{a^n}$$。這個規定也符合 $$10$$ 的次方性質：$$10^{-1}=0.1$$、$$10^{-2}=0.01$$、$$10^{-3}=0.001$$。例如 $$1~nm=\frac{1}{10^9}~m$$ 也可以寫成 $$1~nm=10^{-9}~m$$。

如上規定了以 $$0$$ 或負整數為指數的次方意義之後，我們將會發現，除了指數加法律以外，乘法律和分配律也都對 $$0$$ 或負整數的指數成立。

當底數是 $$0$$ 時，對任意實數 $$x>0$$，我們規定 $$0^x=0$$，而 $$0^{-x}$$ 無意義。所以，以下不再討論底數是 $$0$$ 的情況。

我們已經知道，對任意正數 $$0<a\in\mathbb{R}$$，$$a$$ 的 $$n$$ 次方根 $$\sqrt[n]{a}$$ 的定義為方程式 $$x^n=a$$ 的（唯一）正根。為使有理數指數仍具備指數乘法律，我們希望

$$\sqrt[n]{a}=a^p$$，而 $$(\sqrt[n]{a})^n=a^{np}=a$$，

因為 $$a=a^1$$，所以希望 $$n\times{p}=1$$，因此規定 $$p=\frac{1}{n}$$，也就是說：

當 $$a>0$$，規定 $$a^{\frac{1}{n}}=\sqrt[n]{a}$$

一般而言，當 $$p=\frac{m}{n}$$ 是有理數時，正數的 $$p$$ 次方定義如下：

$$a^{\frac{m}{n}}=(a^m)^{\frac{1}{n}}=\sqrt[n]{a^m}$$，$$0<a\in\mathbb{R}, m\in\mathbb{Z}, n\in\mathbb{N}$$

當指數進入非整數的範疇時，我們不討論底數為負數的情況。如上定義的有理數指數，將會保持整數指數的所有運算規則。

當指數是無理數時，我們需要極限概念，不能在此篇內完整說明。而現在的次方計算，全部透過指數函數與對數函數完成，也不能在此篇中完整說明。簡單地說，無理數總可以用有限小數當作估計值，而有限小數是有理數，所以可以用次方根的意義來計算無理數次方的估計值。

以 $$10^{\sqrt{2}}$$ 為例，因為 $$\sqrt{2}\approx{1.4}$$，而 $$1.4=\frac{14}{10}=\frac{7}{5}$$，求方程式 $$x^5=10^7$$ 之正根 $$\sqrt[5]{10000000}$$ 的近似值（用中間值定理或其他方法），得到 $$\sqrt[5]{10000000}\approx{25.1189}$$，所以 $$10^{\sqrt{2}}\approx{25.1189}$$。

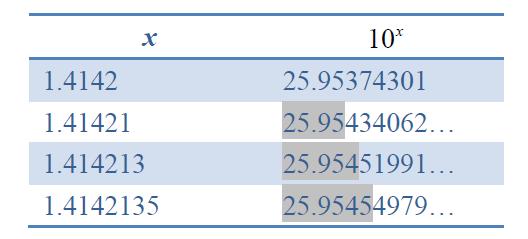
以上雖然算出來 $$10^{\sqrt{2}}$$ 的一個估計值，但是不知道有多準確？若我們希望得到準確到小數點下第四位的估計值，則必須將 $$\sqrt{2}$$ 的近似值準確度提升，並逐次觀察次方估計值的變化，直到某些位數不再隨著 $$\sqrt{2}$$ 近似值的準確度而改變，就能確定那些數字是正確的。例如，觀察以下表格，其中 $$x$$ 那一欄依序是 $$\sqrt{2}$$ 的近似值，而 $$10^x$$ 那一欄是用該近似值計算的 $$10^{\sqrt{2}}$$ 估計值。

右欄中灰色底的位數代表與精確度較低的 $$x$$ 相較之下仍相同的位數，這些數字不再隨 $$x$$ 的準確度改變，就能確定是和 $$10^{\sqrt{2}}$$ 相同的數字。因此我們可以確定 $$10^{\sqrt{2}}=25.9545…$$。若我們將這個列表無限延伸下去，$$10^{\sqrt{2}}$$ 的數值也能無限延伸下去。任意規定一個需要準確的位數（一個正整數的小數點下位數），這個可以無限延伸的表格，總有達到要求的時候。

透過極限觀念定義的實數指數，也都繼承了有理數指數的所有運算規則。

綜合以上所述，我們整理出一般的指數運算規律如下。

 $$\blacksquare$$ 底數 $$a$$ 為零時

指數 $$x>0$$ 時 $$0^x=0$$，$$0^{-x}$$ 無意義; $$0^0$$ 無定義

$$\blacksquare$$ 指數 $$x$$ 非整數時

不討論底數 $$a<0$$ 的情況

$$\blacksquare$$ 排除上述狀況後，指數計算對於所有實數 $$a, b, x, y$$ 皆符合以下規律：

$$\blacksquare$$ 指數加法律：$$a^x\times a^y=a^{x+y}$$
$$\blacksquare$$ 指數乘法律：$$(a^x)^y=a^{xy}$$
$$\blacksquare$$ 指數分配律：$$(a\times b)^x=a^x\times b^y$$

向前連結：自然指數與科學記號、冪函數、勘根定理、整數、有理數、實數、極限

向後連結：指數函數