實數
實數 (Real Numbers)
國立中央大學數學系單維彰副教授/國立中央大學數學系單維彰副教授責任編輯
讓我們先開宗明義地說明什麼「是」實數。在數線上任取一點 $${P}$$,它與原點 $${O}$$ 的線段長是數線之單位長的(唯一)倍數,記作 $$\overline{OP}$$,此數即為 $$0$$ 或正實數。若 $${P}$$ 即原點,則其坐標為 $$0$$;若 $${P}$$ 在原點右側(即數線的箭頭方向),令其坐標為 $$\overline{OP}$$;若 $${P}$$ 在原點左側,令其坐標為 $$-\overline{OP}$$。則實數的幾何看法是:
數線上任一點的坐標就是實數,它是正或負的單位長倍數。
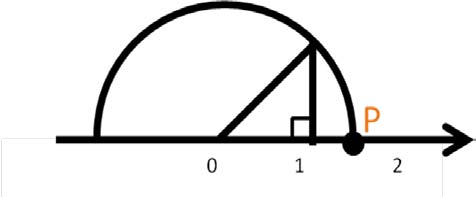
現在,讓我們沿著數線上畫出一個腰為單位長的等腰直角三角形,並以原點為其中一個頂點。如下圖。
以此三角形的斜邊為半徑,以原點 $${O}$$ 為圓心,畫出一圓交數線於兩點,其中一點在 $${O}$$ 的右側,令它是 $${P}$$ 點。可見 $${P}$$ 點確實在數線上,而根據畢氏定理 $$\overline{OP}= \sqrt{2}$$,所以 $$\sqrt{2}$$ 是一個實數。我們已經知道 $$\sqrt{2}$$ 不是有理數,所以,有理數雖然稠密,卻不能「佈滿」數線。有理數在數線上留下許多肉眼不能觀察,心靈卻能洞悉的空隙。數線上坐標不是有理數的點,其坐標就稱為無理數。例如 $$\sqrt{2}$$ 是一個無理數。
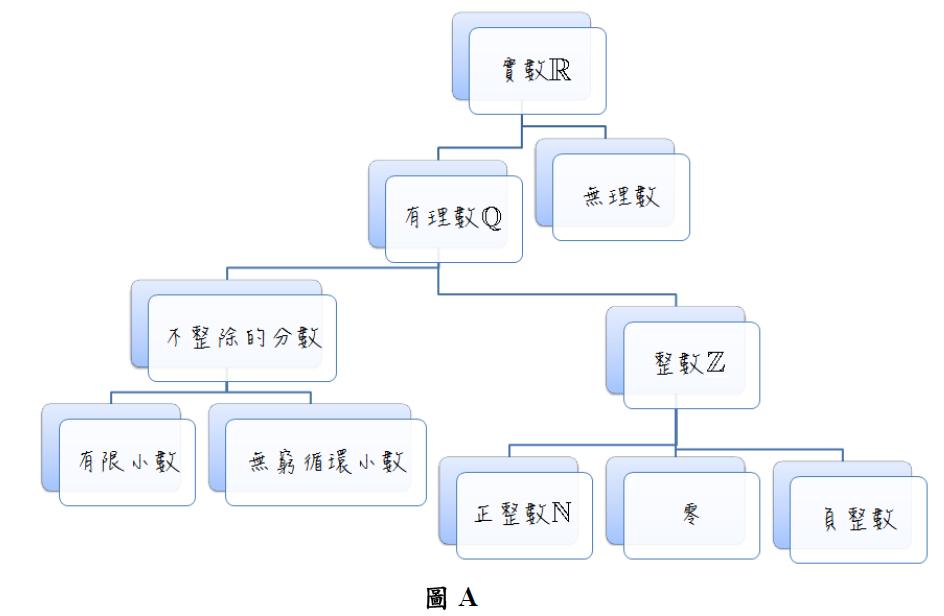
實數集合以 $$\mathbb{R}$$ 表示,所謂「$${x}$$ 是一個實數」也可以用 $${x}\in \mathbb{R}$$ 表示。從自然數開始不斷架構直至實數的概念後,我們便可以畫出一個實數家族圖,圖A。在這個圖上,下方的「數族」是上方的一部份,我們稱下方的是上方的子集合。例如正整數是整數的子集合,正整數也是有理數的子集合,記作 $$\mathbb{N} \subset \mathbb{Z}$$ 或 $$\mathbb{N} \subset \mathbb{Q}$$。
除非特別聲明,我們平常所說的「數」就是指實數。圖A中所有種類的「數」都在數線上,是實數的子集合。因為有著數線的模型,使得實數和它的所有子集合,都具備一個很特殊的性質,稱為三一律:
令$${a}$$、$${b}$$ 為實數,則 $${a}>{b}$$ 或 $${a}<{b}$$ 或 $${a}={b}$$ 三種關係必有一個且僅有一個成立。
這是因為,實數 $${a}$$ 與 $${b}$$ 各自是數線上某兩點 $${P}$$ 與 $${Q}$$ 的坐標。則 $${P}$$、$${Q}$$ 兩點在數線上的相對位置只能有以下三者之一:$${P}$$ 與 $${Q}$$ 重疊,$${P}$$ 在 $${Q}$$ 的右側,$${P}$$ 在 $${Q}$$ 的左側。因為我們規定 $${P}$$ 在 $${Q}$$ 的右側就是「$${a}$$ 大於 $${b}$$」,$${P}$$ 在 $${Q}$$ 的左側就是「$${a}$$ 小於 $${b}$$」,$${P}$$ 與 $${Q}$$ 重疊就是「$${a}$$ 等於 $${b}$$」,所以就是三一律了。
要將實數 $${x}$$ 用數字表示,必須先規定一個記數系統。就採用自然數和有理數所用的十進制。如果 $${x}$$ 是整數,我們已經知道該怎麼寫,所以不討論了。如果 $${x}$$ 不是整數,它一定在連續兩個整數之間:
$${n} \leq {x} < {n+1}$$,其中 $${n} \in \mathbb{Z}$$。
則 $$ 0 \leq {x}-{n} \leq {1}$$ 以十進制數字寫出來,是一個純小數 $${p}$$,所以 $${x=n +p}$$ 就得到 $${x}$$ 的十進制小數表示。現在,我們可以用數字來說明什麼「是」實數:
小數點下有任意多位數字的數值 $$\pm N.{b_1}{b_2}{b_3}{b_4}…$$,其中
$${N} \in \mathbb{N}$$,$${b_k} \in \{0,1,2,3,4,5,6,7,8,9\}$$,就是一個實數。
我們已經知道,當 $${x}$$ 的小數部分是有限小數或無窮循環小數時,$${x}$$ 是有理數;所有其他不循環的無窮小數都是無理數。正的實數稱為正數,負實數則稱為負數。
觀察十進制小數 $${p}= 0.416…$$ 在數線上的位置:
- 將 $$0$$ 到 $$1$$ 的區間等分十份,每份的長度是十分之一,
則 $$0.4 \leq {p} \leq 0.5$$,而 $${p}$$ 的十分位是 $$4$$。 - 將 $$0.4$$ 到 $$0.5$$ 的區間等分十份,每份的長度是百分之一,
則 $$0.41 \leq {p} \leq 0.42$$,而 $${p}$$ 的百分位是 $$1$$。 - 將 $$0.41$$ 到 $$0.42$$ 的區間等分十份,每份的長度是千分之一,
則 $$0.416 \leq {p} \leq 0.417$$,而 $${p}$$ 的千分位是 $$7$$。
讀者應該已經觀察出來,若
$$\displaystyle\frac{b}{10^n} \leq {p} < \frac{b+1}{10^n}$$,其中$${b} \in \{0,1,2,3,4,5,6,7,8,9\}$$,
則 $${p}$$ 的小數點下第 $${n}$$ 位的數字就是 $${b}$$。
應用上述十進制小數在數線上的意義,我們能夠用每次十等分的想法,決定無理數的在小數點下第一、第二、第三、第四…位的數字,稱為十分逼近法。以 $$\sqrt{2}$$ 為例,令數線上點 $${P}$$ 的坐標是 $$\sqrt{2}$$,根據 $$(\sqrt{2})^{2}=2$$ 之性質,我們以十分逼近法決定 $${P}$$ 點坐標的小數點下前三位的數字。
$$\blacksquare$$ 已知 $${P}$$ 點落於 $$1$$ 與 $$2$$ 之間,因此我們將 $$1$$ 到 $$2$$ 之間的切成十等份,其間九個等分點的坐標為 $$1.1$$、$$1.2$$、$$1.3$$、…、$$1.9$$。計算這九個數的平方,其結果列表如下。

由計算的結果看到,$$1.4^2 <2$$ 但是 $$1.5^2 > 2$$,所以 $$1.4<\sqrt{2} < 1.5$$,即 $${P}$$ 應該介於 $$1.4$$ 與 $$1.5$$ 之間。所以知道 $$\sqrt{2}$$ 的十分位是 $$4$$,亦即$$\sqrt{2}=1.4…$$。
如果我們的圖畫得足夠精確,則能夠在將上圖加上了新的刻度後,從放大鏡中看到下圖,顯示出 $${P}$$ 點的位置。

$$\blacksquare$$ 根據上一次計算的結果,我們將 $$1.4$$ 與 $$1.5$$ 之間等分十份,將等分點 $$1.41$$ 到 $$1.49$$ 這九個數作平方,結果如下表。
我們立刻發現 $$1.41^2 <2$$ 但是 $$1.42^2 >2$$,所以得到 $$1.41 <\sqrt{2} < 1.42$$ 的結論,省下之後的計算過程。可見 $$\sqrt{2}$$ 的百分位是1,亦即$$\sqrt{2}=1.41…$$。
如果我們再將圖放大並加上新的刻度,則也能看到下面的數線圖。
$$\blacksquare$$ 依此類推,我們再將 $$1.41$$ 與 $$1.42$$ 之間等分十份,觀察以下表格。

於是我們得知 $$1.414 < \sqrt{2} < 1.415$$,亦即 $$\sqrt{2}=1.414…$$。在數線上則會呈現如下圖的狀況。
因為 $$\sqrt{2}$$ 如我們所知是無理數,所以像這樣的步驟可以不斷地繼續下去,不斷地讓 $$\sqrt{2}$$ 落在下一個十等分段落中的其中一段,並逼近更確切的數字,就像拿一個放大鏡不斷放大、換成顯微鏡繼續放大、再換成數位顯微鏡持續放大一般,這樣的流程可以永無止盡地持續下去。然而已知 $$\sqrt{2}$$ 是不循環的無窮小數,我們的篇幅有限,所以停止在此。
向前連結:有理數、二的平方根、畢氏定理
向後連結:實數運算性質


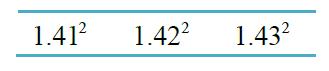



 前一篇文章
前一篇文章 下一篇文章
下一篇文章

{b} in {1,2,3,4,5,6,7,8,9,10}
應該改成 {b} in {0,1,2,3,4,5,6,7,8,9,}
同樣地,{b_k} in {1,2,3,4,5,6,7,8,9,10}
也應該改成{b_k} in {0,1,2,3,4,5,6,7,8,9}
另外有一段也需要堪誤!
「我們立刻發現1.4^22,所以得到1.41<√2<1.42的結論,省下之後的計算過程。可見√2的百分位是1,亦即√2=1.41…。」
其中,一開始的1.4^2<2,應該改成1.41^2<2
之前的堪誤還是沒有更新……很久了……
eggsu 您好
勘誤已修正,非常謝謝您。
(2011年的留言尚待確認。)
管理員 敬上