點估計及區間估計

點估計及區間估計 (Point Estimation and Interval Estimation)
國立臺灣大學農藝所生物統計組碩士班 賴薇云

一、前言

統計學可分為主要的兩個分支，敘述統計及推論統計。在我們對感興趣的母群體進行抽樣後，所得到的樣本資料凌亂不堪，無法提供任何訊息。此時，我們可以將原始資料整理成圖表或敘述統計量（平均值、變異數等），讓我們對資料的輪廓有一定的基本認識，例如資料分布的中心點、變異性、對稱性及偏歪性等，這就是敘述統計學。推論統計學則是由樣本資料的特徵，反推母群體的特徵。推論統計學又可分為估計和檢定，其中，我們從母群體抽出樣本後，計算樣本統計量來推論母體參數的過程就稱為估計。估計又可細分為點估計及區間估計，將於本篇進行介紹。

二、點估計

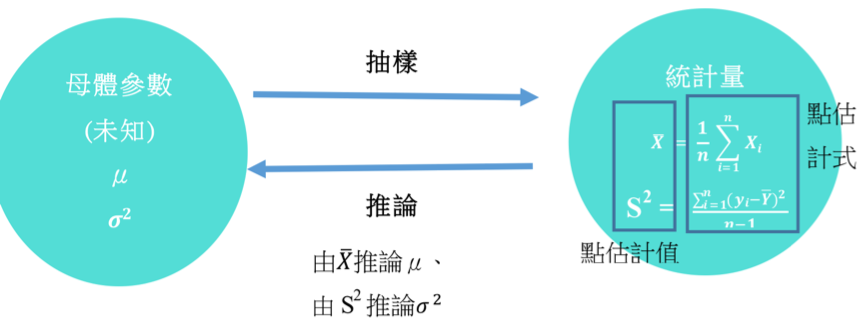
舉例來說，我們藉由樣本平均值 \(\overline{X}=\frac{1}{n}\sum^n_{i=1}X_i\) 來估計母群體參數 \(\mu\)，樣本統計量為一單一的值，所以該估計方式是以「點」猜測「點」，因此又稱為點估計（見圖一）。可用於估計相同母群體參數的點估計式可能不只一個，例如母群體參數 \(\mu\) 除了用平均值估計外，也可以用中位數來估計。我們可以藉由評估估值的無偏性、有效性及一致性，來判斷估值的好壞，進而找到最佳的估值（參考《無偏性與有效性》一文）。

圖一、點估計的流程。（本文作者賴薇云繪）

三、區間估計

區間估計是對欲估計母體參數值提供可能發生的範圍（區間），並提供該區間會包含母體參數的機率值（信賴程度），因此，母體參數值的區間估計又常稱為母體參數值的信賴區間 (confidence interval)。以下以建立一個母體參數 \(\mu\) 的 \(100(1-\alpha)\%\) 信賴區間為例，介紹如何建立信賴區間。

若樣本來自常態分布，且此常態分布的變方已知為 \(\sigma^2\)，欲估計未知的母體平均值 \(\mu\)，因此由此母體抽取大小為 \(n\) 的樣本，計算樣本均值為樣本平均值的抽樣分布 \(\overline{X}\sim N(\mu,\frac{\sigma^2}{n})\)，若是族群非常態分布，在 \(n\) 夠大的情況下，可利用中央極限定理將樣本視為近似常態分布。

再將 \(\overline{X}\) 進行標準化得  \(Z=\displaystyle\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)\)，

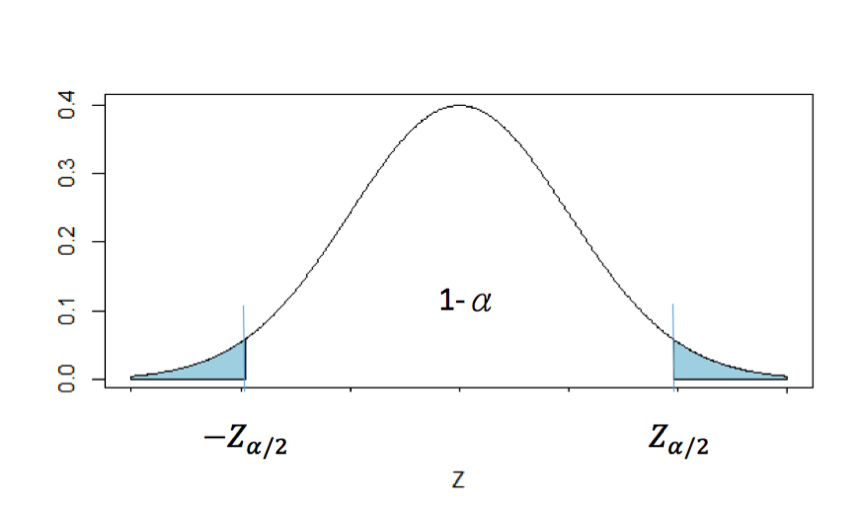
\(P\left(-Z_{\alpha/2}\le Z\le Z_{\alpha/2}\right)=1-\alpha,~~~0\le \alpha \le 1\)（如圖二）

圖二、信賴區間示意圖。（本文作者賴薇云繪）

我們要求的是 \(\mu\) 的 \(100 (1-\alpha)\%\) 信賴區間，因此進行移項：

\(\displaystyle P\left(-Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \le \overline{X}-\mu \le Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \right)=1-\alpha\)

\(\displaystyle P\left(-\overline{X}-Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \le -\mu \le -\overline{X}+Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \right)=1-\alpha\)

\(\displaystyle P\left(\overline{X}+Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \ge \mu \ge \overline{X}-Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \right)=1-\alpha\)

\(\displaystyle P\left(\overline{X}-Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \le \mu \le \overline{X}+Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}) \right)=1-\alpha\)

意即，區間 \(\left[\overline{X}-Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}}),\overline{X}+Z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}})\right]\) 涵蓋 \(\mu\) 的機率為 \(1-\alpha\)，此為 \(\mu\) 的 \(100 (1-\alpha)\%\) 信賴區間，亦可表示成 \(\overline{X}\pm Z_{\frac{\alpha}{2}}\times\frac{\sigma}{\sqrt{n}}\)，而 \(1-\alpha\) 稱為信賴係數。

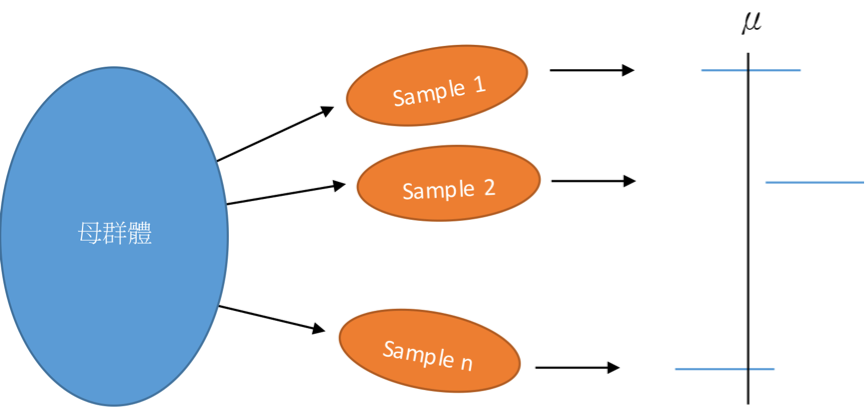
我們有 \(100 (1-\alpha)\%\)  的信心說明該區間涵蓋 \(\mu\)，若是今天從母群體抽樣 \(n\) 的個體，並建立信賴區間，重複進行 \(100\) 次之後，至少有 \(100 (1-\alpha)\) 個信賴區間涵蓋母體參數（如圖三）。

圖三、信賴區間涵蓋率示意圖。（本文作者賴薇云繪）

一般而言，我們都希望區間涵蓋母體參數的機率越高越好，當 \(\alpha\) 值越小時，該區間包含母體參數的機率越高，但信賴區間的寬度也會增加（如表一），因此實務上經常使用 \(\alpha=0.05\) 求得之 \(95\%\) 信賴區間。而在 \(\alpha\) 值固定為 \(0.05\) 的情況下，我們可以藉由增加樣本數的大小，來降低信賴區間的寬度（如表二）。

表一、標準常態分布在樣本數為 \(20\) 時不同 \(\alpha\) 值下的信賴區間

表二、標準常態分布在 \(\alpha = 0.05\) 時不同樣本數下的信賴區間

信賴區間相較於點估計值可以提供更多的資訊給決策者做決定，假設今天有一肥料即將上市，進行肥料處理後和未進行肥料處理的產量差異為 10 kg，但計算 \(95\%\) 信賴區間後，產量差異的信賴區間為 1~19 kg，或是 9~11 kg，雖然兩者的點估計值是相同的，但變異程度卻相差很多。有了區間估計，決策者可以藉由變異程度來決定要不要使用這個肥料。

參考文獻

1. 沈明來 (2014)。生物統計學入門。九州。
2. 郭寶錚、陳玉敏 (2011)。生物統計學。五南。
3. Hogg, R. V., Tanis, E., & Zimmerman, D. (2015). Probability and statistical inference (9^th edition). Pearson Higher Ed.