輾轉相除法(III) (Euclidean algorithm)

輾轉相除法(III) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師

連結：輾轉相除法(II)

一、輾轉相除法與連分數

首先讓我們來練習一下輾轉相除法，求 $$(42897, 18644)=\underline{~~~~~~~~~~~~~~~}$$。
（1）橫式過程：

$$42897=2\times 18644+5609$$
$$18644=3\times 5609+1817$$
$$5609=3\times 1817+158$$
$$1817=11\times 158+79$$
$$158=2\times 79+0$$

$$\therefore \left( {42897,18644} \right) = \left( {18644,5609} \right) = \left( {5609,1817} \right) = \left( {1817,158} \right) = \left( {158,79} \right) = \left( {79,0} \right) = 79$$

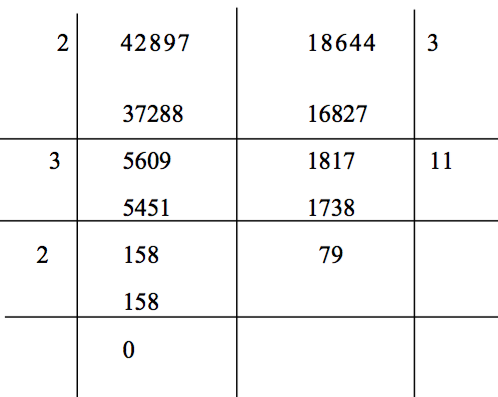
（2）直式過程：

接下來求 $$\displaystyle\frac{{42897}}{{18644}}$$ 的連分數：

$$\displaystyle\frac{{42897}}{{18644}} = 2 + \frac{{5609}}{{18644}} = 2 + \frac{1}{{\displaystyle\frac{{18644}}{{5609}}}} = 2 + \frac{1}{{3 +\displaystyle\frac{{1817}}{{5609}}}} = 2 + \frac{1}{{3 + \frac{1}{{\displaystyle\frac{{5609}}{{1817}}}}}}$$

$$=\displaystyle 2 + \frac{1}{\displaystyle{3 + \frac{1}{\displaystyle{3 + \frac{1}{\displaystyle{11 + \frac{{79}}{{158}}}}}}}} = 2 + \frac{1}{{3 +\displaystyle \frac{1}{{3 +\displaystyle\frac{1}{{11 +\displaystyle\frac{1}{2}}}}}}}$$

這樣的繁分數稱為連分數。為了減少篇幅，我們可以寫成下式：

$$\displaystyle\frac{{42897}}{{18644}} = 2 + \frac{1}{3} \oplus \frac{1}{3} \oplus \frac{1}{{11}} \oplus \frac{1}{2}$$^[註1] 或 $$[2;3,1,1,2]$$

其中，$$2$$、$$2+\frac{1}{3}=2.333…$$、$$2 + \frac{1}{3} \oplus \frac{1}{3} = 2.3$$、$$2 + \frac{1}{3} \oplus \frac{1}{3} \oplus \frac{1}{{11}} = 2.30088496…$$，這些分數稱為 $$\displaystyle\frac{{42897}}{{18644}} = 2.30084746…$$ 的漸近分數。

例題1：求 $$(117, 51)=\underline{~~~~~~~~~~~~~~~}$$。

參考解法：

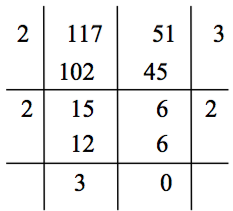
$$\because 117=51\times 2+15$$                         亦可用右式方法

$$51=15\times 3+6$$

$$\therefore 15=6\times 2+3$$

因此 $$(117,51)=(51,15)=(15,6)=3$$

例題2：將 $$\displaystyle\frac{117}{51}$$表成連分數$$=\underline{~~~~~~~~~~~~~~~}$$。

參考解法：

$$\begin{array}{ll}\displaystyle\frac{{117}}{{51}} &=\displaystyle 2 + \frac{{15}}{{51}} = 2 + \frac{1}{{\displaystyle\frac{{51}}{{15}}}} = 2 + \frac{1}{\displaystyle{3 +\displaystyle\frac{6}{{15}}}} = 2 + \frac{1}{{\displaystyle 3 + \frac{1}{{\displaystyle\frac{{15}}{6}}}}} \\&=\displaystyle 2 + \frac{1}{{3 +\displaystyle\frac{1}{{2 +\displaystyle\frac{3}{6}}}}} = 2 + \frac{1}{{3 +\displaystyle\frac{1}{{2 +\displaystyle\frac{1}{2}}}}}\end{array}$$

因此，$$\displaystyle\frac{117}{51}$$ 的連分數可以簡記為 $$[2;3,2,2]$$。

數學思維：輾轉相除法的運算過程可連結到連分數是十分有趣的，很值得讀者深究。

二、輾轉相除法與電阻問題

電阻問題歷來是最引人入勝的問題，我們回想在中學所學的電阻串聯與並聯的知識與歐姆定律，殊不知其中蘊含許多數學知識背景。現在有一個問題：如果只能用單位電阻(即電阻值為 $$1$$ 歐姆的電阻)和只能使用並聯與串聯的情況下，能否在兩點之間構成 $$q/p$$ 個單位的電阻？

我們只要將 $$p$$ 組(每組由 $$q$$ 個單位電阻串聯而成)單位電阻並聯在一起即可。

理由為假設所求的電阻為 $$R$$，$$\displaystyle\therefore\frac{1}{R} = \frac{1}{q} + \frac{1}{q} + \frac{1}{q} + …. + \frac{1}{q}$$(有 $$p$$ 個) $$=\displaystyle\frac{p}{q}$$，

$$\therefore R=\displaystyle \frac{q}{p}$$，合所求。

但是，問題是這樣的方法必須耗盡 $$p\times q$$ 個單位電阻，十分不符合經濟效益。接下來，我們要介紹一種容易了解且符合經濟效益的解法。

假設 $$p=37,~q=101$$，我們應用連分數的想法，解 $$101/37$$：

$$\displaystyle\frac{{101}}{{37}} = 2 + \frac{1}{\displaystyle{1 + \frac{1}{{\displaystyle2 + \frac{1}{{1 +\displaystyle \frac{1}{{2 +\displaystyle\frac{1}{3}}}}}}}}}$$ 即 $$[2;1,2,1,2,3]$$

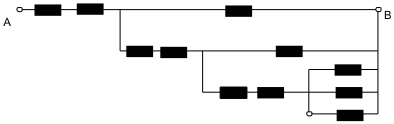
電路圖如下所示：

此時，我們只需要 $$11$$ 個單位電阻就行了，這裡補充說明一點：當 $$p,q$$ 都是質數時，只要將 $$q/p$$ 展開成連分數的形式即可。至於，當 $$p,q$$ 都是合成數時，情況就有不同，可解的方法很多，需要仔細討論才行。

[註1]：定義：$$\frac{1}{x} \oplus \frac{1}{y} = \frac{1}{{x + \frac{1}{y}}}$$

連結：輾轉相除法(IV)