貝爾太空船弔詭

貝爾太空船弔詭 （Bell’s Spaceship Paradox）
國立臺灣大學大氣科學系100級 陳品全

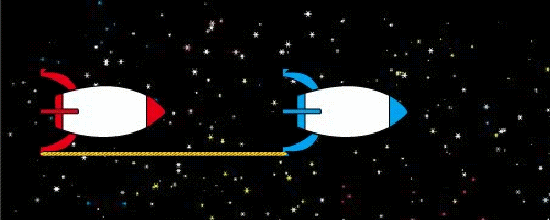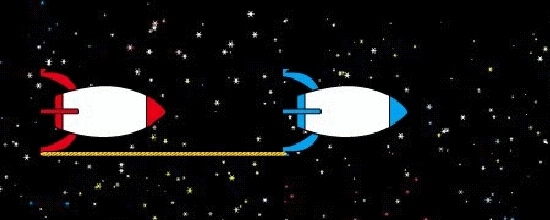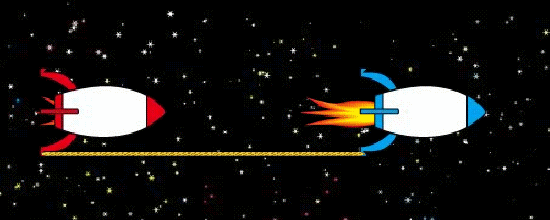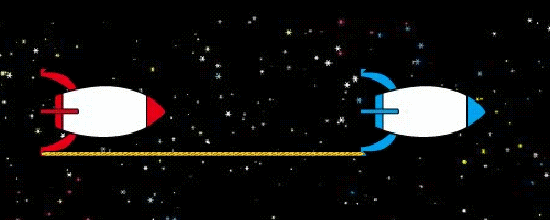
有兩艘太空船，船與船之間用一條長度為 \(L\)、剛好拉直、但又沒有張力的繩子連結著。接著，這兩艘太空船同時開始沿著 \(x\) 軸以相同的加速度對於地面上的慣性觀察者做等加速度運動（如圖1所示），所以繩子對於地面上的觀察者來說會永遠保持同樣的長度。請問，當太空船加速到很快時，繩子上面會有張力嗎？

圖1 （陳義裕繪）

直觀上我們會覺得繩長沒變，當然就沒有張力。可是根據狹義相對論，運動中的物體長度會縮短，所以要讓繩子在高速運動下相對於地面上的人還保持等長，此張力一定是大的不得了，這就是貝爾太空船弔詭。

既然根據假設，地面的觀察者發現繩長不變，那麼繩子對於太空船上的觀察者來說一定是變長了。所以矛盾的解決關鍵就在於：如何去說明繩子在兩艘太空船加速的過程中會被不斷拉長。

我們可以設立兩個觀察者，一個是“靜止”的觀察者 \(S\)（註：相對論當然沒有所謂的“靜止”，但這邊為求方便，我們用靜止坐標系形容一開始相對於兩個尚未加速的船是沒有相對速度的坐標系；也可以稱為lab observer），以及另一個跟著後方太空船一起加速的觀察者 \(S’\)。

根據勞倫茲轉換 (Lorentz transformation)，兩個觀察者所觀察到的位置與時間的關係如下
（\(S\) 觀察者觀察到 \(x,t\)；\(S’\) 觀察者觀察到 \(x’,t’\)）：

\(x’=\gamma(x-vt)~,t’=\gamma(t-vx)~,(\gamma=\frac{1}{\sqrt{1-v^2}})\)

（註：在此使用自然單位制，取真空中光速為 \(c=1\)）。
這兩個式子可以取 \(\Delta\)，也就是變化量，於是我們有了

\(\Delta x’=\gamma(\Delta x-v\Delta t)~,\Delta t’=\gamma(\Delta t-v\Delta x)\)

對於 \(S\) 來說，由於兩個艘太空船是同時在加速的，因此兩艘船之間的距離（同時也是繩子的長度）不變。但兩艘相距 \(L\) 的火箭「同時」加速時，雖然 \(\Delta t=0\)，但那麼對於 \(S’\) 來說卻不是同時的！代入公式，我們有 \(\Delta t’=\gamma(0-vL)=-vL\gamma<0\)，所以前方火箭加速的時刻其實比後方火箭來得早！既然前方火箭偷跑、加速在前，繩子會被用力拉扯、張緊就很自然了（見圖2）。

圖2 （陳義裕繪）

註：嚴格說起來，這個想像實驗不能只由一個慣性座標 \(S\) 與加速座標 \(S’\) 來描述。如果想要列出 \(\Delta x’=\gamma(\Delta x-v\Delta t)~,\Delta t’=\gamma(\Delta t-v\Delta x)\)，那麼 \(S\) 和 \(S’\) 都必須要是慣性坐標系才行。所以我們應該事先準備很多個等速度向前行進的 \(S’_i\)，而每一個 \(S’_i\) 的速度會分別等於在不同時刻 \(t_i\) 時後方太空船的前進速度。（也就是說在時刻 \(t=t_i\) 的瞬間，\(S’_i\) 與後方太空船的相對速度為 \(0\)）

參考文獻

1. 台灣大學物理系陳義裕老師狹義相對論演講資料.
2. 台灣陳義裕老師相對論上課筆記.
3. 高瞻平台. 同時的相對性.（/highscope/?p=1541）