貝氏定理(Bayes’ theorem)

貝氏定理(Bayes’ theorem)
國立屏東高級中學數學科楊瓊茹老師

明天下雨機率是多少？日常生活中我們總是會使用到機率的概念，但是在語句用詞上若不夠周延，就很容易把「在 \(A\) 事件發生的情況下，\(B\) 事件發生的機率」與「在 \(B\) 事件發生的情況下，\(A\) 事件發生的機率」混為一談，也就是把 \(P(B|A)\) 和 \(P(A|B)\) 在邏輯上的不同給忽略了。

這是一個常犯的錯誤，舉例來說：某數學家做愛滋病毒HIV篩檢，醫師告訴他：「檢驗結果是陽性，我真的很遺憾，你只有千分之一的機會能活超過十年。」當下，數學家被醫生的死刑宣判震驚的一時無法言語，但片刻回復冷靜後，他以數學邏輯思維的方式進一步地問清楚醫生所判斷的機率值，才知道為什麼醫生說他只有千分之一的機會是健康的。原來，「千分之一」的意思是「不是愛滋病帶原者，但HIV檢驗結果呈現陽性的機會，是每 \(1000\) 個血液樣本中有 \(1\) 個。」，即 \(\frac{1}{1000}\)。

醫生一開始宣判死刑的說法乍聽之下似乎是有道理的，但事實並非如此，因為他將 \(P(\)檢驗呈陽性│沒有愛滋病帶原\()\) 倒置為 \(P(\)沒有愛滋病帶原│檢驗呈陽性\()=\frac{1}{1000}\)。

那麼，在檢驗呈陽性的情況下，數學家有沒有可能是被誤檢？沒有愛滋病帶原的機會是多少？即 \(P(\)沒有愛滋病帶原│檢驗呈陽性\()\) 究竟是多少？底下，我們使用貝氏定理來分析：

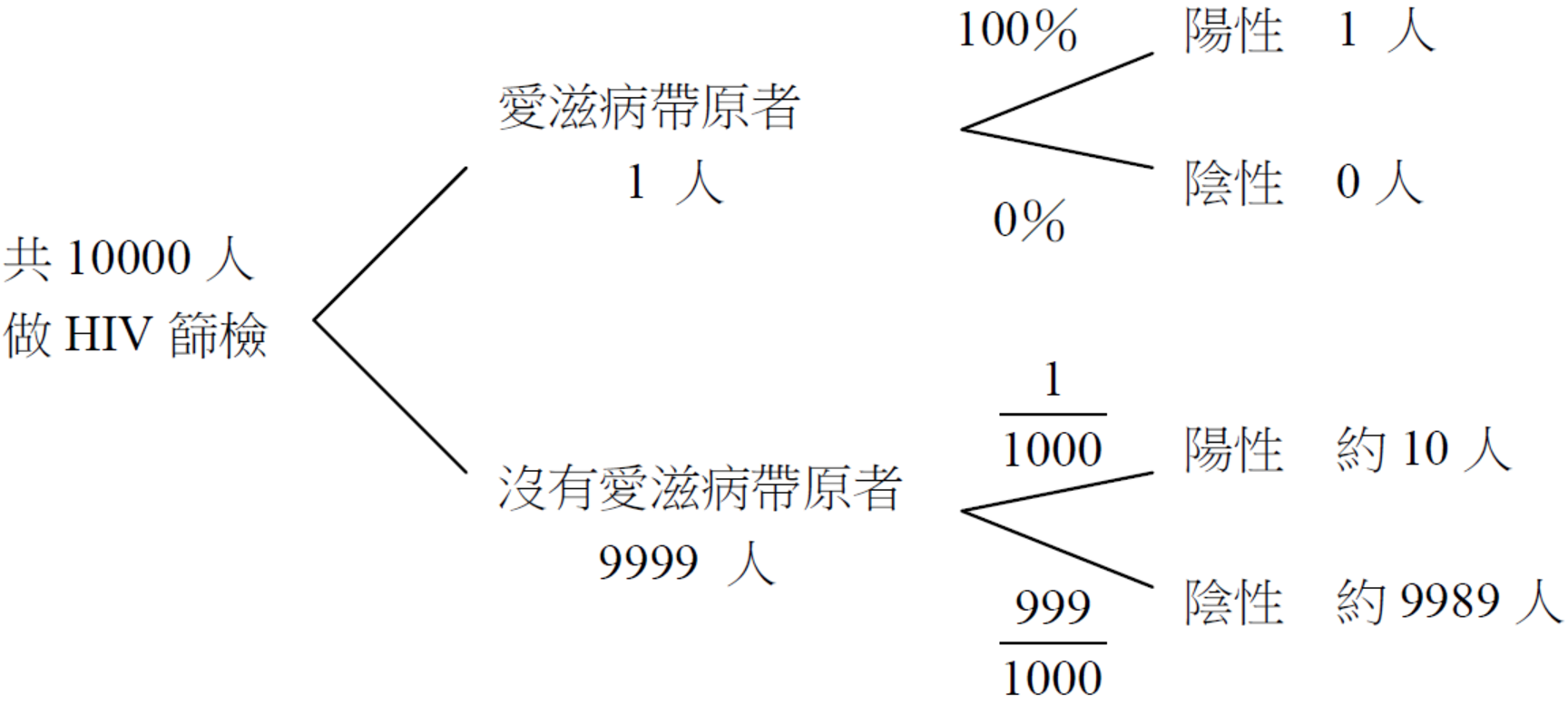
假設總共有 \(10000\) 人做愛滋病毒HIV篩檢，根據疾病管制中心的數據得知，差不多有 \(1\) 人確實感染愛滋病，患此病的人經血液篩檢 \(100\%\) 會呈現陽性；不患此病的人，有 \(\frac{1}{1000}\) 會被誤檢而呈現陽性：

所以，\(P(\)沒有愛滋病帶原│檢驗呈陽性\()\approx \frac{10}{1+10}=\frac{10}{11}\)。數學家是健康的機會大約高達十一分之十，而非千分之一。

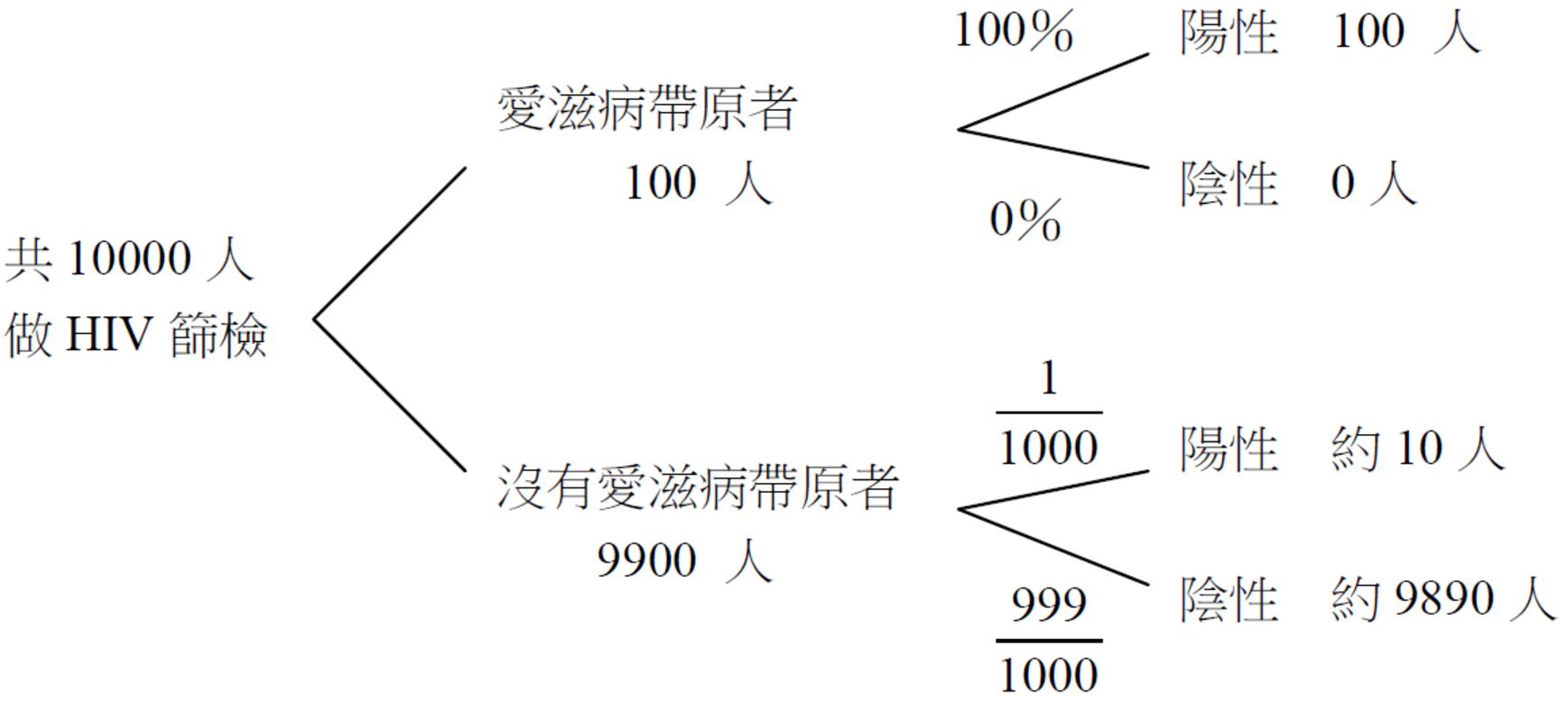
除了正確解讀陽性反應的意義，考慮疾病是否盛行或是否屬於高危險群也是檢驗的評估要項。例如上述 \(10000\) 個篩檢中，愛滋病帶原者高達 \(100\) 人，

因此，\(P(\)沒有愛滋病帶原│檢驗呈陽性\()\approx\frac{10}{100+10}=\frac{1}{11}\)。這種情形下，檢驗呈陽性，代表感染愛滋病的機會大約高達 \(\frac{10}{11}\)。

在上述的愛滋病篩檢例子中，醫生用一個機率值來傳達特定的資訊。我們在生活中或資訊媒體中，也隨時可見許多數據，如何正確解讀正是不可或缺的數學素養。底下，我們來欣賞貝氏定理：

設 \(\{A_1,A_2,\cdots,A_n\}\) 為樣本空間 \(S\) 的一組分割，\(B\) 為 \(S\) 的任一個事件。

若 \( P(B)>0\)，\(P(A_i)>0,~~(i=1,2,\cdots,n)\)，

則在事件 \(B\) 發生的情況下，事件 \(A_k\) 發生的機率為

\(\displaystyle P(A_k|B)=\frac{P(A_k)P(B|A_k)}{\sum\limits^n_{i=1}P(A_i)P(B|A_i)}\)，\(k=1,2,\cdots,n\)

貝氏定理出現在十八世紀英國長老派教會牧師貝氏( Reverend T. Bayes, 1702-1761)所寫的一篇論文中，論文題目是〈關於解決機遇論的一個問題〉，貝氏將此篇文章留給也是牧師的數學家普萊斯 (Richard Price)，1764年被發表於英國皇家學會的會刊上。

今日，它被廣泛應用在許多領域中，例如：犯罪審判、品管檢驗、保險理賠等。假定我們碰到的現象背後原因有很多個時，貝式定理可以幫助我們經由分析各項原因的事前機率和蒐集的新資訊，反推測哪個才是主要的原因，進而幫助我們做出正確的判斷和決策。

參考資料：

1. 曼羅迪諾著、胡守仁譯(2012)，《醉漢走路-機率如何左右你我的命運和機會》，台北：天下遠見出版社。
2. 小島寬之著、鄭宇淳譯(2007)，《從數學看人類的進步軌跡》，新北市：世茂出版。