矩陣(Matrix)
矩陣(Matrix)
國立臺南第一高級中學數學科林倉億老師
摘要:本文介紹何謂矩陣及矩陣的相等。
我們經常將許多資料以表格的方式呈現,不僅易於掌握資料,也利於後續的分析。如右表是某家工廠每一季銷售甲、乙、丙三型產品的數量,從表格中我們不僅可以知道每一季的銷售總量,更可以很快地掌握到甲型產品不會受到季節性因素的影響,銷售量大抵上都是10個左右;至於乙、丙型的產品,顯然就與季節性因素有很大的關聯,一個是逐季遞增,另一個恰好相反,是逐季遞減。如果這種銷售趨勢在不同的年度不會有太大的改變,那工廠負責人就可以據此來準備生產所需的零件,甚至是工廠工人的工作時數等等。
倘若我們今天只將上述表格中的數字依相對位置寫下來,然後在前後加上括號,如:$$\left[ \begin{array}{l} \begin{array}{*{20}{c}} {10}&{12}&{13}&{12} \end{array}\\ \begin{array}{*{20}{c}} {50}&{40}&{30}&{20} \end{array}\\ \begin{array}{*{20}{c}} {20}&{30}&{40}&{50} \end{array} \end{array} \right]$$ 或 $$\left( \begin{array}{l} \begin{array}{*{20}{c}} {10}&{12}&{13}&{12} \end{array}\\ \begin{array}{*{20}{c}} {50}&{40}&{30}&{20} \end{array}\\ \begin{array}{*{20}{c}} {20}&{30}&{40}&{50} \end{array} \end{array} \right)$$,看起來就像數字排成矩形的陣式,我們就稱呼它為「矩陣」(matrix)。矩陣在數學、工程、商業等等領域中佔有非常重要的地位,關於矩陣的學問就稱為「線性代數」(Linear Algebra)。有數學家預言,線性代數將取代微積分成為未來大學數學的必修科目。讓我們先認識矩陣的基本組成。
在矩陣中,我們將橫寫的稱為「列」(row),直寫的稱為「行」(column),矩陣中的元素(上述例子中的元素就是數字)簡稱為「元」(entry)。例如在上述的矩陣中,第 $$1$$ 列就是 $$\left[ {\begin{array}{{c}} {10}&{12}&{13}&{12} \end{array}} \right]$$,只有 $$1$$ 列的矩陣,我們稱為「列矩陣」;第 $$2$$ 行就是 $$\left[ {\begin{array}{{c}} {12}\\ {40}\\ {30} \end{array}} \right]$$,只有 $$1$$ 行的矩陣,我們稱為「行矩陣」。第 $$1$$ 列第 $$2$$ 行的元就是 $$12$$,第 $$2$$ 列第 $$1$$ 行的元就是 $$50$$,以此類推…。上述的矩陣共有 $$4$$ 列 $$3$$ 行,所以我們稱它為 $$4\times 3$$ 階矩陣。
一般而言,若一個矩陣 $$A$$ 有 $$m$$ 列 $$n$$ 行時,我們就稱為「$$m\times n$$ 階矩陣」,
表示成 $$A = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots &{\ddots}& \vdots \\ {{a_{m1}}}&{{a_{m2}}}& \cdots &{{a_{mn}}} \end{array}} \right]$$,可簡記作 $${A_{m \times n}} = \left[ {{a_{ij}}} \right]$$,或 $$A = {\left[ {{a_{ij}}} \right]_{m \times n}}$$,
其中 $$a_{ij}$$ 就代表矩陣 $$A$$ 中第 $$i$$ 列第 $$j$$ 行之元。
而當矩陣的列數與行數相等時,即 $$m=n$$ 時,我們就稱之為「方陣」,或是「$$m$$ 階方陣」。
當我們說 $${A_{m \times n}} = \left[ {{a_{i j}}} \right]$$ 與 $${B_{p \times q}} = \left[ {{b_{i j}}} \right]$$ 相等時,就是說這兩個矩陣其實就是同一個,也就是說,不論是列數、行數,還是相同位置的元,統統要一樣,用符號來表示就是 $$m=p$$、$$n=q$$ 且 $$a_{ij}=b_{ij}$$(對同一組 $$i$$、$$j$$)。
最後要提醒讀者,在初接觸矩陣時,我們習慣將每個元 $$a_{ij}$$ 都看作是數字,但這並不是一成不變的,$$a_{ij}$$ 也可能是函數,甚至是矩陣!由於這會牽涉到比較高深的線性代數,在此我們並不打算繼續深究下去。往後,若沒有特別提及,我們仍是將矩陣的元當作是一般的數字。


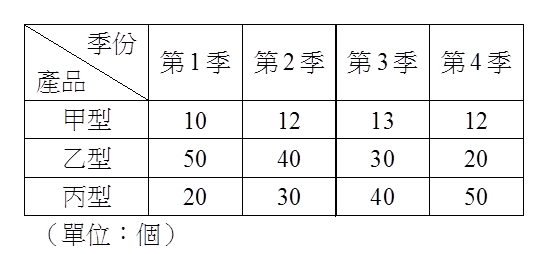
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
