畢氏定理(Pythagoras Theorem)

畢氏定理(Pythagoras Theorem)
國立蘭陽女中數學科陳敏晧老師

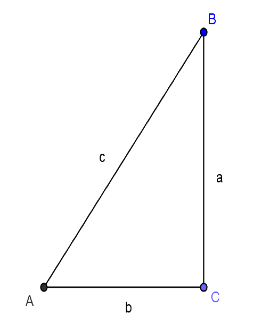已知：直角三角形 $$ABC$$，其中 $$\angle BAC=90^\circ$$，

而 $$\overline{AB}=c$$，$$\overline{BC}=a$$，$$\overline{CA}=b$$。

求證 $$a^2+b^2=c^2$$。

證明：

方法一：《幾何原本》作法

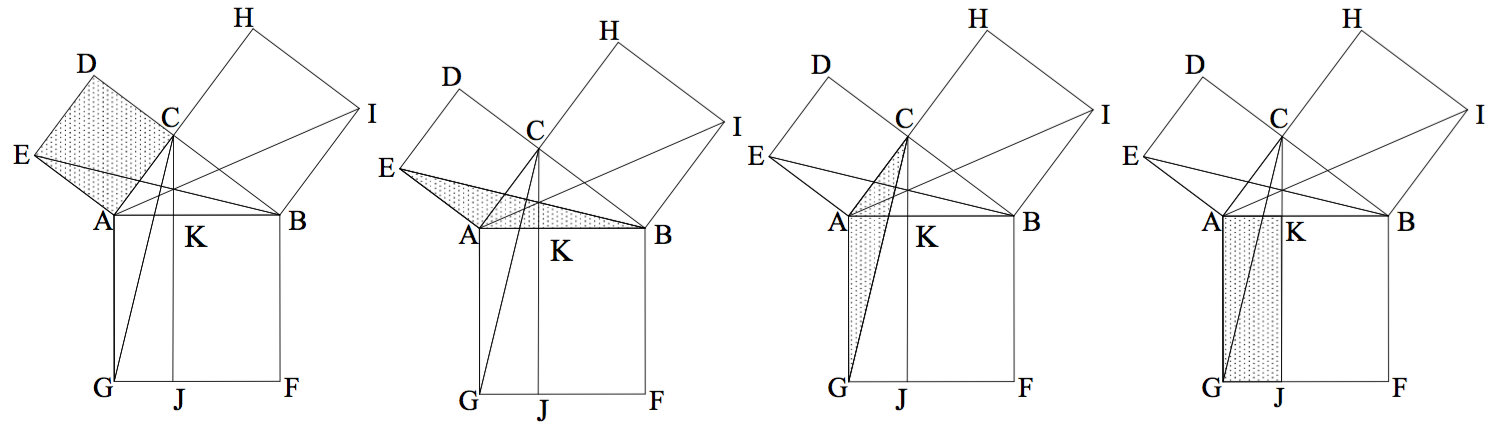
由直角 $$C$$ 往斜邊 $$\overline{AB}$$ 作直線，交 $$\overline{AB}$$ 邊於 $$K$$ 點，交 $$\overline{GF}$$ 邊於 $$J$$ 點。只要證明正方形 $$ACDE$$ 的面積等於長方形 $$AKJG$$ 的面積；正方形 $$BCHI$$ 的面積等於長方形 $$BKJF$$ 的面積，便完成畢氏定理的證明。

以正方形 $$ACDE$$ 的面積等於長方形 $$AKJG$$ 的面積為例，歐幾里得利用：

$$(1)$$正方形 $$ACDE$$ 的面積等於 $$2$$ 倍三角形 $$AEB$$ 的面積(同底等高)；
$$(2)$$三角形 $$AEB$$ 與三角形 $$ACG$$ 全等($$SAS$$全等)。
$$(3)$$ $$2$$ 倍三角形 $$ACG$$ 的面積等於長方形 $$AKJG$$ 的面積(同底等高)

同樣的道理，也能證明正方形 $$BCHI$$ 的面積等於長方形 $$BKJF$$ 的面積，即 $$\overline{AC}^2+\overline{BC}^2=\overline{AB}^2$$

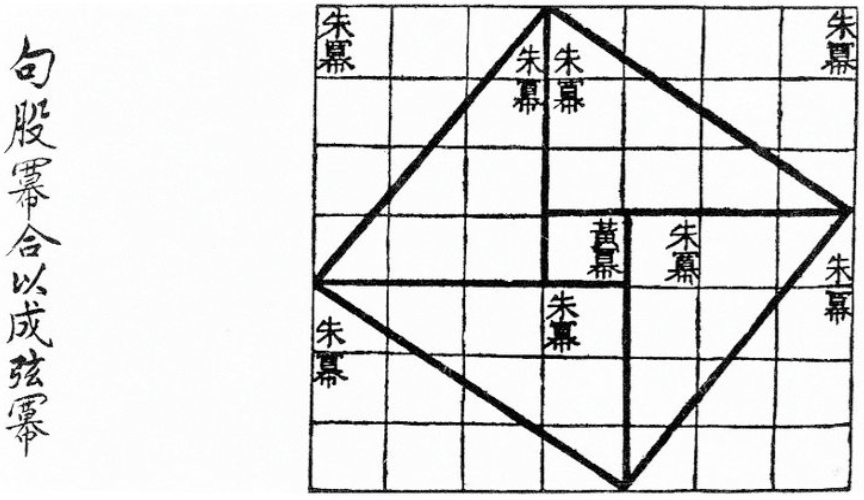
 方法二：《周髀算經》作法

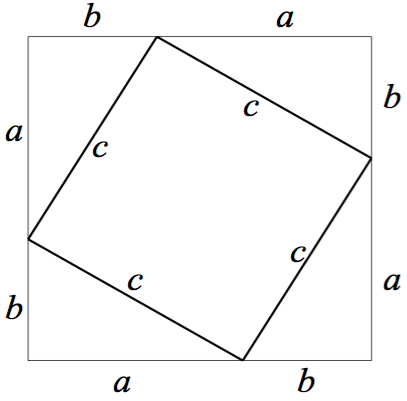大的正方形(邊長為 $$a+b$$)面積等於 $$4$$ 個直角三角形和一個小的正方形(邊長為 $$c$$)面積的和。

因此，$$(a+b)^2=4(\frac{1}{2}ab)+c^2$$

$$\therefore a^2+2ab+b^2=2ab+c^2$$，即 $$a^2+b^2=c^2$$

《周髀算經》卷上：「故折矩以為勾廣三、股修四、徑隅五。」即是最簡單的勾股數：$$3,~4,~5$$。

《九章算術》勾股章第14題(譯成今文)：

假設甲、乙二人站在同一地點出發，若甲的速率：乙的速率$$=7:3$$，現在乙向東走，而甲先向南走 $$10$$ 步，再斜向東北走，最後與乙相遇，請問：相遇前甲斜向走幾步？乙向東走幾步？

參考答案：甲斜向走 $$14\frac{1}{2}$$ 步、乙向東走 $$10\frac{1}{2}$$ 步。

數學思考：已知 $$ABCD$$ 為矩形，$$P$$ 為內部一點，若 $$\overline{PA}=3,~\overline{PB}=4,~\overline{PC}=2$$，求 $$\overline{PD}=\underline{~~~~~~~~~}$$。

參考答案：$$\overline{PD}=\sqrt{21}$$

拉婓爾(Raffaello Sanzio, 1483-1520)所畫《雅典學院》中的畢達哥拉斯(郵票左下方正在讀書的禿頭男子)。右下圖為畢氏定理的紀念郵票。

附註1：路明思(Elisha Scott Loomis, 1852-1940)所著的《畢氏定理(The Pythagorean Proposition)》一書，收集了367個畢氏定理的各式證法。

附註2：根據直角三角形中的畢氏定理，可以導出三角函數的平方關係 $${\sin ^2}\theta+ {\cos ^2}\theta= 1$$;$$1+ {\tan ^2}\theta= {\sec^2}\theta$$;$$1 + {\cot^2}\theta= {\csc^2}\theta$$