準確度和精確度
準確度和精確度 (Accuracy and Precision)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯
科學是一種歸納的學問,實驗則是檢驗真理的唯一準則,因此,實驗數據的可信度一直都是最核心的問題。如何判斷實驗數據可不可信,科學家以準確度(Accuracy)與精確度(Precision)為重要的參考指標。
準確度(Accuracy)是一個統計學上的概念,指在每一次獨立的測量之間,其平均值與已知的數據真值之間的差距。若多次測量其平均值接近於已知的數據真值(理論值或期望值),我們可以相信數據「準確」,或是數據具有「高準確度」。反之,若多次測量其平均值與已知的數據真值差距較大,表示實驗數據不準確,或準確度不高。準確度廣泛應用於各類學科,尤其是分析化學。
一般而言準確度可以利用絕對誤差(absolute error)、相對誤差(relative error)等兩種方式表示,其數學定義如下:
絕對誤差:\(E=\bar{x}-x_t\)
相對誤差:\(\displaystyle E_r=\frac{\bar{x}-x_t}{x_t}\times 100\%\)
其中 \(\bar{x}\) 為已知的數據真值,或數據平均,\(x_t\) 為任一實驗值。絕對誤差具有單位,而相對誤差則無,是利用百分比(%)的方式表示。分析化學上常以相對誤差表示,易於瞭解實驗值與數據真值(理論值)的誤差大小。而一個實驗方法準確與否,很大成分取決於進行分析時的誤差要求,一個需要精密測量的實驗的誤差容忍範圍,比粗估的分析分析法要小很多,因此,選擇一個準確度高的分析方法,是分析化學當中非常重要的一環。
當要求實驗數據很精準時,我們同時會要求實驗有高度的「再現性」,表示我們取得的實驗數據是可信的,也就是實驗數據需要具有高「精確度(precision) 」。精確度同樣是一個統計學上的概念,指各次獨立實驗數據之分佈的「集中程度」。通常多次測量值的彼此之間的差距小,顯示精確度高;反之若多次測量值彼此之間的差距較大,則此系列實驗不夠精確,即精確度低。
在實驗數據呈現常態分佈的情況之下,精確度可以利用測量值的樣品標準差(standard variation)、變異(variance)、變異係數(variance of coefficient)來度量。常用的精確度參數指標,標準差 \(\sigma\),其定義如下:
標準差 \(\displaystyle \sigma=\sqrt{\frac{\sum^n_{i=1}(x_i-\mu)^2}{n-1}}\)
其中 \(x_i\) 為第 \(i\) 次的測量值,\(n\) 為測量次數,\(\mu\) 為平均值。
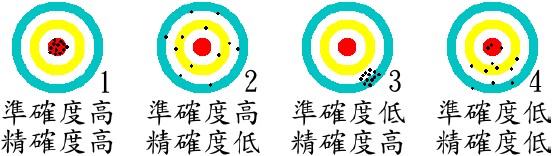
準確度與精確度以不同的面向來描述數據的不確定性或者可確定的程度,雖然兩者的定義明顯不同,但大多數人常把他們搞混了。為了清楚得說明兩者,我們以「打靶」為例:
如圖1,當子彈(即實驗數據)時全數命中紅心(極接近理論值),顯示精確度高、準確度高。但如下圖3所示,即使彈孔集中於某一區域,具有高精確度,由於此集中區域偏離靶心,所以準確度低,這是在測量時比較常見的結果。至於圖2,彈孔均勻分布於靶紙上,表示精確度很低時,雖然所有測量值的平均值相當接近於真值,卻不是真的「準確」。
理想的測量經常是被認為準確且精確的。然而由於測量時的系統誤差(systematic error)以及隨機誤差(random error),會造成準確度與精確度的降低。其中系統誤差會造成準確度的降低;要了解系統誤差所造成的影響,則可以搭配其他的分析方式,或者是進行空白實驗、改變樣品濃度等等。相對於準確度大多由系統誤差造成,精確度大多是由隨機誤差所造成。精確度經常被用來表達儀器的再現性,即利用完全相同的實驗方法,所得到的數據其接近程度;通常一個分析儀器的精確度可以透過重複測量的方式獲得。一個分析儀器的精確度高,代表著一個分析儀器對於不同樣品濃度的分析樣品具有良好的鑑別度,為儀器分析方法良莠的重要指標之一。而儀器分析的品質提高,代表了對於相近的訊號,能夠有著較好的分辨能力。
在定量分析當中,經常以所有測量值的平均值為測量之準確值,如此一來便無法計算準確度,造成系統誤差被忽略,因此需要建立一個反覆測量且具良好再現性參考標準。現今常用的標準值由美國國家標準與技術研究所(NIST, National Institute of Standard and Technology)等機構所建立。
備註:關於準確度與精確度的定義的討論,還可參考 史天元著,地籍測量 第 32 卷第 3 期,第 18-26 頁「準確度與精密度」。(感謝讀者學圃提供資訊)
資料來源
1. Zumdahl, S. S. Chemical Principles, 5th edition; Houghton Mifflin Company: Boston, 2003; p. A69.
2. Harris, D. C. Quantitative Chemical Analysis, 7th edition; W. H. Freeman and Company: New York, 2007; pp. 43-44.
3. Wikipedia—accuracy and precision http://en.wikipedia.org/wiki/Accuracy_and_precision


 前一篇文章
前一篇文章 下一篇文章
下一篇文章

圖片是不是打錯了?!
您好,經本文責任編輯確認,圖片是沒有錯的喔!
管理員teresa敬上
大學普化和分析在教的時候,我們老師都把precision翻成”精密度”,這好像更符合他的定義喔,可以參考看看。
hazelnut您好
關於英文譯名部分,本網站採用國家教育研究院審譯的「雙語「雙語詞匯、學術名詞暨辭書資訊網」之譯名。
不過不同學科譯名也會有所不同,所以「精確度」或「精密度」都是正確的。
謝謝您的關注!
管理員teresa敬上
圖片錯囉
圖片中2和4號的說明應該對調才對
Kevin您好
經本文責任編輯確認,圖片並無誤,解釋如下:
「圖2,子彈打在靶上,雖然分散但均勻分佈在靶心周圍,準確度高;但彈孔分散在靶上,不能集中於靶某個位置,顯示精確度不佳。
圖4,子彈打在靶上,平均位置雖於靶某個位置但偏離靶心,準確度低,又彈孔不集中於很小範圍內,顯示精確度低。」
管理員teresa 敬上
謝謝回復,建議可以參考SKOOG等人所著的Fundamentals of Analytical Chemistry一書的第八版第93頁
的圖片,較不會讓讀者產生誤解
常見文獻以射擊彈著點分佈情形來說明準確度與精密度的意義如圖示,初看似乎簡明易懂,實際仍隱含認知的盲點;以射擊而言每一彈著點均儘量接近靶心才稱得上精確或是精準,圖2所示彈著點分佈其平均值雖接近靶心,不少文獻依準確度的定義謂其屬於高準確度低精密度,明顯與一般對射擊是否精準的常識認知相違,其實仍屬於低準確度低精密度。
“至於圖2,彈孔均勻分布於靶紙上,表示精確度很低時,雖然所有測量值的平均值相當接近於真值,卻不是真的「準確」。”
既然如此,圖下方之說明就不宜為準確度高,精確度低,以免讀者誤解。
學圃您好:
謝謝您對於本文的來信,基於尊重作者與開放大家對文章內容的討論,我們不直接大幅修改文章內容,您對本文建議與質疑之處,我們在此張貼您對本文後半修正部份:
準確度與精密度以不同的面向來描述數據的不確定性或者可確定的程度,雖然兩者的定義明顯不同,但一般人還是常把他們搞混了。常見文獻以射擊彈著點分佈情形來說明準確度與精密度的意義,初看似乎簡明易懂,如果沒有仔細說分明,實際仍然容易導致錯誤的認知。
以射擊而言,每一彈著點均儘量接近靶心如圖1所示,才稱得上俗語說的「精準」。圖2表示彈著點分佈其平均值接近靶心,不少文獻依準確度的定義就直接解釋其屬於準確度高、精密度低,這高準確度明顯與一般對射擊是否「精準」的常識認知相違,其間到底出了什麼差錯?
我們也嘗試以「打靶」為例,希望能夠依學理清楚說明兩者的意義,而且與與一般對射擊結果是否「精準」的常識認知不致相違:
正式使用槍枝以前我們必須確認其瞄準機制與正常情況下的彈道一致,比較有效的方法當然是由射擊好手來「試槍」,其結果可能如圖2,其彈著分佈偏離靶心的狀況可做為調校槍枝瞄準機制的依據。
同一槍枝經過調校,再由射擊好手瞄準靶心,其結果應當如圖1,子彈(或實驗數據)幾乎全數命中紅心(或極接近理論值),顯示精密度高、準確度亦高。
經過調校的槍枝,如果由技術平平者再次「試槍」,其彈著分佈應該類似圖2,即彈孔分佈之平均位置接近靶心,以試槍為目的而言,仍屬準確度高,惟彈著分散,屬於精密度低的「試槍」結果,意謂若由其多次重復「試槍」,結果相近,或者「再現」的機率較低。
「試槍」這樣的操作,與測量的測定、測設放樣的性質最為類似,即未知其真值或真實位置,「試槍」時靶心的角色只是提供試槍的參考位置。同樣是如圖2的彈著分佈,如果是以爭取高分為目的的射擊競賽結果,則如一般常識認知,屬於準確度低、精密度亦低,不夠「精準」的射擊結果。
技術平平的射擊手取得槍枝隨即瞄準射擊,很可能得到如圖4準確度低、精密度亦低的的彈著分佈,當然就更不「精準」了。
準確且精密的結果是理想的測量或科學實驗追求的目標。然而由於測量時的系統誤差(systematic error)以及隨機誤差(random error);即使相當精密,「再現性」很高的實驗,因為稍大的系統誤差導致準確度降低,整體成果的「精準」程度也隨之降低了。以分析化學為例,要瞭解系統誤差所造成的影響,可以搭配其他的分析方式,或者是進行空白實驗、改變樣品濃度等等。
相對於系統誤差影響準確度,隨機誤差影響精密度。精密度經常用來表達儀器的再現性,即以完全相同的實驗方法,所得到的數據其接近程度;通常一個分析儀器的精密度可以透過重複測量的方式得知。例如分析濃度儀器的精密度高,代表分析儀器對於不同濃度的待分析樣品具有良好的鑑別度,為儀器分析方法良莠的重要指標之一。而儀器分析的品質提高,代表了對於相近的訊息,能夠有著較好的分辨能力。
在化學定量分析當中,經常以所有測量值的平均值為測量之準確值,由於系統誤差被忽略,無法得知分析結果的準確度,因此需要建立一個反覆測量且具良好再現性的參考標準。現今國內常用的標準值由美國國家標準與技術研究所(NIST, National Institute of Standard and Technology)等機構所建立, NIST為產業界、學術界、政府及其他用戶提供了一千三百餘種標準參考材料(SRMs)。這些物品特定的量度或成分含量經認證後成為校正標準,用於測量設備和製作程式、工業生產的品質控制標準,以及實驗對比樣本。
日益受到重視的國際標準組織ISO發表一份標準文件ISO5725,其名稱為”Accuracy (trueness and precision) of measurement methods and results”(量測方法與成果之準確度(真實度與精密度)),其內涵最大的改變是趨向從俗的定義Accuracy為一般用語(the general term),即我們前文用來描述量測、實驗整體成果的「精準」度一詞,或者簡稱為一般說的「精度」。其間差異主要在於ISO5725 使用「真實度」(Trueness)替代原本的準確度(Accuracy)(圖5)。
「精度」為真實度與精密度的組合,包含受到偶然與系統兩部分誤差的影響,實務上,以被認可的參考值視為真值。ISO5725 以類同於圖3、圖1的彈著分布圖說明「精度」、真實度、精密度之間的關係(圖6)。
更多討論請見 地籍測量 第 32 卷第 3 期,第 18-26 頁: 史天元著 “準確度與精密度“
您好
有個地方不知道是不是我的誤解
相對誤差的定義就我知道的應該是
相對誤差=(實驗值-理論值)/理論值
換成文章內的代號應為(Xt-X)/X
與文章(X-Xt)/Xt,分母的部分並不相同