水的三相點不止一個

水的三相點不止一個
國立臺灣師範大學化學系兼任教師邱智宏

高中化學課程介紹相圖(phase diagram)時，常以大家耳熟能詳的「水」開始，探討其在不同溫度、壓力下的狀態變化。然而水的相圖，卻非常態，而是少數的例外，大多數純物質的相圖和水的長相不同，因此如何理解其不同的原因，便顯得格外重要。另外，水在高壓時的相圖卻甚少提到，其性質與低壓的情況是否相同？有没有 $$100^\circ C$$ 的冰？水的三相點僅有一個嗎？

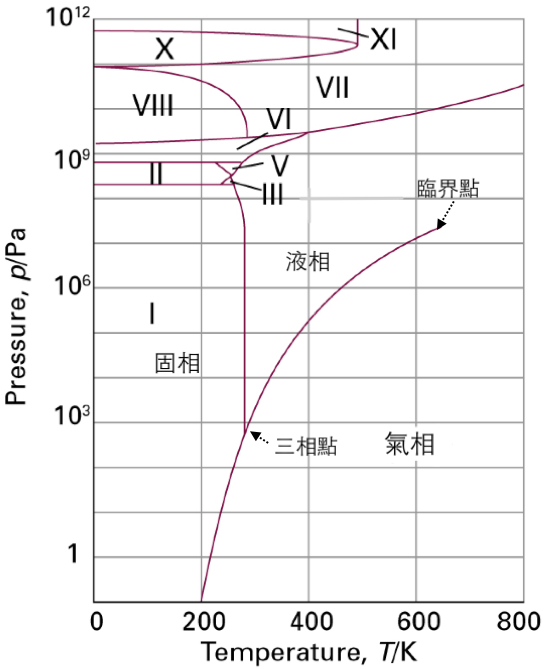
一般高中教科書中有關水的相圖，其壓力僅顯示約在 $$10^8~Pa$$ 以下的範圍
（$$1~atm=1.01\times 10^5~Pa$$）以觀察其不同溫度及壓力下，狀態的改變情況。圖一為水在更大壓力範圍下的相圖，恰恰在 $$10^8~Pa$$ 以上，水的相圖有著精彩的發展，在高壓的範圍內，冰的固體存在各種不同的結構，除常見的冰I以外，尚有冰II、冰III、冰V⋯等共八種。

圖一、水的相圖，Y 軸使用對數座標

首先，水的相圖和其他純物質最大的不同，即壓力在 $$10^8~Pa$$ 以下時，其固液共存線（熔點線）非常陡峭，而且向左傾斜，亦即斜率為負。其他大部分的物質斜率為正，其原因說明如下：

當同一物質的 $$\alpha,\beta$$ 兩相達到平衡時，其化學能(chemical potential，$$\mu$$)相等:

$$\mu_\alpha(p,T)=\mu_\beta(p,T)~~~~~~~~~(1)$$

由熱力學的基本公式得知 $$d\mu=-S_mdT+V_mdp$$，
其中 $$S_m,V_m$$ 為物質的莫耳熵(molar entropy)和莫耳體積，將此式代入 $$(1)$$ 式

$$-S_{\alpha,m}dT+V_{\alpha,m}dp=-S_{\beta,m}dT+V_{\beta,m}dp$$

$$(V_{\alpha,m}-V_{\beta,m})dT=(S_{\alpha,m}-S_{\beta,m})dp$$

$$\displaystyle\frac{dp}{dT}=\frac{\Delta S_m}{\Delta V_m}~~~~~~~~~(2)$$

式 $$(2)$$ 稱為克拉伯隆方程式(Clapeyron equation)，
其中 $$\Delta S_m$$ 為兩相間莫耳熵的差，而  $$\Delta V_m$$ 為兩相間莫耳體積的差。

在固-液兩相中，液相的莫耳熵（或亂度）顯然比固相為大(分子在固相中的排列較整齊，亂度小)，$$\Delta S_m$$ 為正值。一般情況下，液相的莫耳體積也比固相大，所以 $$\Delta V_m$$ 亦為正值，因此由式 $$(2)$$ 壓力隨溫度改變的量（即斜率）為正值，在相圖中熔點線，隨壓力的增加，熔點亦隨之上升。

圖二、冰I中的水分子由於氫鍵的作用，形成較不緊實的六方形結構，密度變小，圖中紅色球為氧原子，白色球為氫原子

另外，由於液相和固相的體積相差甚微，因此依據式 $$(2)$$ 所畫的線段斜率很大，即其線段很陡峭，而且是向右傾斜。

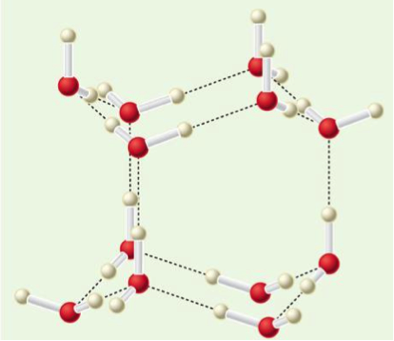
然而在 $$\mathrm{H_2O}$$ 的情形則不一樣，冰I的結構如圖二所示，固相的水分子之間，存在許多氫鍵，形成較不緊實的六方結構，熔解形成液相時，部分氫鍵破壞，造成液相的體積比固相小，因此 $$\Delta V_m$$ 為負值，即式 $$(2)$$ 的斜率為負。

顯然這個小小的異常現象，即加熱使冰熔解，體積反而增大，對自然界非常重要。因為它就是造成冰塊會浮於水上、嚴冬湖海的結冰由表面開始、水底生物不致滅絕的主要原因。

圖三、冰VI中的水分子在壓力增大時，形成較緊實的結構，密度變大

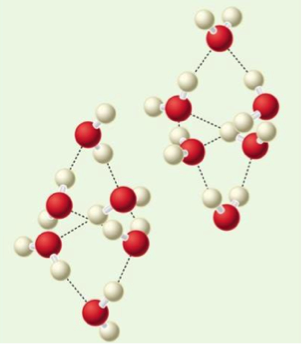
其次由圖一水的相圖可以看出，當壓力在 $$10^8~Pa$$ 以上時，冰會出現多種不同的結構，例如冰VI的結構如圖三所示，當壓力升至 $$10^9~Pa$$ 附近時，其間水分子重新調整結構，部分氫鍵消失，形成比冰I更為緊實的結構，密度增大，其固液相共存線的斜率也由負變正，即壓力加大時，熔點上升，這個情況和低壓的情形完全不同。由圖中可看出在高壓下，將出現在 $$100^\circ C$$（即 $$373.15~K$$）才熔解的冰。

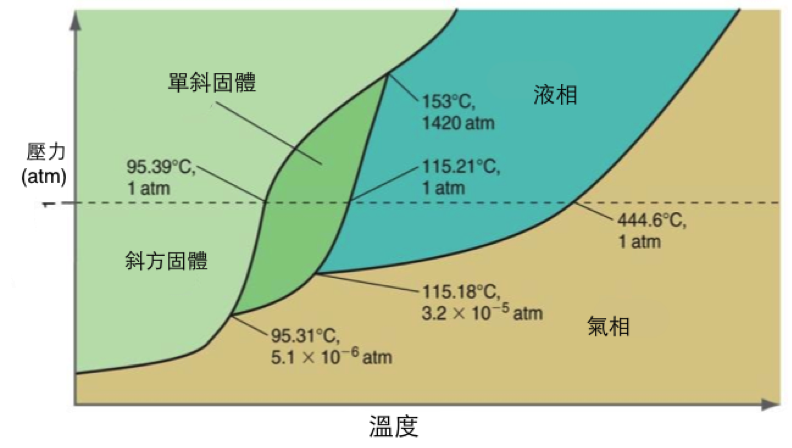
另外，水的三相點，除了(液)(固)(氣)三相共存的點以外，尚有許多(固$$\alpha$$)(固 $$\beta$$)(液)三相共存的點，即水的三相點並不只有一個。顯然許多純物質均存在數個三相點，例如圖四中硫的相圖，就有三個三相共存的點，其中二個出現在 $$1~atm$$ 以下。由相圖中可看出，在 $$1~atm$$ 時，斜方硫在低溫時較穩定，當溫度升高至 $$95.39^\circ C$$ 時，開始轉變成單斜硫，溫度繼續升高至 $$115.21^\circ C$$，固相開始熔化成為液體。通常在相圖中，三相點可能不是只有一個點，但是各純物質的臨界點(critical point )，可是獨特唯一的一個點。

圖四、硫的相圖，其中出現 $$3$$ 個三相點，$$2$$ 個在 $$1~atm$$ 以下

參考資料

1. http://www2.chem.uic.edu/tak/chem34013/Chem%20340%20-%20Notes%209.pdf
2. P. W. Atkins, “Physical Chemistry”, Oxford University Press, Oxford, 5th ed., p. 186~200 (1994).
3. 葉名倉，劉如熹，邱智宏，周芳妃，陳建華，陳偉民，高級中學化學選修上冊，南一書局，第121頁，2013 年。