條件機率(1)：定義（Conditional Probability (1)：Definition）

條件機率(1)：定義（Conditional Probability (1)：Definition）
臺北市立第一女子高級中學蘇俊鴻老師

條件機率(Conditional Probability)，如同字面意義，是在假設某事件發生的條件下，考慮原本事件發生的機率。例如，投擲公正硬幣兩次，出現兩次正面的機率為 \(\frac{1}{4}\)。若我們加上「已知第一次擲出正面」的條件的話，那麼出現兩正面的機率將變成 \(\frac{1}{2}\)。事實上，若是掌握條件機率的定義，倒也不難理解箇中變化：

設 \(A,B\) 為兩事件且 \(P(A)>0\)。
在事件 \(A\) 發生的情況下，事件 \(B\) 發生的機率的條件機率，以 \(P(B|A)\) 表示，
且定義 \(\frac{P(A\cap B)}{P(A)}\)。

設第一次擲出正面的事件為 \(A\)，出現兩正面的事件為 \(B\)。那麼，投擲公正硬幣兩次的樣本空間 \(S=\{\)正正，正反，反正，反反\(\}\)，\(A=\{\)正正，正反\(\}\)，\(B=\{\)正正\(\}\)，\(A\cap B=\{\)正正\(\}\)。

因此，\(P(A)=\frac{2}{4}=\frac{1}{2}\)，\(P(B)=\frac{1}{4}\)，\(P(A\cap B)=\frac{1}{4}\)，
故 \(P(B|A) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{{{\textstyle{1 \over 4}}}}{{{\textstyle{1 \over 2}}}} = \frac{1}{2}\)。

讓我們改變上述問題的條件，再來練習條件機率：

投擲公正硬幣兩次。在已知擲出一次正面的情形下，求投擲兩次皆為正面的機率。

延續上述的符號，並且設擲出一次正面的事件為 \(C\)，則 \(C=\{\)正正，正反，反正\(\}\)，\(A\cap C=\{\)正正\(\}\)。因此，\(P(B|C) = \frac{{{\textstyle{1 \over 4}}}}{{{\textstyle{3 \over 4}}}} = \frac{1}{3}\)。

換言之，在條件的影響下，事件的機率通常會產生變化。並且，不同的條件常常造成機率的改變，這使得原本懼怕機率的同學常覺得條件機率更是「難以掌握」。進一步，依據古典機率的定義，我們可以推得

\(\displaystyle P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{{\frac{{n\left( {A \cap B} \right)}}{{n\left( S \right)}}}}{{\frac{{n\left( A \right)}}{{n\left( S \right)}}}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( A \right)}}\)

式中 \(\frac{{n\left( {A \cap B} \right)}}{{n\left( A \right)}}\)比值的意義是：

將樣本空間「限縮」在事件 \(A\) 上，考慮事件 \(B\) 發生的機率，
此一詮釋符合條件機率的意涵，也呼應古典機率的定義。

不妨再回頭檢視上述提及的問題，更能確定此一詮釋的正確性：

\(A=\{\)正正，正反\(\}\)，\(A\cap B=\{\)正正\(\}\)，所以 \(P\left( {B|A} \right) = \frac{{n\left( {A \cap B} \right)}}{{n\left( A \right)}} = \frac{1}{2}\)；\(C=\{\)正正，正反，反正\(\}\)，\(A\cap C=\{\)正正\(\}\)，因此 \(P\left( {B|C} \right) = \frac{{n\left( {A \cap C} \right)}}{{n\left( C \right)}} = \frac{1}{3}\)。

事實上，「限縮樣本空間」的看法，常能幫忙我們解決情況較為複雜的條件機率問題，例如99年數甲的問題：

一個抽獎活動依排隊順序抽獎，輪到抽獎的人有一次抽獎機會，抽獎方式為丟擲一枚公正銅板，正面為中獎，反面為沒中獎。獎品有三份，活動直到三份獎品都被抽中為止，則在排第四位的人可以抽獎的情況下，排第五位的人可以抽獎的條件機率為何？

解法一：

令第四位可抽獎的事件為 \(A\)，第五位可抽獎的事件為 \(B\)，
由於第四位可抽獎，表示前三位的丟擲情形有下列三種
情形(1)：二正面一反面，機率為 \(C_1^3{(\frac{1}{2})^3} = \frac{3}{8}\)；
情形(2)：一正面二反面，機率為 \(C_2^3{(\frac{1}{2})^3} = \frac{3}{8}\)；
情形(3)：三個反面，機率為 \(C_3^3{(\frac{1}{2})^3} = \frac{1}{8}\)；
機率 \(P(A) = \frac{3}{8} + \frac{3}{8} + \frac{1}{8} = \frac{7}{8}\)。
接下來，第五位可以抽獎的狀況：若是情形(1)，第四位需丟擲反面；情形(2)(3)，第四位任意丟擲皆可。
因此，\(P(A \cap B) = \frac{3}{8} \times \frac{1}{2} + \frac{3}{8} \times 1 + \frac{1}{8} \times 1 = \frac{{11}}{{16}}\)，
故 \(P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{{\frac{{11}}{{16}}}}{{\frac{7}{8}}} = \frac{{11}}{{14}}\)。

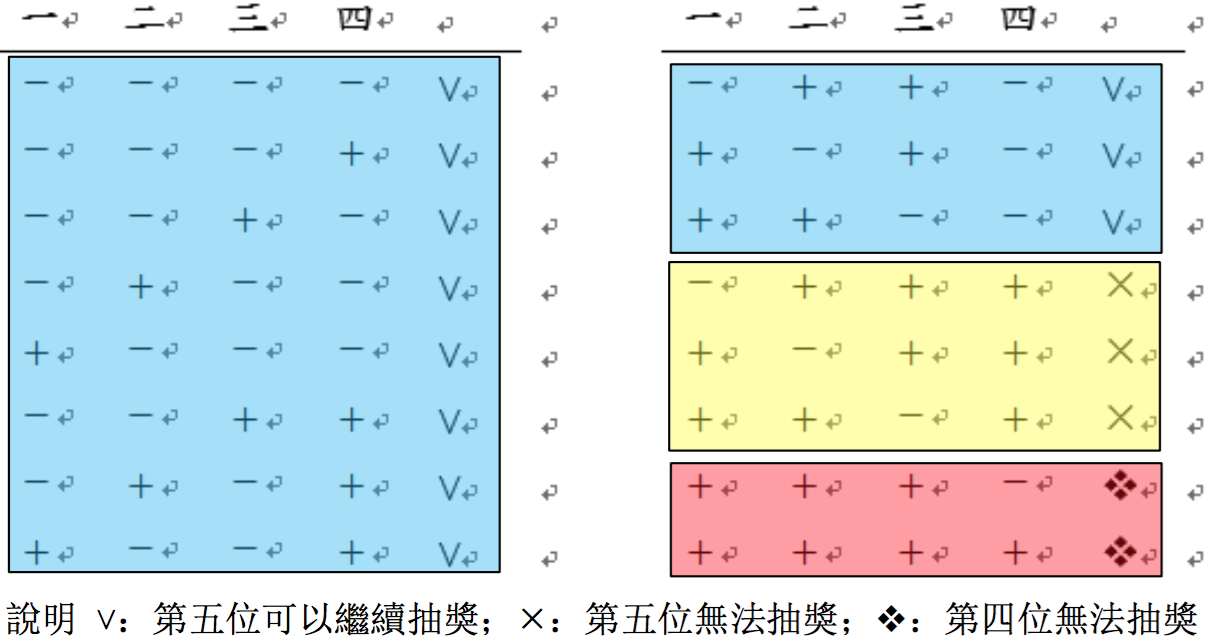
解法二：如下圖，我們將前面四位的各種抽獎情形列出，為了便於表示，丟擲正面以 \(+\) 表示；丟擲反面以 \(-\) 表示。

由圖易知，藍色和黃色部份表示第四位能抽獎的情形，共有 \(14\) 種。

其中，藍色為第五位能繼續抽獎的情形，有 \(11\) 種。因此，\(P\left( {B|A} \right) = \frac{{n\left( {A \cap B} \right)}}{{n\left( A \right)}} = \frac{{11}}{{14}}\)。

你看解法二是不是比解法一來得直接易懂呢！

不過，是否從此就能踏上解決條件機率問題的坦途？那倒也未必，請看102年學測的問題：

袋子裡有 \(3\) 顆白球，\(2\) 顆黑球。由甲、乙、丙三人依序各抽取顆球，抽取後不放回。若每顆球被取出的機會相等，請問在甲和乙抽到相同顏色球的條件下，丙抽到白球之條件機率為何？ (1) \(\frac{1}{3}\) (2)\(\frac{5}{12}\) (3) \(\frac{1}{2}\) (4) \(\frac{3}{5}\) (5) \(\frac{2}{3}\)

或許你是這麼想的：由於抽球的情形不是白就是黑，因此，甲乙兩人抽出同色球的事件集合為 \(\{\)白白白，白白黑，黑黑白\(\}\)。因此，在甲和乙抽到相同顏色球的條件下﹐丙抽到白球的條件機率為 \(\frac{2}{3}\)，答案為(5)。可惜的是，這題的正確解答為(3)，為什麼？若你是依循上述思路的話，請試著想想失落的環節是什麼，在下一篇文章〈條件機率(2)：乘法定律〉中將會提出說明。

連結：條件機率(2)：乘法定律