期望值(Expected Value)
期望值(Expected Value)
臺北市立第一女子中學數學科蘇俊鴻老師
如果想要粗略估計隨機變數 \(X\) 的大小,期望值 \(E(X)\) 是一個常用的代表。
而期望值定義是:
若隨機變數 \(X\) 的機率分布如下
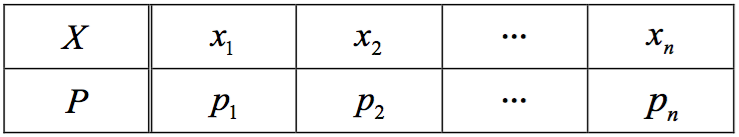 則隨機變數 X 的期望值 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \)
則隨機變數 X 的期望值 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \)
換言之,隨機變數 \(X\) 的期望值是 \(X\) 的所有可能值的加權平均數。
在期望值的單元中,常有下列的問題:
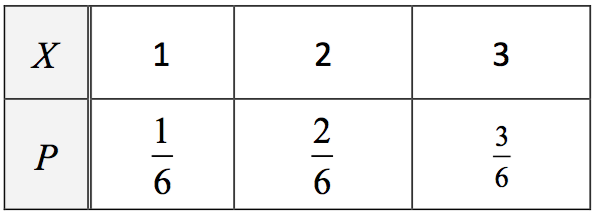
袋中裝有6張大小形狀相同的卡片,編號1號的有1張,2號有2張,3號有3張。
自袋中一次取出卡片1張,若卡片上的編號即為所得分數,求得分的期望值。
解法如下
令 \(X\) 為抽出卡片的得分,可能取值為 \(1,2,3\),其機率分布為
期望值 \(E(X) = 1 \times \frac{1}{6} + 2 \times \frac{2}{6} + 3 \times \frac{3}{6} = \frac{{1 + 4 + 9}}{6} = \frac{{14}}{6} = \frac{7}{3}\)
只要依照期望值的定義,就能順利求得答案。
不過,若將問題進一步延伸為
自袋中一次取出卡片2張,若卡片上的編號即為所得分數,求得分和的期望值。
事實上,遵循期望值的定義依然可解
令 \(X\) 為抽出卡片的得分和,可能取值為 \(3,4,5,6\),其機率分布為
期望值 \(E(X) = 3 \times \frac{2}{{15}} + 4 \times \frac{4}{{15}} + 5 \times \frac{6}{{15}} + 6 \times \frac{3}{{15}} = \frac{{70}}{{15}} = \frac{{14}}{3}\)
然而,通常高中教師還會再進一步提供速解:由於取出 \(1\) 張卡片的期望值為 \(\frac{7}{3}\),因此,取出 \(2\) 張卡片的期望值為 \(2\times \frac{7}{3}=\frac{14}{3}\)。儘管答案總是正確,但仔細思量常有不安之感。若是取 \(2\) 張卡片的方式為取完 \(1\) 張放回,再取 \(1\) 張,兩次動作彼此是獨立的,上述解法就顯得自然而然。不過,若是一次取出 \(2\) 張的話,為何仍然會成立呢?
事實上,這個結果是恆成立,因為機率論告訴我們:
當兩個隨機變數 \(X,Y\) 不相互獨立時,\(E(X+Y)=E(X)+E(Y)\) 仍然成立。
下面就用離散型隨機變數為例說明:
設 \(X,Y\) 為兩個離散型隨機變數,
其結合機率質量函數為 \(P(X = {x_i},Y = {y_j})\),\(i,j=1,2,3,\cdots\)
則 \(P(X = {x_i}) = \sum\limits_j {P(X = {x_i},Y = {y_j})} \);\(P(Y = {y_j}) = \sum\limits_i {P(X = {x_i},Y = {y_j})} \)
因此,\(\begin{array}{ll}E(X + Y) &= \sum\limits_i {\sum\limits_j {({x_i} + {y_j})P(X = {x_i},Y = {y_j})} }\\&= \sum\limits_i {\sum\limits_j {{x_i}P(X = {x_i},Y = {y_j})} }+\sum\limits_i {\sum\limits_j {{y_j}P(X = {x_i},Y = {y_j})} } \\&= \sum\limits_i {{x_i}\sum\limits_j {P(X = {x_i},Y = {y_j})} }+ \sum\limits_j {{y_j}\sum\limits_i {P(X = {x_i},Y = {y_j})} }\\&=\sum\limits_i {{x_i}P(X = {x_i}) + } \sum\limits_j {{y_j}P(Y = {y_j}) = E(X) + E(Y)} \end{array}\)
換言之,離散型隨機變數期望值的本質是和分,至於連續型隨機變數期望值的本質則是積分,故加性(additivity)都會繼續成立,不會受到隨機變數有無獨立的影響。
事實上,這個性質也能推廣到 \(X_1,X_2,\cdots,X_n\) 為 \(n\) 個隨機變數,
則有 \(E({X_1} + {X_2}+\cdots+{X_n})= E({X_1})+E({X_2})+\cdots+E({X_n})\)。


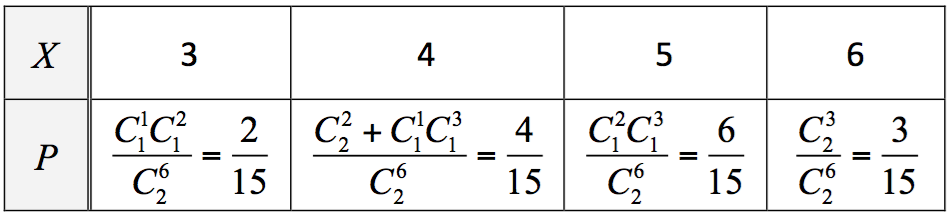
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
