有效的使用表列的熱力學數據－以水蒸氣為例

有效的使用表列的熱力學數據－以水蒸氣為例 (Effective use of tabulated thermodynamic data – a case study in water vapor)
國立臺灣師範大學化學系兼任教師邱智宏

能適切的預測一個化學反應的熱力學數據是非常有用的技巧，這些數據包括反應焓 (reaction enthalpy)、自由能 (Gibbs free energy)、熵 (entropy)及定壓熱容量 (heat capacity) 等，它們可以用來預判反應能否自發進行？藉以推估平衡常數及標準還原電位的大小，也可以用於規劃反應進行的最佳條件，因此一般化學教科書均會將一些常見物質在 $$298.15~K$$、$$1~bar$$ 的相關數據，表列在附錄中，以供參考及使用。

但是這些數據應該如何正確、有效的使用？卻鮮少被討論，尤其是不同溫度時，如何利用表列中現有的數據，預估或計算熱力學數據的變化，更是學子們應熟稔的技巧，本文擬以氫氣及氧氣生成水蒸氣的化學反應為例子，說明如何利用表列的數據，求出此反應的反應焓、自由能及熵，也利用熱容量計算出不同溫度下上述熱力學數據的變化情形。

一、標準狀態的定義及參考狀態的選擇

一般列表的熱力學數據，均有其訂定的標準狀態(standard state)，通常為 $$1~bar$$ 下的某特定溫度，此溫度若為 $$25^\circ C$$，則以 $$H^\circ_{m,298}$$ 表示在 $$298.15~K$$ 的標準莫耳相對焓，其中上標 $$\circ$$ 表示標準壓力為 $$1~bar$$，下標的 $$m$$ 表示單位莫耳。而 $$S^\circ_{m,0}$$ 則表示在 $$0~K$$ 時標準莫耳相對熵，另外，若純物質為氣態，則假定在標準狀態其為理想氣體，而非真實氣體。

熱力學的第二定律可以計算出純物質焓及熵的變化量，卻無法告訴我們絶對的焓及熵，因此必需了解學術界如何定義相對焓及熵。從相對焓的部分開始，首先必需選擇在某特定參考狀態(reference state)下，所有在最穩定狀態的元素，其相對焓均為 $$0$$，再測量出由特定狀態到欲求狀態的焓值變化量。對於焓而言，選擇 $$1~bar$$、$$298.15~K$$ 是最方便的參考狀態，即對所有元素在其最穩定的狀態時規定其 $$H^\circ_{m,298}$$。

有多種同素形體時，則以最常見或最重要的同素異形體訂為 $$0$$，例如碳、硫、磷、氧的異形體中則分別以石墨、斜方硫、白磷(黃磷)、$$\mathrm{O_2}$$ 的元素訂為 $$0$$。將各種不同的元素的標準相對焓均隨意設為 $$0$$，並不會造成計算上的錯誤，因為化學反應進行時，不同元素間並不會互相轉換。

熵的情況則不一樣，其參考狀態為 $$1~bar$$、$$0~K$$，由熱力學第三定律得知各元素和化合物的相對熵均為 $$0$$，即 $$S^\circ_{m,0}=0$$，因此一般表列各物質的 $$S^\circ_{m,0}\ne 0$$，必須實際量測從 $$0$$ 到 $$298.15~K$$ 時熵的變化量。至於標準莫耳相對自由能 $$(G^\circ_{m,298})$$ 的部可透過相對焓及熵求出。

現以溫度為 $$298.15~K$$ 時由氫氣及氧氣生成 $$1$$ 莫耳水蒸氣為例，說明如何求出其標準莫耳反應熵、自由能及熵。

$$\displaystyle\mathrm{ H_{2(g)}+\frac{1}{2}O_{2(g)}\rightarrow H_2O_{(g)}~~~~~~~~~(1)}$$

上式的反應焓$$(\Delta_r H^\circ_{m,T})$$正好也是水蒸氣的莫耳生成焓$$(\Delta_r H^\circ_{m,T}\mathrm{H_2O_{(g)}})$$，可透過下式求出，即生成物的莫耳相對焓乘以相對應係數，減去反應物的莫耳相對焓乘以相對應係數：

$$\Delta_rH^\circ_{m,T}=1\times H^\circ_{m,T}\mathrm{(H_2O_{(g)})}-1\times H^\circ_{m,T}\mathrm{(H_2)}-\frac{1}{2}\times H^\circ_{m,T}\mathrm{(O_{2(g)})}~~~~~~~~~(2)$$

透過網站查表，可得溫度為 $$298.15~K$$ 時，上列各物種的各項熱力學數據，詳如表一。

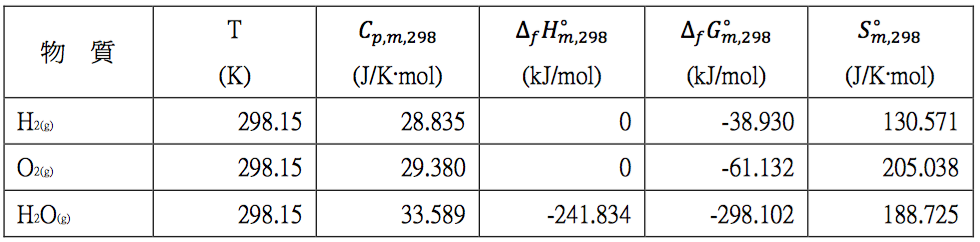
表一$$~~~$$查表在 $$298.15~K$$，$$1~bar$$ 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據 （作者整理）

將表一的焓值代入 $$(2)$$ 式，可得：

$$\Delta_r H_{m,298}^\circ=H_{m,298}^\circ(\mathrm{H_2O_{(g)}})-0-\frac{1}{2}\times 0=-241.834~kJ/mol$$

由上式可以看出在參考狀態時，即溫度為 $$298.15~K$$ 時，類似 $$(1)$$ 式的生成反應，因為各反應物均為元素，依規定其相對焓都訂為 $$0$$，此時的莫耳反應焓亦為莫耳生成焓，也等於該生成化合物的莫耳相對焓 $$H_{m,298}^\circ (\mathrm{H_2O_{(g)}})$$。

若溫度不是 $$298.15~K$$ 時，各元素物質的相對焓不為 $$0$$，此時的莫耳生成焓亦不等於該生成物的莫耳相對焓。習慣上，在參考狀態時的列表數據，均將莫耳相對焓、莫耳相對自由能以莫耳生成焓 $$(\Delta_f H^\circ_{m,298})$$、莫耳生成自由能 $$(\Delta_f G^\circ_{m,298})$$ 表示。

二、不同溫度下，標準莫耳反應焓、自由能及熵的算法

標準反應自由能及標準反應熵的計算方法亦和反應焓一樣：

$$\Delta_r G_{m,298}^\circ=(-298.102)-(-38.930)-\frac{1}{2}\times (-61.132)=-228.606~kJ/mol$$

$$\Delta_r S_{m,298}^\circ=(188.725)-(130.571)-\frac{1}{2}\times (205.038)=-44.362~kJ/mol$$

當反應的溫度不是參考狀態時，例如是 $$400~K$$ 時，是否也能利用參考狀態的數據，求出相關的數據。首先可以利用表一中給的定壓熱容量，透過下式求出不同溫度下的相對焓，及相對熵

$$\displaystyle H_{m,400}^\circ=H_{m,298}^\circ+\int_{298}^{400}C_{p,m,298}\mathrm{d}T~~~~~~~~~(3)$$

$$\displaystyle{S_{m,400}^\circ}=S_{m,298}^\circ+\int_{298}^{400}\frac{C_{p,m,298}}{T}\mathrm{d}T~~~~~~~~~(4)$$

上二式中的熱容量隨溫度改變的量甚小，在溫度改變不大時，可視為定值，因此上二式可改寫成：

$$H_{m,400}^\circ=H_{m,298}^\circ+C_{p,m,298}\times (400-298.15)~~~~~~~~~(5)$$

$$S_{m,400}^\circ=S_{m,298}^\circ+C_{p,m,298}\times \ln\frac{400}{298.15}~~~~~~~~~(6)$$

將表一的相關數代入 $$(5)$$、$$(6)$$ 兩式，並利用求出的相對焓及熵代入下式，求出相對自由能，其結果詳如表二。

$$G_{m,400}^\circ=H_{m,400}^\circ-T\times S_{m,400}^\circ~~~~~~~~~(7)$$

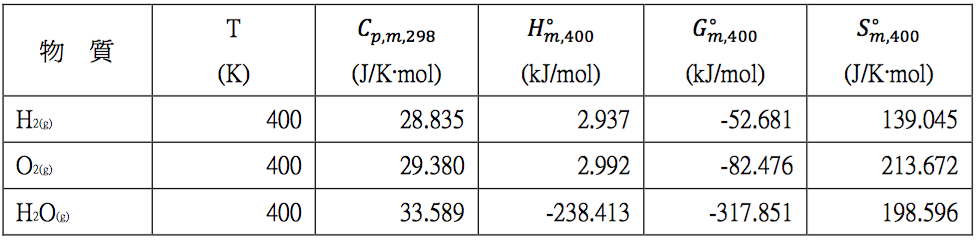
表二$$~~~$$計算在 $$400~K$$，$$1~bar$$ 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據 （作者整理）

利用表二可以計算 $$(1)$$ 式在 $$400~K$$ 的反應焓、自由能及熵：

$$\Delta_r H_{m,400}^\circ=(-298.413)-(2.937)-\frac{1}{2}\times (2.992)=-242.846~kJ/mol$$

$$\Delta_r G_{m,400}^\circ=(-317.851)-(-52.681)-\frac{1}{2}\times (-82.476)=-223.932~kJ/mol$$

$$\Delta_r S_{m,400}^\circ=(198.596)-(139.045)-\frac{1}{2}\times (213.672)=-47.285~kJ/mol$$

我們將再透過相同網站查表，所得數據如表三。

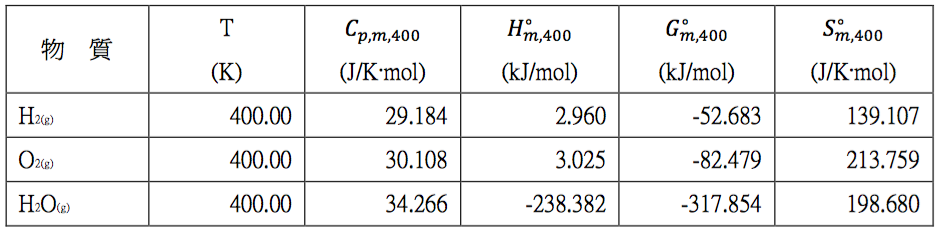
表三$$~~~$$查表在 $$400~K$$，$$1~bar$$ 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據 （作者整理）

利用表三查表所求出的相關數據和利用表一所得的計算值相互比較，其結果整理表四。由表中可看出其相對誤差幾乎可勿略不計。另外，由表二在 $$298.15~K$$ 時各物種之定壓熱容量和表三在 $$400~K$$ 時之相對應的熱容量比較，其誤差約為 $$3~\%$$，例如水蒸氣在 $$298.15~K$$ 時為 $$33.589$$，和 $$400~K$$ 時的 $$34.266$$ 比較，兩者相差不到 $$2~%$$，因此將熱容量視為定值，亦屬合理的範圍。

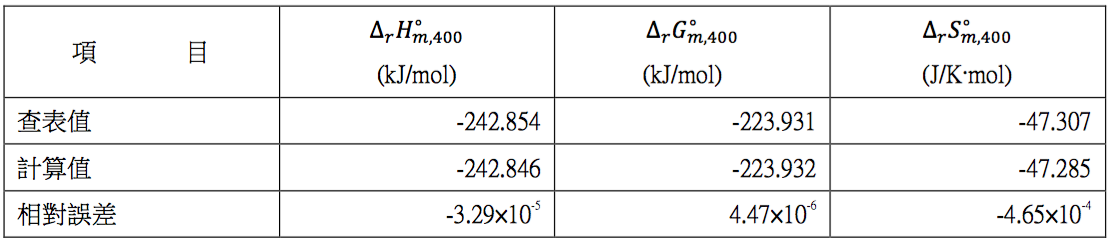
表四$$~~~$$在 $$400~K$$，$$1~bar$$ 下 $$\mathrm{H_2}$$ 及 $$\mathrm{O_2}$$ 生成 $$\mathrm{H_2O}$$ 的熱力學數據查表值及計算值的比較 （作者整理）

四、結論

本文利用水蒸氣的莫耳生成反應為例，說明如何利用一般列表的熱力學數據，求出標準反應焓、反應自由能及反應熵。由上述的討論可知，在參考狀態時，化合物的莫耳生焓即等於該化合的莫耳相對焓。但在不同溫度時，則没有相等的關係。另外，表列的數據一定附有定壓熱容量的數據，在溫度改變範圍不大時，將其視為定值，可以利用它來計算不同溫度下的反應焓、反應自由能及反應熵，其誤差幾乎可以忽略不計。若要計算溫度改變很大的情形，則必須得知熱容量和溫度間的關係式，將其代入 $$(3)$$、$$(4)$$ 式中確實進行積分，才能得到正確的結果。

參考文獻

1. Levine, I. N.(1988), Physical Chemistry (3rd ed.). p211~225, McGRAW-HILL Book Company.
2. Jacobson, N. (2001), Use of tabulated thermochemical data for pure compounds, Journal of Chemical Education, 78, 814~819.
3. 標準狀況下理想氣體與真實氣體間的熵值差－以SO₂為例 — 高瞻計畫資源平台，/highscope/?s=邱智宏