數學期望值
數學期望值 (Mathematical Expectation)
國立屏東高級中學數學科楊瓊茹老師
在處理有關財務風險的事務時,不免要衡量可能的得與失,「數學期望值」的觀念在此時就顯得特別重要,可以幫助我們思考及判斷出最佳的決策。其定義如下:
若隨機變數 \(X\) 的機率分布如下表﹕
則稱 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \) 為隨機變數 \(X\) 的數學期望值。
數學期望值 (簡稱期望值) 即平均值的概念,而且是加權平均數。將每個結果依它發生的機率來加權,發生機率愈大,權數愈高。
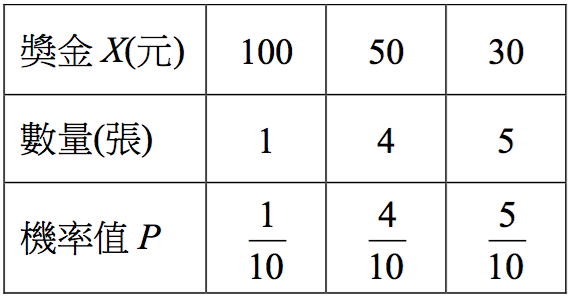
舉例來說,參加一摸彩遊戲,抽獎箱裡放置了三種分別標有獎金100元、50元、30元的彩券共10張,其中100元有1張、50元有4張和30元有5張。參賽者繳交55元可摸取一張彩券,假設每張彩券被抽出的機率都相同。那麼,平均每張彩券的獎金是:\(\frac{{{\rm{100}} \times {\rm{1}} + {\rm{20}} \times {\rm{4}} + {\rm{30}} \times {\rm{5}}}}{{{\rm{10}}}} = {\rm{45}}\) (元)。
上列算式也可用機率的觀點解釋每張彩券的價值,假設隨機變數 \(X\) 為可能抽到的獎金,相對應發生的機率值 \(P\) ,\({\rm{100}} \times \frac{{\rm{1}}}{{{\rm{10}}}} + {\rm{50}} \times \frac{{\rm{4}}}{{{\rm{10}}}} + {\rm{30}} \times \frac{{\rm{5}}}{{{\rm{10}}}} = {\rm{45}}\)(元),即獎金乘上其機率值,再將這些乘積全部加起來,我們稱之為獎金的期望值。不過,參加一次遊戲就要先付55元,雖然獎金期望值有45元,但參賽者每玩一次預期要虧損10元。
另外,期望值在保險上的應用也值得討論,例如:保險公司推出一年期壽險﹐保險額200萬元,保費230元。若統計資料顯示一年內死亡的機率為0.0001,則保險公司每一份保單的預期理賠金額 \({\rm{2,000,000}} \times {\rm{0.0001}} = {\rm{200}}\)元,比230元保險費低,有利潤期望值30元。似乎保險公司賣愈多保單,獲利愈豐厚,而你付了230元,買到價值200元的風險,只有傻瓜才會做賠本生意?其實,當遭逢變故時所得到的保險理賠,比起多付30元的保費,是把支撐家人免於處境艱困的保護傘。
這其中得與失的平衡,必須自己決定!底下,我們來回顧歷史上著名的「巴斯卡賭注」( Pascal’s Wager),巴斯卡如何思考「上帝存在」和「上帝不存在」 這兩個命題?如何衡量信奉上帝的得與失?
“God is, or He is not.” But to which side shall we incline? Reason can decide nothing here. There is an infinite chaos which separated us. A game is being played at the extremity of this infinite distance where heads or tails will turn up. What will you wager?……..Since you must choose, let us see which interests you least..……. Let us weigh the gain and the loss in wagering that God is. Let us estimate these two chances. If you gain, you gain all; if you lose, you lose nothing. Wager, then, without hesitation that He is. ……. Since there is an equal risk of gain and of loss,……. But there is here an infinity of an infinitely happy life to gain, a chance of gain against a finite number of chances of loss, and what you stake is finite.
究竟上帝存在還是不存在呢?我們應該傾向哪一邊?理智在此無法決斷,有一個無限的混沌世界將我們分隔。在無窮遠處,投擲錢幣的遊戲將開出正面還是反面,你賭哪一面?……。當你必須做出選擇時,就要看那一種對你影響最少。……。讓我們衡量賭上帝存在時可能的得與失,評估這兩個機率。如果你贏了,贏得一切;如果輸了,也沒什麼損失。那麼不必猶豫,就賭上帝存在吧!……。既然贏與輸有相同的風險,……。贏的機會相較於有限的失敗機會,這裡有無窮大的永恆快樂生活可以獲得,而你所押的賭注是有限的。
這是巴斯卡在其著作《沉思錄》(Pensée) 中的論述,這本書至今仍印行,台灣也有不少中譯本。巴斯卡對「無窮」有一定的了解,也知道將機率乘以報酬成為期望報酬,他將數學想法發揮在信仰上帝的問題上。也就是說,如果上帝存在(贏),你所得到的是無窮大的一半,如果上帝不存在(輸),你所損失的是一個有限賭注的一半,兩者合併起來,期望值仍是無限大。
參考資料
- 曼羅迪諾著、胡守仁譯(2012),《醉漢走路-機率如何左右你我的命運和機會》,台北:天下遠見出版社。
- 許志農主編(2013) ,《選修數學甲》上冊, 台北:龍騰文化。
- http://en.wikipedia.org/wiki/Pascal%27s_Wager


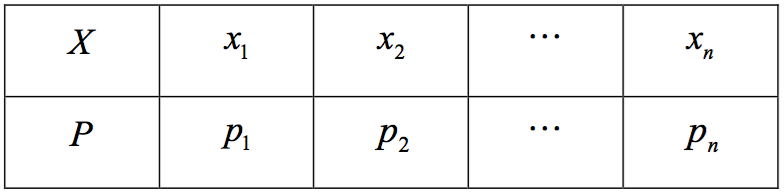
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
