數學之旅：三角形面積公式(Ⅳ)

Posted on 2016/02/18 in 向量幾何, 幾何, 數學 with 尚無留言 50,123 views

數學之旅：三角形面積公式(Ⅳ) (Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師

當數學旅程來到空間時，我們首先需要空間向量的外積(cross product)：兩空間向量 \(\vec{a} = \left( {{x_1},{y_1},{z_1}} \right),\vec{b} = \left( {{x_2},{y_2},{z_2}} \right)\) 的外積定義為

\(\begin{array}{ll}\vec{n} &= \vec{a} \times \vec{b} = \left( {\left| {\begin{array}{*{20}{c}} {{y_1}}&{{z_1}}\\ {{y_2}}&{{z_2}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{z_1}}&{{x_1}}\\ {{z_2}}&{{x_2}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}\\ {{x_2}}&{{y_2}} \end{array}} \right|} \right) \\&= \left( {{y_1}{z_2} – {y_2}{z_1},{x_2}{z_1} – {x_1}{z_2},{x_1}{y_2} – {x_2}{y_1}} \right)\end{array}\)

外積有三個性質：

向量 \( \vec{n} = \vec{a} \times \vec{b} = \left( {{y_1}{z_2} – {y_2}{z_1},{x_2}{z_1} – {x_1}{z_2},{x_1}{y_2} – {x_2}{y_1}} \right)\) 分別與 \(\vec{a} = \left( {{x_1},{y_1},{z_1}} \right),\vec{b} = \left( {{x_2},{y_2},{z_2}} \right)\) 垂直。
證明：
\(\begin{array}{ll} \vec{n} \cdot \vec{a} &= \left( {{y_1}{z_2} – {y_2}{z_1},{x_2}{z_1} – {x_1}{z_2},{x_1}{y_2} – {x_2}{y_1}} \right) \cdot \left( {{x_1},{y_1},{z_1}} \right) \\&= \left( {{y_1}{z_2} – {y_2}{z_1}) \cdot {x_1} + ({x_2}{z_1} – {x_1}{z_2}) \cdot {y_1} + ({x_1}{y_2} – {x_2}{y_1}} \right) \cdot {z_1}\\ &= {x_1}{y_1}{z_2} – {x_1}{y_2}{z_1} + {x_2}{y_1}{z_1} – {x_1}{y_1}{z_2} + {x_1}{y_2}{z_1} – {x_2}{y_1}{z_1}\\ &= 0 \end{array}\)
同理，\(\vec{n}\cdot\vec{b}=0\)，得証。
向量 \(\vec{a} = \left( {{x_1},{y_1},{z_1}} \right),\vec{b} = \left( {{x_2},{y_2},{z_2}} \right),\vec{n}=\vec{a}\times\vec{b}\) 符合右手定則。
圖一作者陳敏晧繪，圖中的紅色向量即為 \(\vec{AB}\times \vec{AC}\)。
\(\vec{n}=\vec{a}\times\vec{b}\) 的長度就是向量 \(\vec{a},\vec{b}\) 所張出的平行四邊形面積，其等價證明如下。
求證：三角形面積公式 \(a\Delta ABC=\displaystyle\frac{1}{2}|\vec{AB}\times\vec{AC}|\)。
證明：
\(\begin{array}{ll}a\Delta ABC &= \frac{1}{2}\overline {AB}\cdot\overline{AC}\cdot\sin A \\&= \frac{1}{2}\sqrt {{{\overline {AB} }^2} \cdot {{\overline {AC} }^2} \cdot {{\sin }^2}A} \\&= \frac{1}{2}\sqrt {{{\left| {\vec{AB}} \right|}^2} \cdot {{\left| {\vec{AC}} \right|}^2} \cdot (1 – {\cos^2}A)} \\&= \frac{1}{2}\sqrt {{{\left| {\vec{AB}} \right|}^2} \cdot {{\left| {\vec{AC}} \right|}^2} – {{\left| {\vec{AB}} \right|}^2} \cdot {{\left| {\vec{AC}} \right|}^2}{\cos^2}A} \\&= \frac{1}{2}\sqrt {{{\left| {\vec{AB}} \right|}^2} \cdot {{\left| {\vec{AC}} \right|}^2} – {{\left( {\vec{AB} \cdot\vec{AC}} \right)}^2}} \\ &= \frac{1}{2}\sqrt {\left( {{x_1}^2 + {y_1}^2 + {z_1}^2} \right) \cdot \left( {{x_2}^2 + {y_2}^2 + {z_2}^2} \right) – {{\left( {{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}} \right)}^2}} \\ &= \frac{1}{2}\sqrt {{{\left( {{y_1}{z_2} – {y_2}{z_1}} \right)}^2} + {{\left( {{x_2}{z_1} – {x_1}{z_2}} \right)}^2} + {{\left( {{x_1}{y_2} – {x_2}{y_1}} \right)}^2}} \\ &= \frac{1}{2}\sqrt {{{\left| {\begin{array}{*{20}{c}} {{y_1}}&{{z_1}}\\ {{y_2}}&{{z_2}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{z_1}}&{{x_1}}\\ {{z_2}}&{{x_2}} \end{array}} \right|}^2} + {{\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}\\ {{x_2}}&{{y_2}} \end{array}} \right|}^2}} \\ &= \frac{1}{2}\left| {\left( {\left| {\begin{array}{*{20}{c}} {{y_1}}&{{z_1}}\\ {{y_2}}&{{z_2}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{z_1}}&{{x_1}}\\ {{z_2}}&{{x_2}} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}\\ {{x_2}}&{{y_2}} \end{array}} \right|} \right)} \right|\\ &= \frac{1}{2}\left| {\vec{AB} \times\vec{AC}} \right| \end{array}\)

圖二空間中三點A,B,C求面積，作者陳敏晧繪。

常見的題目如下：

已知空間中三點 \(A(1,2,3),B( – 1,0,1),C(0, – 1,t)\)，其中 \(t\in \mathbb{N}\)，若 \(\Delta ABC\) 面積為 \(2\sqrt{2}\)，求 \(t=\)_______ 。

解法：因為 \(\vec{AB}=(-2,-2,-2),\vec{AC}=(-1,-3,t-3)\)

又 \(\vec{AB} \times \vec{AC} = \left( {\left| {\begin{array}{*{20}{c}} { – 2}&{ – 2}\\ { – 3}&{t – 3} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} { – 2}&{ – 2}\\ {t – 3}&{ – 1} \end{array}} \right|,\left| {\begin{array}{*{20}{c}} { – 2}&{ – 2}\\ { – 1}&{ – 3} \end{array}} \right|} \right) = \left( { – 2t,2t – 4,4} \right)\)

\(\begin{array}{ll} a\Delta ABC &= \frac{1}{2}\left| {\vec{AB} \times\vec{AC}} \right| = \frac{1}{2}\sqrt {{{\left( { – 2t} \right)}^2} + {{\left( {2t – 4} \right)}^2} + {4^2}} \\&= \sqrt {{{\left( { – t} \right)}^2} + {{\left( {t – 2} \right)}^2} + {2^2}} \\ &= \sqrt {2{t^2} – 4t + 8} = 2\sqrt 2 \end{array}\)

，左右平方得：\(2t^2-4t+8=8\)，整理得 \(2t(t-2)=0\)，

所以，\(t=0,2\)，又 \(t\in \mathbb{N}~~~\therefore t=2\)。

最後，我們談一個特殊的三角形公式－Pick公式，它是在1899由奧地利數學家皮克(George Alexander Pick, 1859-1943)所提出的，他在1880年獲得博士學位，1884年在萊比錫大學(University of Leipzig)與德國數學家克萊因(Felix Christian Klein, 1849-1925)共事。

圖三取自https://en.wikipedia.org/wiki/Georg_Alexander_Pick

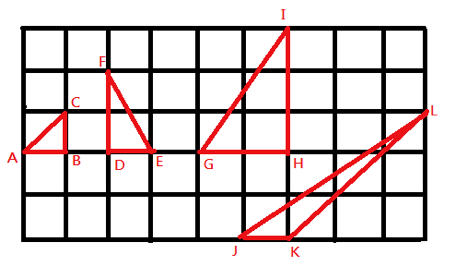
Pick公式：若多邊形(polygon)的每一個頂點都是格子點，且 \(i\) 為多邊形邊界上格子點個數，\(j\) 為多邊形內部格子點個數，則多邊形的面積為 \(\displaystyle\frac{i}{2}+j-1\)。[1]

圖四各種三角形，作者陳敏晧繪。

\(\begin{array}{l} a\Delta ABC = \frac{i}{2} + j – 1 = \frac{3}{2} + 0 – 1 = \frac{1}{2}\\ a\Delta DEF = \frac{i}{2} + j – 1 = \frac{4}{2} + 0 – 1 = 1\\ a\Delta GHI = \frac{i}{2} + j – 1 = \frac{6}{2} + 1 – 1 = 3\\ a\Delta JKL = \frac{i}{2} + j – 1 = \frac{5}{2} + 0 – 1 = \frac{3}{2} \end{array}\)

93年指考乙曾出現Pick公式的考題：

當平面上的點 \((x,y)\) 之坐標 \(x\) 與 \(y\) 都是整數時，稱點為格子點。數學家知道：坐標平面上三個頂點皆為格子點的三角形之面積可以用公式：\(aS+bI+c\) 來表示，其中 \(S\) 代表三角形三邊邊上的格子點數，\(I\) 是落在三角形內部(不含邊上)的格子點數，\(a,b,c\) 是固定的常數。則 \((a,b,c)=\)______。
答案：\((a,b,c)=(0.5,1,-1)\)。

讀者可以取三個不同類型的三角形，代入後，立三元一次聯立方程式，即可解出答案。

註：[1] Pick公式適用於計算多邊形面積，但是，本文僅聚焦於三角形面積。

參考文獻