反應焓的聯想（二）

反應焓的聯想（二）(Thoughts on reaction enthalpy (II))
國立臺灣師範大學化學系兼任教授 邱智宏

連結：反應焓的聯想（一）

現以溫度為 298.15 K 時由氫氣及氧氣生成 $$1$$ 莫耳水蒸氣為例，說明如何求出其標準莫耳反應焓，並藉以釐清反應焓、生成焓及相對焓的異同。

$$\displaystyle\mathrm{H_{2(g)}}+\frac{1}{2}\mathrm{O_{2(g)}}\rightarrow \mathrm{H_2O_{(g)}}~~~~~~~~~(5)$$

一般定義一莫耳純物質若由其成分元素經反應化合而成，則其焓的變化量稱為該物質的莫耳生成焓。由此定義可知，在參考狀態下元素的莫耳生成焓為 $$0$$，因為自己變成自己，焓並不會改變。在標準狀態下計算 $$(5)$$ 式化學反應的反應焓 $$(\Delta_rH^{\circ}_{m,T})$$ 即稱為標準莫耳反應焓，在此例中正好也是水蒸氣的莫耳生成焓 $$(\Delta_fH^{\circ}_{m,T}(\mathrm{H_2O_{(g)}}))$$，可透過下式求出，即生成物的莫耳相對焓乘以相對應係數，減去反應物的莫耳相對焓乘以相對應係數：

$$\Delta_rH^{\circ}_{m,T}=1\times H^{\circ}_{m,T}(\mathrm{H_2O_{(g)}})-1\times H^{\circ}_{m,T}(\mathrm{H_{2(g)}})-\frac{1}{2}\times H^{\circ}_{m,T}(\mathrm{O_{2(g)}})~~~~~~~~~(6)$$

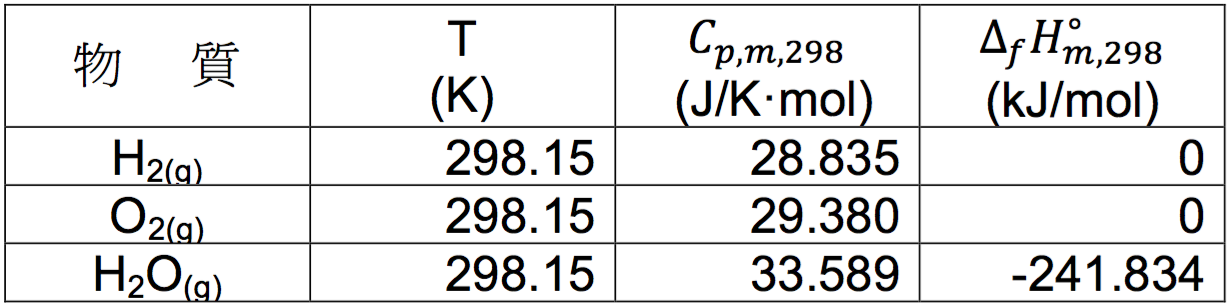
透過網站查表 (httl://www.crct.polymtl.cal/FACT/website.htm)，可得溫度為 298.15 K 時，上列各物種的各項熱力學數據，詳如表一。

表一 查表在 298.15 K，1 bar 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據。（作者整理製作）

將表一的焓值代入 $$(2)$$ 式，可得：

$$\displaystyle\Delta_rH^{\circ}_{m,298}=H^{\circ}_{m,298}(\mathrm{H_2O_{(g)}})-0-\frac{1}{2}\times 0=-241.834~kJ/mol$$

由上式可以看出在參考狀態時，即溫度為 298.15 K 時，類似 $$(5)$$ 式的生成反應，因為各反應物均為元素，依規定其相對焓都訂為 $$0$$，此時的莫耳反應焓已如上述，亦為莫耳生成焓，也等於該生成化合物的莫耳相對焓 $$(H^{\circ}_{m,298}(\mathrm{H_2O_{(g)}}))$$。若溫度不是 298.15 K 時，各元素物質的相對焓不為 $$0$$，此時的莫耳生成焓亦不等於該生成物的莫耳相對焓。習慣上，在參考狀態時的列表數據，均將莫耳相對焓以莫耳生成焓 $$(\Delta_fH^{\circ}_{m,298})$$ 表示。

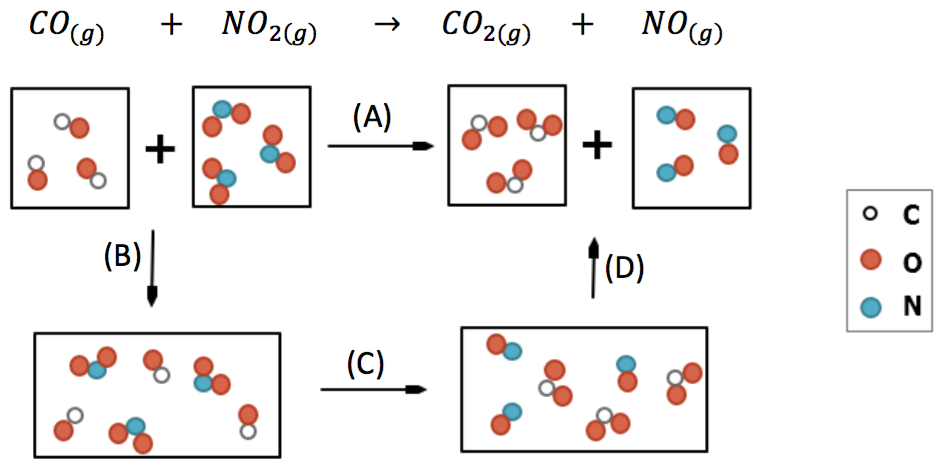
以上的說明，均認定各氣體物質為理想氣體，反應結束時各反應物也完全反應完畢。另外，反應物因混合而產生焓的變化因素，在計算中均排除在外，以圖二在常溫常壓的化學反應式為例：$$\mathrm{CO_{(g)}}+\mathrm{NO_{2(g)}}\rightarrow\mathrm{CO_{2(g)}}+\mathrm{NO_{(g)}}$$，其所歷經的過程應該是 $$\mathrm{CO}$$ 和 $$\mathrm{NO_2}$$ 經過 $$(B)$$ 途徑先混合，在經過 $$(C)$$ 發生反應，生成混合在一起的如 $$\mathrm{CO_2}$$ 和 $$\mathrm{NO}$$。最後以人為的方式，經過 $$(D)$$ 途徑再將生成物彼此分開。

事實上，再計算該反應的反應焓時是直接經由 $$(A)$$ 途徑計算，即 $$\mathrm{CO}$$ 和 $$\mathrm{NO_2}$$ 在未混合時的相對焓各為多少，反應完畢後即使有多個產物，也將其視為各別單獨分開，彼此不混合，再分別計算各生成物的相對焓，最後將生成物的所有相對焓減去反應物的所有相對焓，即可得反應焓，亦為該反應方程式的反應熱。一般學子常會認為所計算的反應焓為 $$(C)$$ 途徑，事實上定義的反應焓卻為 $$(A)$$ 途徑者方為正確，二者不同的地方即為 $$(B)$$、$$(D)$$ 兩步驟的混合及分離焓的變化量，由於焓是狀態函數，因此 $$(A)$$ 的反應焓應等於 $$(B)$$、$$(C)$$、$$(D)$$ 三者反應焓的總和。

圖二 標準反應焓的計算為 (A) 步驟的情況，反應物和生成物均各自分開没有混合，和實際進行反應的 (C) 步驟不同。（作者繪製）

三、不同溫度下，標準莫耳反應焓的算法

當反應的溫度不是參考狀態時，例如是 400 K 時，是否也能利用參考狀態的數據，求出相關的數據。首先可以利用表一中給的定壓熱容量，透過下式求出不同溫度下的相對焓：

$$H^{\circ}_{m,400}=H^{\circ}_{m,298}+\int\limits^{400}_{298}C_{p,m,298}dT~~~~~~~~~(7)$$

上式中的定壓熱容量 $$(C_{p,m,298})$$ 若隨溫度改變的量甚小，則在溫度改變不大時，可視為定值，因此上式可改寫成：

$$H^{\circ}_{m,400}=H^{\circ}_{m,298}+C_{p,m,298}\times(400-298.15)~~~~~~~~~(8)$$

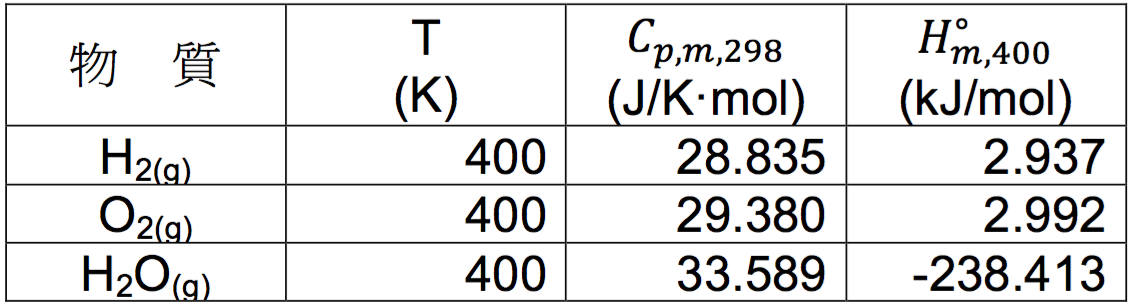
利用 $$(8)$$ 式可將表一的數據換算成表二。

表二 計算在 400 K，1 bar 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據。（作者整理製作）

利用表二可以計算 $$(5)$$ 式在 400 K 的反應焓：

$$\displaystyle\Delta_rH^{\circ}_{m,400}=(-238.413)-(2.937)-\frac{1}{2}\times(2.992)=-242.846~kJ/mol$$

由計算出來的莫耳反應焓或生成焓為 $$-242.846~kJ/mol$$，和表二中的水蒸氣的莫耳相對焓 $$(-238.413~kJ/mol)$$ 不同，其原因即為不在參考狀態時元素的相對焓並不等於 $$0$$。

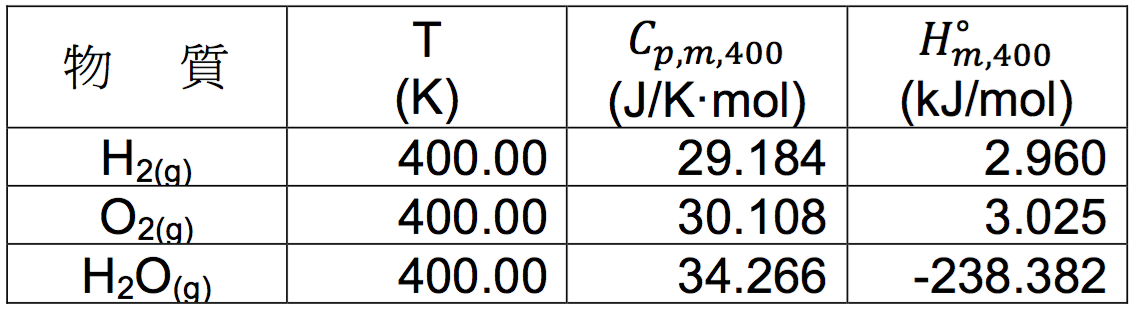
若透過相同網站查表，查詢表二中的各項數據，所得結果如表三，由查表所得出的相關數據和利用表一及（式-8）所得的計算值（表二）相互比較，可看出其相對誤差幾乎可勿略不計。另外，由表二在 298.15 K 時各物種之定壓熱容量和表三在 400 K 時之相對應的熱容量比較，其誤差約為 $$3\%$$，例如水蒸氣在 298.15 K 時為 $$33.589$$，和 400 K 時的 $$34.266$$ 比較，兩者相差不到 $$2\%$$，因此將熱容量視為定值，亦屬合理的範圍。

表三 查表在 400 K，1 bar 下 $$\mathrm{H_2}$$、$$\mathrm{O_2}$$ 及 $$\mathrm{H_2O}$$ 的熱力學數據。（作者整理製作）

連結：反應焓的聯想（三）

參考文獻

1. Levine, I. N. (1988), Physical Chemistry (3rd ed.), McGRAW-HILL Book Company, p211~225.
2. Atkins, P. W. (1994), “Physical Chemistry”, Oxford University Press, Oxford, 5th ed., p. 70~84.
3. 炸彈熱卡計 Bomb Calorimeter｜加百列的部落格。http://blog.udn.com/Gabriel33/5397627
4. Jacobson, N., Journal of Chemical Education, 2001, 78, 814~819.
5. 標準莫耳生成焓與相對熵的求法｜科學Online。/highscope/?p=70277