reaction enthalpy
反應焓的聯想(二)
反應焓的聯想(二)(Thoughts on reaction enthalpy (II))
國立臺灣師範大學化學系兼任教授 邱智宏
連結:反應焓的聯想(一)
現以溫度為 298.15 K 時由氫氣及氧氣生成 $$1$$ 莫耳水蒸氣為例,說明如何求出其標準莫耳反應焓,並藉以釐清反應焓、生成焓及相對焓的異同。
$$\displaystyle\mathrm{H_{2(g)}}+\frac{1}{2}\mathrm{O_{2(g)}}\rightarrow \mathrm{H_2O_{(g)}}~~~~~~~~~(5)$$
一般定義一莫耳純物質若由其成分元素經反應化合而成,則其焓的變化量稱為該物質的莫耳生成焓。
反應焓的聯想(一)
反應焓的聯想(一)(Thoughts on reaction enthalpy (I))
國立臺灣師範大學化學系兼任教授 邱智宏
初學反應焓 (reaction enthalpy) 時經常會產生一些迷惑,首先既然已經有內能 (internal energy, U) 的狀態函數,為何還要增加一個焓 (H) 的狀態函數呢?接著反應熱和反應焓的關係為何?它們是同義詞,還是部分相等,差別在那裏?標準莫耳反應焓 ) 的定義為何?有何重要性?一個物質的莫耳相對焓和莫耳生成焓有何關聯性?最後反應焓除了使用卡計測量以外,有没有其他求法?本文擬以簡單的實例做說明,對上述疑惑做一深入淺出的說明,期盼初學熱力學的學子能有清晰的概念,及紮實的基礎。
標準狀況下理想氣體與真實氣體間的熵值差-以SO2為例(二)
標準狀況下理想氣體與真實氣體間的熵值差-以SO2為例(二)
The entropy difference between the ideal gas and real gas under standard condition – a case study in SO2 (II)
國立臺灣師範大學化學系兼任教師 邱智宏
連結:標準狀況下理想氣體與真實氣體間的熵值差-以SO2為例(一)
二、伯特洛方程式和臨界點
欲求出不同氣態物質在伯特洛方程式中的 $$a$$、$$b$$ 數值,則需對此方程式稍作瞭解。現以水蒸氣為例,以壓力對莫耳體積作圖,在 $$200^\circ C$$ 時,會出現一段水平線(NLJ),即體積減小壓力不變,此時開始有氣體凝結為液體,當溫度愈高時,水平的部分逐漸減短,到 $$374^\circ C$$ 時,水平線成為一點$$(C)$$,此點稱為臨界點( critical point ),此時液、氣間的界面消失,此點的溫度及壓力分別為臨界溫度$$(T_c)$$及臨界壓力$$(p_c)$$。
標準狀況下理想氣體與真實氣體間的熵值差-以SO2為例(一)
標準狀況下理想氣體與真實氣體間的熵值差-以SO2為例(一)
The entropy difference between the ideal gas and real gas under standard condition – a case study in SO2 (I)
國立臺灣師範大學化學系兼任教師 邱智宏
純物質的焓(enthalpy)、自由能(Gibbs free energy)及熵(entropy)是化學熱力學經常要使用到的數據,因此一般化學教科書均會將一些常見物質的相關數據,表列在附錄中,以供參考及使用。但是這些數據是如何求得的?卻鮮少被討論,尤其表列純物質的熵,若在標準狀態下為氣體,則其設定的情況為該氣體為理想氣體。
事實上理想氣體的標準莫耳相對熵$$(S^\circ_{m,id})$$和真實氣體的標準莫耳相對熵$$(S^\circ_{m,re})$$是不一樣的,它們之間的差距是多少?本文擬以 $$\mathrm{SO_2}$$ 為例,利用熱力學的公式,按部就班的推導它們之間的差異,除了讓學子利用所學,真正應用在解決問題上,也期盼學子能感受到在計算過程中數學所扮演的重要角色。
標準狀況下理想氣體與真實氣體間的焓值差-以C2H6為例 (二)
標準狀況下理想氣體與真實氣體間的焓值差-以C2H6為例 (二)
The enthalpy difference between the ideal gas and real gas under standard condition – a case study in C2H6 (II)
國立臺灣師範大學化學系兼任教師 邱智宏
連結:標準狀況下理想氣體與真實氣體間的焓值差-以C2H6為例 (一)
二、伯特洛方程式和臨界點
欲求出不同氣態物質在伯特洛方程式中的 $$a$$、$$b$$ 數值,則需對此方程式稍作瞭解。現以水蒸氣為例,以壓力對莫耳體積作圖,在 $$200^\circ C$$ 時,會出現一段水平線(NLJ),即體積減小壓力不變,此時開始有氣體凝結為液體,
標準狀況下理想氣體與真實氣體間的焓值差-以C2H6為例 (一)
標準狀況下理想氣體與真實氣體間的焓值差-以C2H6為例 (一)
The enthalpy difference between the ideal gas and real gas under standard condition – a case study in C2H6 (I)
國立臺灣師範大學化學系兼任教師 邱智宏
熱力學的主要內容除了三大定律及相關公式外,最常被討論到就是一些狀態函數(state function),而其中經常被使用到的數值,就是純物質的焓(enthalpy)、自由能(Gibbs free energy)及熵(entropy),因此一般化學教科書均會將一些常見物質的相關數據,表列在附錄中,以供參考及使用。
熔點以下的水會自發性結成冰的原因-環境熵和系統熵一樣重要(二)
熔點以下的水會自發性結成冰的原因-環境熵和系統熵一樣重要(二)
The reason of water would spontaneously turn into ice when the temperature is below the melting point – the surrounding entropy is as important as system entropy (II)
國立臺灣師範大學化學系兼任教師 邱智宏
二、不同室溫下,溫度和室溫相等的水會安定存在或轉變成冰
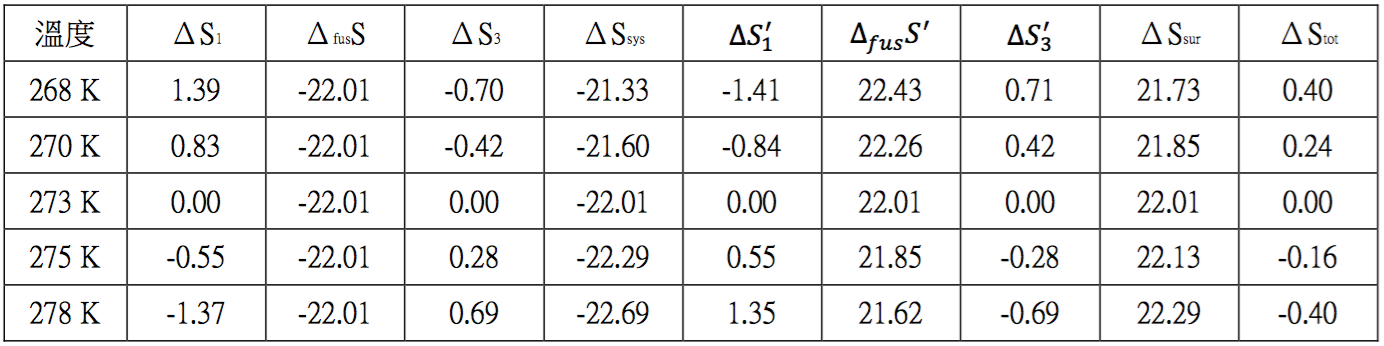
由上面的例題得知,常壓下,室溫為 $$-5^\circ C$$ 時,水會自發性的轉變為 $$-5^\circ C$$ 的冰,如果將室溫提高為$$x^\circ C$$,則 $$x^\circ C$$ 的 $$\mathrm{H_2O}$$ 應該會以水的形式存在?或是以冰的形式存在?我們以上例相同的計算方式,分別計算室溫變為 $$-5$$、$$-3$$、$$0$$、$$2$$、$$5^\circ C$$ 時,各步驟中系統熵和環境熵的變化,其結果詳如表一。
由表一可看出當室溫為 $$270~K(-3^\circ C)$$ 時,其 $$\Delta S_1$$ 相對於 $$268~K$$ 時的 $$1.39$$ 減少,變為 $$0.83$$,即系統由 $$270~K$$ 上升至 $$273~K$$ 時所吸收的熱量,比由 $$268~K$$ 上升至 $$273~K$$ 時來得少的緣故。
熔點以下的水會自發性結成冰的原因-環境熵和系統熵一樣重要(一)
熔點以下的水會自發性結成冰的原因-環境熵和系統熵一樣重要(一)
The reason of water would spontaneously turn into ice when the temperature is below the melting point – the surrounding entropy is as important as system entropy (I)
國立臺灣師範大學化學系兼任教師 邱智宏
熱力學第二定律有許多不同面相的敘述,其中一種說法為:當系統內一個自發性的程序 (spontaneous process) 進行時,系統 (system) 和環境 (surrounding) 中所有熵 (entropy) 變化的總和會大於 $$0$$,即 $$\Delta_{tot}S>0$$(若等於 $$0$$ 則屬以可逆的情況),$$\Delta_{tot} S$$ 等於 $$\Delta_{sur}S+\Delta_{sys}S$$,其中 $$\Delta_{sur}S$$、$$\Delta_{sys}S$$ 分別代表環境熵及系統熵的變化量。
此說法中隱含著三個要素,首先系統的熵大於 $$0$$,並不一定會產生自發反應,小於 $$0$$ 也不一定不會發生,需將環境的熵一併考慮進來,方能判讀。其次自發反應必屬於不可逆 (irreversible) 反應。最後,系統和環境間,熱量的交換,除了正負號不同以外,絕對值應為相等,但是兩者最終的熵卻不相同,可見在系統及環境中一定存在改變它們的條件。
這些要素對於初學物理化學的學子來說略嫌抽象,若能透過日常生活中顯而易見的例子,例如常壓下,$$-5^\circ C$$ 的水,在室溫為 $$-5^\circ C$$ 時會自發性的結成冰,或 $$5^\circ C$$ 的冰在高於熔點的室溫下,會迅速熔化成水,將其變化過程中熵、焓的改變加以計算及說明,或許在思索、領略這些要素時,能獲得事半功倍的效果。