反應焓的聯想（三）
反應焓的聯想（三）(Thoughts on reaction enthalpy (III))
國立臺灣師範大學化學系兼任教授 邱智宏
連結：反應焓的聯想（二）
四、反應焓的求法
圖三 彈卡計示意圖，可以量測易燃元素物質的定容反應熱。（圖片來源：參考資料3）
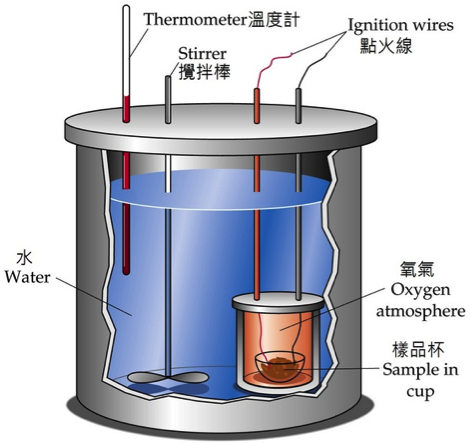
一般化學反應的反應焓或稱反應熱，可由卡計直接由實驗室中測量，例如圖三為常見的彈卡計 (bomb calorimeter)，可以測量在定容下易燃元素的反應熱。定壓下的卡計需將壓力固定，所以會有不同的設計，例如國、高中的酸鹼中和放熱實驗，即為在常壓下藉由保麗龍杯、溫度計，以測量水溫的變化，再換算出反應熱。
除了上述方法以外，若想量測下列反應的反應熱：
$$\mathrm{Ag_2CO_{3(s)}}\rightleftharpoons\mathrm{Ag_2O_{(s)}}+\mathrm{CO_{2(g)}}~~~~~~~~~(9)$$
既無易燃的元素亦非水溶液，很難使用卡計做量測，還好尚有變通的方式，可使用凡特何夫方程式 (van’t Hoff equation) 如下式加以求取。
$$\displaystyle\frac{d\ln K}{d(1/T)}=-\frac{\Delta_r H^{\circ}}{R}~~~~~~~~~(10)$$
其中 $$K$$ 為平衡常數、$$T$$ 為凱氐溫度、$$R$$ 為氣體常數，至於公式 $$(10)$$ 是如何所推導出來？則需勞煩讀者自行參閱物化的教科書。按照 $$(10)$$ 式，只要求出數個不同溫度下的平衡常數，利用 $$\ln K$$ 對 $$1/T$$ 做圖，理論上其圖形為一直線，其斜率即為 $$-(\Delta_rH^{\circ})/R$$，因此反應熱即能求出。以下將此例的詳細步驟做一說明以供參考。首先不同溫度下量測的平衡常數，詳如表四。
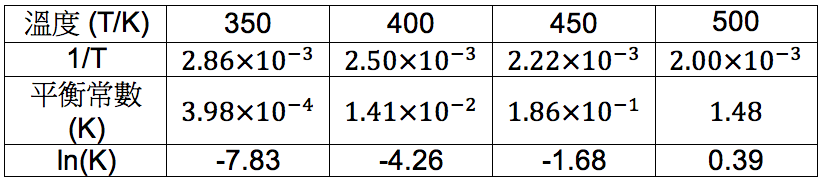
表四 $$\mathrm{Ag_2CO_{3(s)}}\rightleftharpoons\mathrm{Ag_2O_{(s)}}+\mathrm{CO_{2(g)}}$$ 在不同溫度下的平衡常數。（作者整理製作）
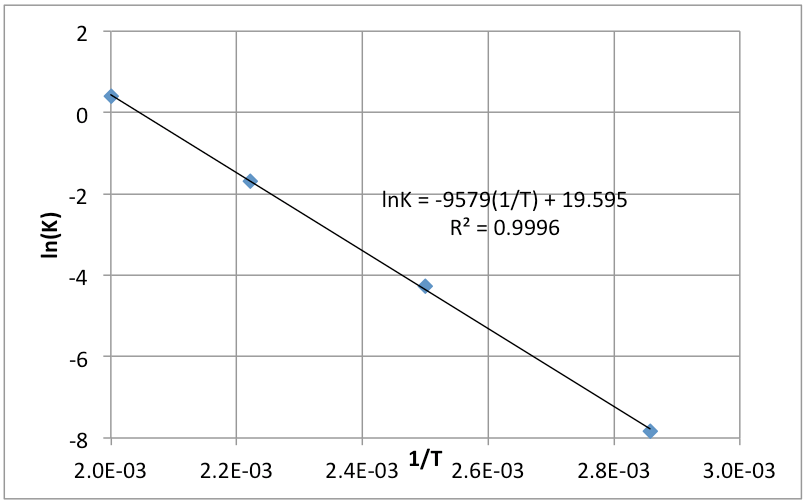
將表四的 $$1/T$$ 為 $$x$$ 軸，$$\ln(K)$$ 為 $$y$$ 軸作圖詳如圖四。圖中 $$4$$ 個實驗數據作線性迴歸，其對應方程式為：$$\ln K = -9579(1/T) + 19.595$$，將其斜率代入式 $$(10)$$，可求出其反應熱為 $$80~kJ/mol$$。
$$\displaystyle -\frac{\Delta_rH^{\circ}}{R}=-9579$$
$$\Delta_rH^{\circ}=-9579\times R=+80~kJ/mol$$
圖四 利用凡特何夫方程式以 $$\ln(K)$$ 對 $$1/T$$ 作圖，求出反應焓。（作者繪製）
上述方法為非卡計求反應焓的方法，其缺點之一為反應焓會隨溫度而改變並非固定值，因此作圖畫出的圖形不一定為直線，但是溫度若僅在很小的範圍區間，或是焓隨溫度的變化量很小時，則此誤差影響不大，在本例中以 $$\ln(K)$$ 對 $$1/T$$ 作圖的結果仍為直線，相關係數非常高為 $$0.999$$。在其他情況下，此法就不見得準確，但卻是經常唯一可使用的方法，因此將求得的數值當成估計值來使用，亦不失為權宜之策。
五、結論
本文利用圖例說明，為何有了內能的狀態函數，仍需要再定義一個焓的狀態函數，主要是因為在定壓下，一個化學反應的反應熱即等於其反應焓，因此在常壓下進行的化學反應，使用 $$\Delta H$$ 比使用 $$\Delta U$$ 來得方便許多。唯反應焓是不是一定要在定壓下測量呢？則不為必然，若在定容而非定壓時系統熱量的變化就不會等於反應焓，反而會等於反應內能的變化。另外，在參考狀態，即 1 bar、298.15 K 時，純物質的標準莫耳生成焓和其標準莫耳相對焓相等，但在不同溫度時兩者便有差異。有了參考狀態後，可以建立一系列物質的標準莫耳生成焓，從事研究者則可利用黑斯定律 (Hess’s Law) 查表計算出大部分反應的反應焓。若要計算非參考狀態溫度的焓則需透過式 $$(7)$$，藉由熱容量即能求出不同溫度下焓的變化量。
一般化學反應的反應焓可由卡計直接測量，唯其條件必須有易燃的元素或容易測量溫度變化的情境，否則不易進行。文中碳酸銀的分解反應便不適合在卡計中進行，但若使用凡何特夫方程式，則可利用不同溫度下的平衡常數，以作圖的方式求得反應焓，屬於一種非卡計的求焓方法。
參考文獻
- Levine, I. N. (1988), Physical Chemistry (3rd ed.), McGRAW-HILL Book Company, p211~225.
- Atkins, P. W. (1994), “Physical Chemistry”, Oxford University Press, Oxford, 5th ed., p. 70~84.
- 炸彈熱卡計 Bomb Calorimeter｜加百列的部落格。http://blog.udn.com/Gabriel33/5397627
- Jacobson, N., Journal of Chemical Education, 2001, 78, 814~819.
- 標準莫耳生成焓與相對熵的求法｜科學Online。/highscope/?p=70277
前一篇文章
下一篇文章
