反應焓的聯想（一）

反應焓的聯想（一）(Thoughts on reaction enthalpy (I))
國立臺灣師範大學化學系兼任教授 邱智宏

初學反應焓 (reaction enthalpy) 時經常會產生一些迷惑，首先既然已經有內能 (internal energy, U) 的狀態函數，為何還要增加一個焓 (H) 的狀態函數呢？接著反應熱和反應焓的關係為何？它們是同義詞，還是部分相等，差別在那裏？標準莫耳反應焓 ) 的定義為何？有何重要性？一個物質的莫耳相對焓和莫耳生成焓有何關聯性？最後反應焓除了使用卡計測量以外，有没有其他求法？本文擬以簡單的實例做說明，對上述疑惑做一深入淺出的說明，期盼初學熱力學的學子能有清晰的概念，及紮實的基礎。

一、反應熱和焓及內能的關係

依熱力學的定義，內能的變化量 $$(dU)$$ 可由下式表示：

$$dU=dq+dw=dq-pdV~~~~~~~~~(1)$$

即一個系統的內能變化量或一個化學反應系統的內能變化量，若除了膨脹壓縮的功 (work) 以外，没有其他形式的功，如電功、表面張力功等，則其大小等於系統熱量的改變量 $$(dq)$$ 加上做功的改變量 $$(dw)$$，當系統吸熱時，$$dq$$ 為正值，放熱時則為負值。系統對外做功時，需要耗掉系統的能量，故為負值，外界對系統做功時則為正值，其大小可以 表示（或 $$dw = -pdV$$)，上式等號右邊有負號的原因為：當系統被壓縮時（即外界對系統做功），由於 $$V_2<V_1$$，$$pdV$$ 積分後為負值，再乘上負號所以 $$dw$$ 為正值，與定義相符。既然內能變化量可以估算熱量的變化，為何還需要另一個焓的狀態函數呢？

圖一 系統由外界吸收熱量 $$(q)$$ 並且對外做功，則其內能變化會比所吸收的熱量小。（作者繪製）

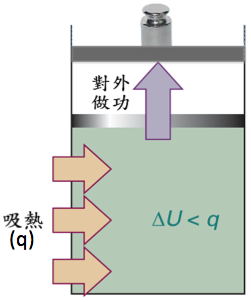
試想在一個「等壓」的狀況如圖一所示，當系統從環境 (surrounding) 吸熱 $$q$$，若此時系統的體積也同時向外膨脹，相當於系統對外做功。由於功也是能量的一種，因此系統吸進熱量所增加的內能，有一部分必須用來對外做功，最終造成系統內能的增加量 $$(\Delta U)$$ 小於吸進的熱量 $$(q)$$。由上所述可知，在等壓的情況下，系統熱量的變化無法由內能的變化量單獨表示出來，恰恰一般化學反應大多在等壓下進行，因此若在此情況下，有一個函數可以直接表示反應熱量的變化，則有其方便性，焓的定義於焉產生如下：

$$H=U+pV~~~~~~~~~(2)$$

當系統的焓，因吸熱或放熱而產生變化時上式可表示為：$$dH=d(U+pV)=dU+pdV+Vdp=dq-pdV+pdV+Vdp$$
上式已將 $$dU$$ 以 $$(1)$$ 式代入，另外由於等壓的關係 $$dp=0$$，因此上式可表示為

$$dH=dq_p~~~~~~~~~(3)$$

由於在等壓的條件下，系統熱量的變化（$$dq_p$$、等壓下的熱量變化）就等於焓的變化量，因此等壓下一個化學反應熱量的變化，一般稱為反應熱，也就等於反應焓，此時二者為同義詞。但是如果反應不是在等壓下進行時，則二者並不相等，例如在等容下進行，則熱量的變化可直接由 $$(1)$$ 式求得，由於 $$dV=0$$ 所以 $$dw$$ 也等於 $$0$$，因此

$$dU=dq_V~~~~~~~~~(4)$$

二、標準狀態的定義及參考狀態的選擇

一般教科書或網站上列表的熱力學數據，均有其訂定的標準狀態 (standard state)，通常其狀態為 1 bar 下的某特定溫度，若此溫度為 25℃，則以 $$H^{\circ}_{m,298}$$ 表示在 298.15 K 的標準莫耳相對焓，其中上標 o 表示標準壓力為 1 bar，下標的 $$m$$ 表示單位莫耳，另外，若純物質為氣態，則假定在標準狀態其為理想氣體，而非真實氣體。

由熱力學定律雖可以計算出純物質焓的變化量，卻無法得知其絶對的焓，因此必需了解學術界如何定義相對焓。首先必需選擇在某特定參考狀態 (reference state) 下，所有在最穩定狀態的元素，其相對焓均為 $$0$$，再測量出由特定狀態到欲求狀態的焓值變化量。

對於焓而言，選擇 1 bar、298.15 K 是最方便的參考狀態，即對所有元素在其最穩定的狀態時規定其$$H^{\circ}_{m,298}=0$$。有多種同素形體時，則以最常見或最重要的同素異形體訂為 $$0$$，例如碳、硫、磷、氧的異形體中則分別以石墨、斜方硫、白磷（黃磷）、O₂ 的元素訂為 $$0$$。將各種不同的元素的標準相對焓均隨意設為 0，並不會造成計算上的錯誤，因為化學反應進行時，不同元素間並不會互相轉換。有了元素的相對焓以後，化合物在參改狀態的相對焓要如何求得？最方便的方法就是在等壓下直接測量由其組成元素生成該化合物時的熱量變化。

連結：反應焓的聯想（二）

參考文獻

1. Levine, I. N. (1988), Physical Chemistry (3rd ed.), McGRAW-HILL Book Company, p211~225.
2. Atkins, P. W. (1994), “Physical Chemistry”, Oxford University Press, Oxford, 5th ed., p. 70~84.
3. 炸彈熱卡計 Bomb Calorimeter｜加百列的部落格。http://blog.udn.com/Gabriel33/5397627
4. Jacobson, N., Journal of Chemical Education, 2001, 78, 814~819.
5. 標準莫耳生成焓與相對熵的求法｜科學Online。/highscope/?p=70277