利用Gnuplot軟體繪製似氫原子的徑向分佈函數（上）
利用Gnuplot軟體繪製似氫原子的徑向分佈函數（上）(Hydrogen-like radial distribution Plots Using Gnuplot (I))
國立臺灣師範大學化學系兼任教授 邱智宏
學習原子軌域時，經常產生一個疑惑，即電子出現密度最大的地方，卻不是最容易找到電子的區域？教科書中常以 $$4\pi r^2\times|\psi^2|$$ 對原子半徑 $$(r)$$ 作圖來做解釋，卻不是直接以波函數 $$(\phi)$$ 或電子出現機率密度 $$(\psi^2)$$ 對 $$r$$ 作圖，為何還要乘上 $$4\pi r^2$$ 呢？ 究其不了解的原因，主要是數學式子太過抽象，教科書的圖形又無法親自繪製，很難從中領略其中的神髓。
在網路上頗為盛行的免費繪圖軟圖：gnuplot，由於具有可跨平台、輕薄短小、易於操作及功能強大等優點，已廣泛的被使用在各個學科領域中。筆者曾撰寫一篇其應用在量子化學上的文章：《利用 Gnuplot 軟體繪製似氫原子的軌域形狀》，目前放在高瞻平台上以供參考，主要是利用 gnuplot 軟體繪製原子軌域的立體形狀，本文則將其應用導向平面圖形的繪製，探討如何利用此軟體的各項指令，繪製出原子半徑對各類波函數分佈的具體圖形。另外，也利用 gnuplot 具有程式語言的功能，示範如何用數值解的方式，計算出軌域在不同區間中，電子出現的機密究竟有多大。讀者在閱讀本文時，可一邊按照文中的指示操作電腦，相信從做中學，會有事半功倍之效。
一、似氫原子 $$s$$ 軌域的波函數隨原子半徑變化的分佈圖
由薛丁格方程式 (Schrödinger equation) 解出的似氫原子 (hydrohen-like atom) $$1s$$、$$2s$$、$$3s$$ 的波函數分別如下：
$$\varphi_{1s}=\displaystyle\frac{1}{\sqrt{\pi}}(\frac{Z}{a_0})^{\frac{3}{2}}e^{-Zr/a_0}$$ （式-1）
$$\varphi_{2s}=\displaystyle\frac{1}{4\sqrt{2\pi}}(\frac{Z}{a_0})^{\frac{3}{2}}\left(2-\frac{Zr}{a_0}\right)e^{-Zr/2a_0}$$ （式-2）
$$\varphi_{3s}=\displaystyle\frac{1}{81\sqrt{3\pi}}(\frac{Z}{a_0})^{\frac{3}{2}}\left(27-18\frac{Zr}{a_0}+2\frac{Z^2r^2}{a^2_0}\right)e^{-Zr/3a_0}$$ （式-3）
其中 $$a_0$$ 為波耳半徑等於 $$0.53$$Å，$$Z$$ 為原子核的正電數，對於氫原子而言 $$Z=1$$，另外作圖時以 $$r/a_0$$ 作為座標尺度，因此在撰寫指令集時 $$Z$$ 和 $$a_0$$ 均可省略不寫。將波函數的值對原子半徑作圖，若利用 gnuplot 做圖，其指令集詳如圖一，大部分的指令已在前一篇文章中說明，讀者可自行參考，但為了方便了解及查詢，仍在圖一中加註說明，其中只要有「#」符號出現，該行從這個位置以後的文字均為說明或註解，並不會執行。
圖一、gnuplot 指令集，藉以繪出氫原子 $$1s$$、$$2s$$ 及 $$3s$$ 軌域波函數隨原子半徑改變的分佈圖（圖片來源：作者製作）
圖一中有關波函數的設定部分，即依據（式-1）、（式-2）、（式-3）所設定，最後二行指令由於太長，所以使用倒斜線 $$(\backslash)$$ 連接，程式會自動將其解讀為同一行。而 plot Phi1s(x) lw 2 lc “red” title “1s”，代表畫 (plot) 第一個波函數 (Phi1s(x))，線寬（lw、line width的縮寫）為 2 號，線的顏色（lc、line color的縮寫）使用紅色，圖例標籤為 ”1s”，其他接續的二條線也是用相同的指令，只是改變波函數和顏色。這裏尚須提醒一下，畫平面圖形時使用 plot 指令，畫立體圖形時則必須使用 splot。
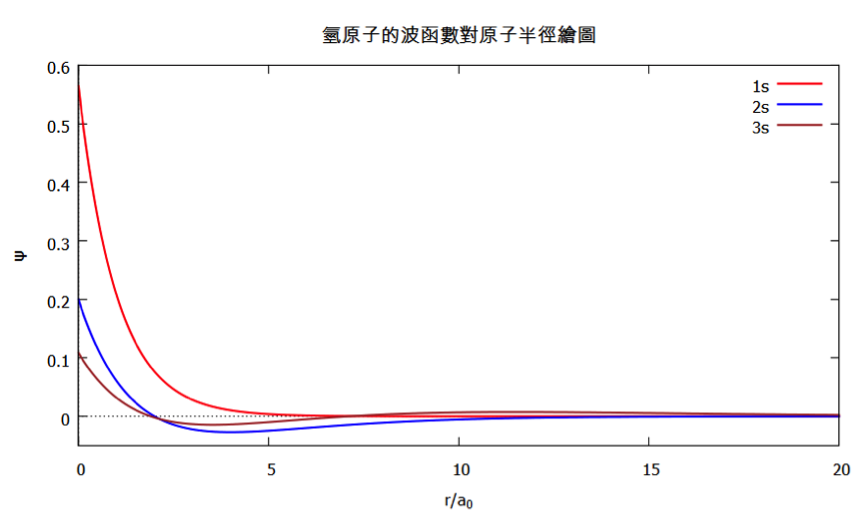
將圖一的指令集以文字檔存入喜歡的檔名，開啟 gnuplot 程式，在游標處輸入下列指令：load “檔名.txt”，即可畫出圖形詳如圖二，其中 x 座標的刻度為 $$r/a_0$$，由圖中可看出 $$1s$$ 波函數的值，在 $$r=0$$ 時最大，隨著 $$r$$ 值的增大遞減的很快，其值均為正。而 $$2s$$ 波函數雖然也是在 $$r=0$$ 最大，但其隨著 $$r$$ 值遞減的速度較 $$1s$$ 慢，並在某一個特殊的位置其波函數的值為零，代表此處電子出現的機率為 $$0$$，由上列 $$2s$$ 的波函數可知，即圖二的藍色線在 $$r$$ 不是無限大時，（式-2）的指數部分不可能為 $$0$$，因此唯有 $$(2-\frac{Zr}{a_0})=0$$ 時，波函數才有可能為 $$0$$，因此 $$r=\frac{2a_0}{Z}$$ 時即為節點出現的位置，節點以前函數值為正，節點以後其值為負。$$3s$$ 波函數（圖中的棕色線）則出現 $$2$$ 個節點，讀者可從（式-3）中求出，其函數值從第一個節點由正變負後，在第二個節點以後再由負變為正。
圖二、利用 gnuplot 繪製氫原子 $$s$$ 軌域的波函數隨原子半徑改變的分佈圖（圖片來源：作者繪製）
二、機率密度及徑向分佈函數的區別
由量子化學的結論可知，電子在空間中某點出現的機率密度 (probability density)，正比於波函數在該處的平方值，因此我們可以利用 gnuplot 將電子機率密度隨原子半徑改變的分佈情形繪製出來，首先僅需將圖一中的最後二行，修改為 plot Phi1s(x)**2 lw 2 lc “red” title “1s” , Phi2s(x)**2 lw 2 lc “blue” title “2s” , Phi3s(x)**2 lw 2 lc “brown” title “3s”，順便將 y 軸的標題改為 ，即將 set ylabel “”改為 set ylabel “^2”，在 gnuplot 的語法中，^、_ 分別代表下一個字母以上、下標顯示，當然標題也改過了，讀者可以自行練習。修改過的指令集，經執行後可得圖三的圖形。
圖三、利用 gnuplot 繪製氫原子 $$s$$ 軌域電子的機率密度隨原子半徑改變的分佈圖（圖片來源：作者繪製）
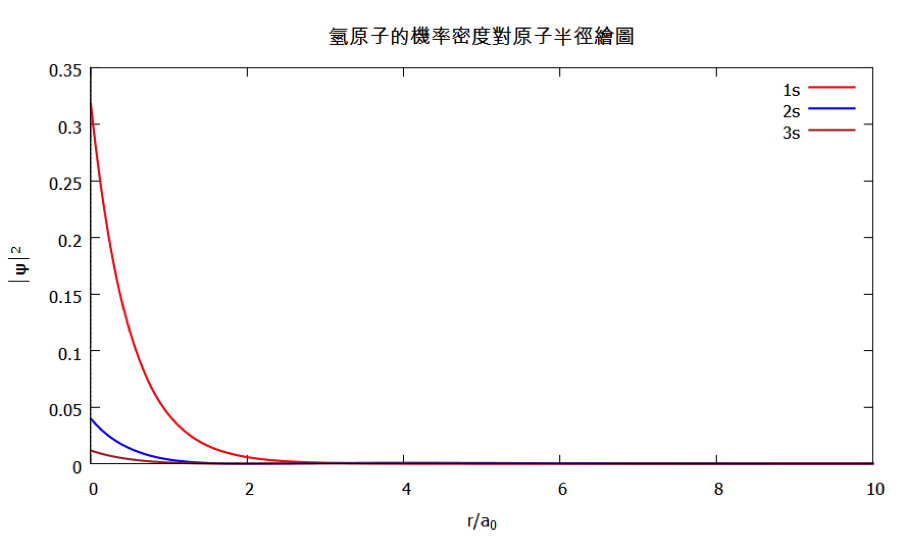
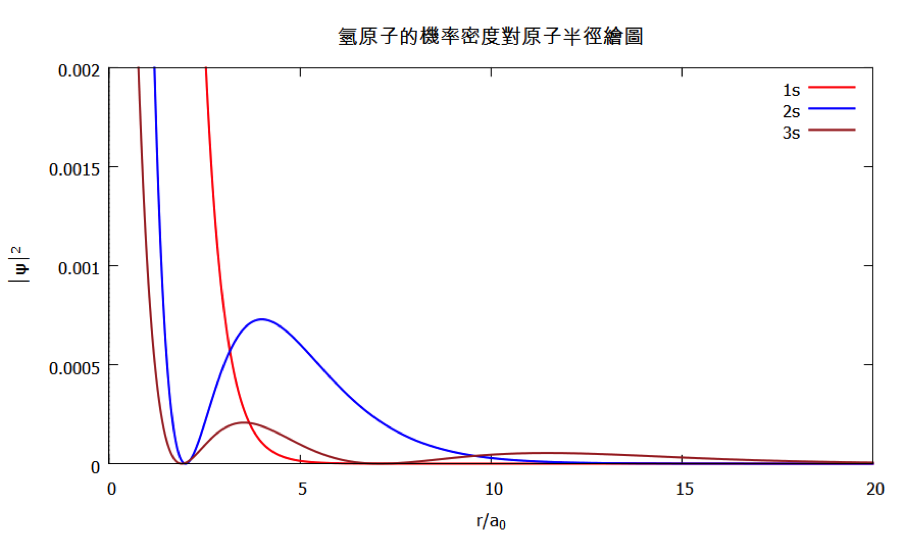
由圖三可看出，電子機率密度出現最高的地方均為原子核所在的位置，即 $$r=0$$，隨著 $$r$$ 值的增大快速遞減。在這裏有二個疑問產生，首先電子出現機率最大的地方和一般認知不同，不是出現在距離原子核特定距離的地方嗎？其次圖三並没有出現節點？第二個疑問主要來自節點出現的位置，大約 $$r$$ 等於 $$2$$ 及 $$7$$ 的附近，其機率密度太低，以至於被線圖掩蓋著，因此只要重新設定 y 軸的範圍，將 set ylabel [0.,0.002] 加入圖一中的文字檔中，其出現的位置只要在 plot 指令之前皆可，重新執行後即可得圖四。由圖四中確實可看出，$$2s$$ 有一個節點，而 $$3s$$ 有二個節點。
圖四、將圖三的 y 軸範圍設定為 $$0$$ 至 $$0.002$$ 之間，以觀察圖形的細部變化（圖片來源：作者繪製）
連結：利用Gnuplot軟體繪製似氫原子的徑向分佈函數（下）
參考文獻
- gnuplot homepage. http://gnuplot.info/
- 地圖/統計圖/3d 函數圖/實驗報告圖 — Gnuplot 純畫圖｜”資訊人權貴” 之家。 http://user.frdm.info/ckhung/b/ma/gnuplot.php
- gnuplotスクリプトの解説｜米澤進吾 ホームページ http://www.ss.scphys.kyoto-u.ac.jp/person/yonezawa/contents/program/gnuplot/index.html
- 马欢 (2012)。使用 gnuplot 科学作图｜Gnuplot 中文教程。 http://www.phy.fju.edu.tw/files/archive/876_ab57aed9.pdf
- N. Levine (2008), Physical Chemistry (6th ed.). McGRAW-HILL Book Company. p637~647.
- Spherical Polar Coordinates – HyperPhysics. http://hyperphysics.phy-astr.gsu.edu/hbase/sphc.html
- 葉名倉、劉如熹、邱智宏、周芳妃、陳建華、陳偉民（2013 年）高級中學化學選修上冊。南一書局。第14～26頁。
- Saputra, A., Canaval, L. R., Fadiawati, N., Diawati, C., Setyorini, M., Kadaritna, N., & Kadaryanto, B. (2015). Visualizing Three-Dimensional Hybrid Atomic Orbitals Using Winplot: An Application for Student Self Instruction. Journal of Chemical Education, 92(9), 1557-1558.
- Chung, W. C. (2013). Three-dimensional atomic orbital plots in the classroom using Winplot. Journal of Chemical Education, 90(8), 1090-1092.
- Moore, B. G. (2000). Orbital Plots Using Gnuplot. Journal of Chemical Education, 77, 785-789.
前一篇文章
下一篇文章
