利用Gnuplot軟體繪製似氫原子軌域的等高線圖（下）(Using Gnuplot plot the contour map of hydrogen-like orbital (II))
國立臺灣師範大學化學系兼任教授 邱智宏
連結：利用Gnuplot軟體繪製似氫原子軌域的等高線圖（上）
圖四、利用 gnuplot 軟體繪製 $$3p_x$$ 軌域波函數的形狀及其等高線圖（作者繪製）
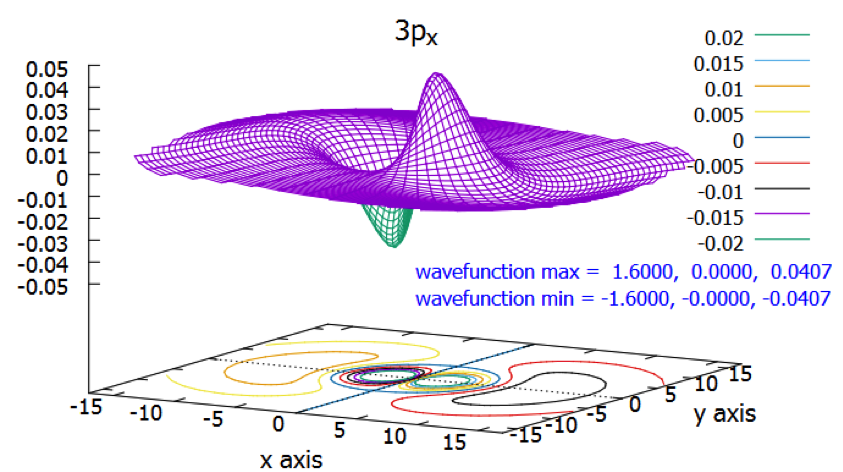
圖四中 $$z$$ 軸即為 $$3p_x$$ 波函數的值，由圖中可看出其值有正亦有負，正值代表在 $$xy$$ 平面上方有凸起的部分，有一個山峰及一個較平緩的小山丘，凹下去的部分為負值，有一個深的山谷及一平緩的小山溝。
利用Gnuplot軟體繪製似氫原子軌域的等高線圖（上）(Using Gnuplot plot the contour map of hydrogen-like orbital (I))
國立臺灣師範大學化學系兼任教授 邱智宏
學習原子軌域時，經常由於太過抽象，常使學習者敬而遠之，因此一般教科書均會各種圖形加以輔助說明，例如原子軌域的3D形狀、徑向分佈函數(radial distribution function)對原子半徑的變化圖及波函數的電子出現機率之等高線圖(contour map)等，但是學子仍然無法理解，這些圖形是如何繪製出來的？倘若有一個適宜的繪圖軟圖工具，讓學子親自繪製及感受各類軌域間的特徵及變化，相信對於學習效果會有事半功倍的效果。
利用Gnuplot軟體繪製似氫原子的徑向分佈函數（下）(Hydrogen-like radial distribution Plots Using Gnuplot (II))
國立臺灣師範大學化學系兼任教授 邱智宏
連結：利用Gnuplot軟體繪製似氫原子的徑向分佈函數（上）
接下來，探究第一個疑問，一般會出現這樣的矛盾，主要是將機率密度和徑向分佈函數 (radial distribution function) 弄混，前者是空間某一特定點電子出現的機率密度，而密度要乘上體積才是距原子核某特定距離電子出現機率的大小。
利用Gnuplot軟體繪製似氫原子的徑向分佈函數（上）(Hydrogen-like radial distribution Plots Using Gnuplot (I))
國立臺灣師範大學化學系兼任教授 邱智宏
學習原子軌域時，經常產生一個疑惑，即電子出現密度最大的地方，卻不是最容易找到電子的區域？教科書中常以 $$4\pi r^2\times|\psi^2|$$ 對原子半徑 $$(r)$$ 作圖來做解釋，卻不是直接以波函數 $$(\phi)$$ 或電子出現機率密度 $$(\psi^2)$$ 對 $$r$$ 作圖，為何還要乘上 $$4\pi r^2$$ 呢？ 究其不了解的原因，主要是數學式子太過抽象，教科書的圖形又無法親自繪製，很難從中領略其中的神髓。
利用 Gnuplot 軟體繪製似氫原子的軌域形狀（下）(Hydrogen-like orbital plots using gnuplot (II))
國立臺灣師範大學化學系兼任教授 邱智宏
連結：利用 Gnuplot 軟體繪製似氫原子的軌域形狀（上）
圖三的文字檔以 fourier.txt 存檔後，可在 gnuplot 視窗的游標列上輸入：load “fourier.txt”，讓 gnuplot 讀取檔案後，一次執行一系列的指令以完成任務，當然讀取檔案的路徑必須正確，若不正確則無法順利執行。當內定路徑無法找到檔案時，可利用視窗中 ChDir 的下拉式選項改變讀取檔案的路徑。
利用 Gnuplot 軟體繪製似氫原子的軌域形狀（上）(Hydrogen-like orbital plots using gnuplot (I))
國立臺灣師範大學化學系兼任教授 邱智宏
高中或大學化學課程，每當遇到物理化學領域時，原子軌域、波函數 (wave function)、機率密度 (probability density) 等，對一般學子而言就一個抽象了得！連課本中軌域的形狀是怎樣畫出來的也是丈二金剛，摸不著頭腦，既使知道怎麼畫出來的，也找不到適當的軟體，親自體驗一下。專業軟體如 maple、 mathematic 不是太貴，就是太複雜，簡易軟體如 excel，又不符需求，因此這一單元的教材，由於缺乏具體的圖像及做中學的體驗，往往是學子學得較不理想的部分。
基態氫原子之最可能半徑及平均半徑的比較（下）(The comparison between the most probable radius and the average radius of hydrogen ground state (II))
國立臺灣師範大學化學系兼任教授 邱智宏
二、最可能半徑、平均半徑及原子軌域範圍的求法
欲求電子出現機最大的地方，則需對徑向分佈函數微分後，令其等於 $$0$$ 求極值即可：
$$\displaystyle\frac{\partial[r^2R(r)^2]}{\partial r}=\frac{\partial[r^2(\frac{Z}{a_0})^3e^{-\frac{2Zr}{a_0}}]}{\partial r}=(2r-2\frac{Z}{a_0}r^2)(\frac{Z}{a_0})^3e^{-\frac{2Zr}{a_0}}=0$$
$$r=a_0/Z=a_0=0.53$$ Å
比較2p及3p氫原子軌域的等高線圖（下）
Comparing the contour map of hydrogen atom’s 2p and 3p orbitals (III)
國立臺灣師範大學化學系兼任教授 邱智宏教授
比較2p及3p氫原子軌域的等高線圖（中）
Comparing the contour map of hydrogen atom’s 2p and 3p orbitals (II)
國立臺灣師範大學化學系兼任教授 邱智宏教授
二、$$\varphi_{2p_z}$$ 及 $$\varphi_{3p_z}$$ 軌域等高線圖的畫法
圖二、三的軌域形狀雖然能告訴我們很多訊息，但是其內部的電子分部情形，究竟是均勻分佈？還是遂漸變大或變小？卻無法表示出來。另外有一種常用的表達方式稱為等高線圖，恰能補其不足。想像一下，如何在二度空間，表示一座高山的地形圖？