三角函數圖形的平移與伸縮
三角函數圖形的平移與伸縮
臺北市立西松高中 蘇惠玉教師
在將角度轉換成弧度之後,對於實數 \(x\),我們都可以將其考慮成弧度,進一步定義它的某個三角函數值。例如正弦函數,對每一個實數 \(x\),定義 \(f(x)=\sin x\)。定義完六個三角函數之後,可以利用描點的方式繪出函數圖形。
例如 \(y=f(x)=\sin x\) 的圖形如下: 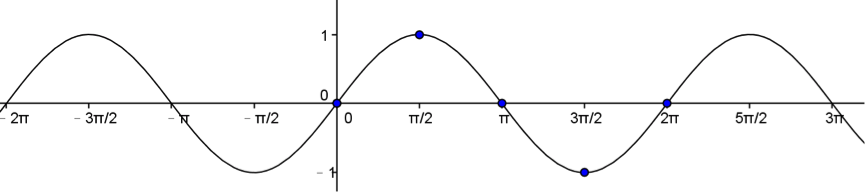 接下來,筆者將以 \(f(x)=\sin x\) 的圖形為例,來說明三角函數圖形的平移與伸縮如何作圖,
接下來,筆者將以 \(f(x)=\sin x\) 的圖形為例,來說明三角函數圖形的平移與伸縮如何作圖,
以及平移與伸縮對圖形的基本特徵如週期、振幅與極值的影響。
圖形的平移
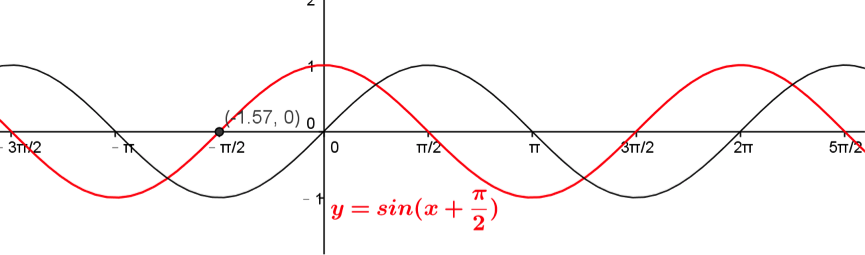
首先,考慮 \(y=\sin{(x+\frac{\pi}{2})}\) 與圖形 \(y=\sin x\) 的關係。
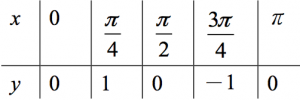
因為 \(x\) 方向有變動,因此可考慮對應 \(y\) 值為 \(0,1,0,-1,0\) 這幾個點的 \(x\) 值,如下表:
描點繪出圖形如下圖中紅色之曲線,
可以看出其與 \(y=\sin x\) 圖形的關係,為 \(y=\sin x\) 圖形向左平移 \(\frac{\pi}{2}\)。
從上圖中也可看出紅色的曲線 \(y=\sin{(x+\frac{\pi}{2})}\) 的圖形,與 \(y=\cos x\) 的圖形可完全重合,
因此可知 \(y=\sin x\) 的圖形往左移 \(\frac{\pi}{2}\),即可得到 \(y=\cos x\) 的圖形。
由正弦與餘弦的關係亦可得到它們圖形的這個特性,因為 \(\sin{(x+\frac{\pi}{2})}=\cos x\)。
從這個例子推廣,考慮 \(y=\sin{(x-c)}\) 與圖形 \(y=\sin x\) 的關係,
以 \(y=\sin x\) 圖形為基礎,\(c>0\) 時,圖形往右移 \(c\) 單位;當 \(c<0\) 時,圖形往左移 \(c\) 單位。
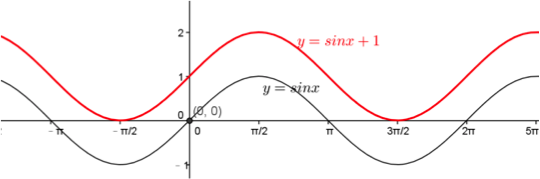
接著是 \(y\) 方向的平移,考慮 \(y=\sin x+1\) 與 \(y=\sin x\) 兩圖形的關係。
先利用描點繪出 \(y=\sin x +1\) 的圖形:
繪出圖形如上右圖中紅色之曲線,
可以看出其與 \(y=\sin x\) 圖形的關係,為 \(y=\sin x\) 圖形向上平移 \(1\) 單位,
此時函數的極大值為變為 \(2\),極小值為 \(0\)。
從這個例子推廣,考慮 \(y=\sin x+d\) 與圖形 \(y=\sin x\) 的關係,
以圖形 \(y=\sin x\) 為基礎,\(d>0\) 時,圖形往上移 \(d\) 單位;
當 \(d<0\) 時,圖形往下移 \(d\) 單位,此時函數的極值會產生變化。
圖形的伸縮
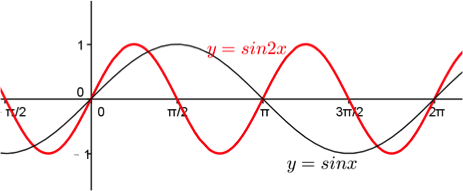
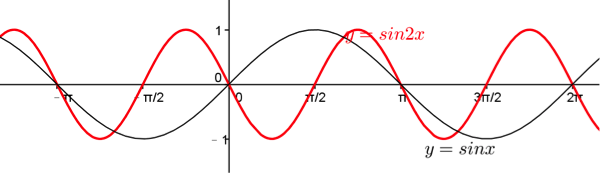
考慮 \(y=\sin{2x}\) 與 \(y=\sin x\) 圖形的關係。
因為 \(x\) 方向有變動,因此可考慮對應 \(y\) 值為 \(0,1,0,-1,0\) 這幾個點的 \(x\) 值,如下表:
描點繪出圖形如上右圖中紅色之曲線,可以看出與 \(y=\sin x\) 圖形的關係,
其圖形為 \(y=\sin x\) 圖形以原點為伸縮中心,\(x\) 方向伸縮 \(\frac{1}{2}\) 倍(\(x’=\frac{1}{2}x\))。
因此原本 \(y=\sin x\) 圖形的週期為 \(2\pi\),經過壓縮,可得 \(y=\sin{2x}\) 圖形的週期為 \(\frac{2\pi}{2}=\pi\)。
從這個例子推廣,考慮當 \(b>0\) 時, \(y=\sin(bx)\) 與 \(y=\sin x\) 圖形的關係,
以 \(y=\sin x\) 圖形為基礎,原點為伸縮中心,作 \(x\) 方向的伸縮,其週期變為 \(\frac{2\pi}{b}\)。
當 \(b<0\) 時,只須再考慮對 \(x\) 軸作對稱即可,
以 \(y=\sin{(-2x)}=-\sin{2x}\) 為例,其圖形如下:
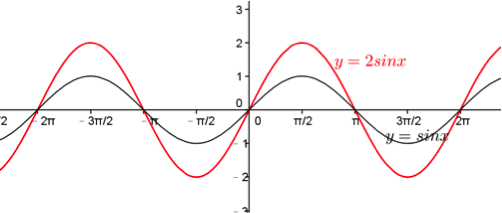
接著是 \(y\) 方向的伸縮。考慮考慮 \(y=2\sin x\) 與 \(y=\sin x\) 兩圖形的關係。
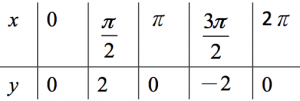
先利用描點繪出 \(y=2\sin x\) 的圖形:
繪出圖形如上右圖中紅色之曲線,可以看出其與 \(y=\sin x\) 圖形的關係,
為 \(y=\sin x\) 圖形以原點為伸縮中心,\(y\) 方向伸縮 \(2\) 倍(\(y’=2y\))。
因此原本 \(y=\sin x\) 圖形的振幅為 \(1\),經過伸縮,可得 \(y=2\sin x\) 圖形的振幅 \(1\times 2=2\)。
從這個例子推廣,考慮當 \(a>0\) 時,\(y=a\sin x\) 與 \(y=\sin x\) 圖形的關係,
以 \(y=\sin x\) 圖形為基礎,原點為伸縮中心,作 \(y\) 方向的伸縮,其振幅變為 \(a\)。當 \(a<0\) 時,
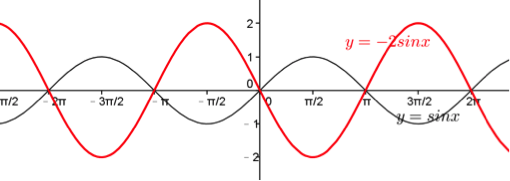
只須再考慮對 \(x\) 軸作對稱即可,以 \(y=-2\sin x\) 為例,其圖形如下:
當 \(x\) 方向的平移與伸縮同時進行時,要特別注意其平移量的多寡。
例如 \(y=\sin{(2x-\frac{\pi}{2})}\) 的圖形,考慮原本 \(y=\sin x\) 圖形中之 \((0,0)\) 這個點的變化,
當 \(2x-\frac{\pi}{2}=0\) 時,\(y=0\),此時 \(2x=\frac{\pi}{2},x=\frac{\pi}{4}\),
亦即 \(y=\sin{(2x-\frac{\pi}{2})}\) 為 \(y=\sin x\) 的圖形右移 \(\frac{\pi}{4}\) 後再作 \(x\) 方向伸縮 \(\frac{1}{2}\) 倍。
也就是說,要將 \(y=\sin{(2x-\frac{\pi}{2})}\) 化成 \(y=\sin{(2(x-\frac{\pi}{4}))}\) 來考慮。
綜合論之,考慮 \(y=a\sin{[b(x-c)]}+d\) 圖形與 \(y=\sin x\) 圖形的關係,
在原本的 \(y=\sin x\) 圖形中,振幅變為 \(|a|\) 倍;週期變為 \(\frac{2\pi}{|b|}\);
當 \(c>0\) 時,往右移 \(c\) 單位,當 \(c<0\) 時,往左移 \(c\) 單位;
當 \(d>0\) 時,往上移 \(d\) 單位,當 \(d<0\) 時,往下移 \(d\) 單位,此時函數的極值會產生變化。


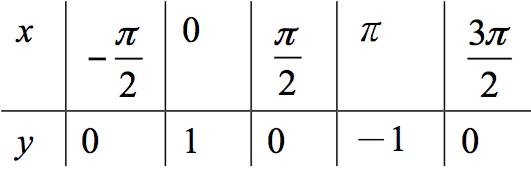
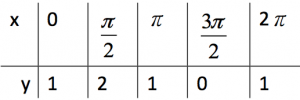
 前一篇文章
前一篇文章 下一篇文章
下一篇文章

我想問一下,正弦、餘弦…..等三角函數的名稱是如何定義的?或是說,正弦是正那一條弦?有人可以幫忙解釋嗎?謝謝