彈性力 Elastic Force
彈性力 Elastic Force
國立臺灣大學物理研究所張翔恩
在介紹彈性力之前,我們先來說說甚麼是彈性(elasticity)。如果一個物體受到應力的作用而使其變形,過了一段時間,應力消失了,而該物體又恢復成原來的形狀,我們就稱該物體具有彈性。而讓該物體恢復原有形狀所需要的恢復力,就是彈性力。一般而言,當形變不是很大時,彈性力是遵守線性定律的,也就是說彈性力的大小會和造成物體形變的大小成比例關係(如圖一)。
彈性力 Elastic Force
國立臺灣大學物理研究所張翔恩
在介紹彈性力之前,我們先來說說甚麼是彈性(elasticity)。如果一個物體受到應力的作用而使其變形,過了一段時間,應力消失了,而該物體又恢復成原來的形狀,我們就稱該物體具有彈性。而讓該物體恢復原有形狀所需要的恢復力,就是彈性力。一般而言,當形變不是很大時,彈性力是遵守線性定律的,也就是說彈性力的大小會和造成物體形變的大小成比例關係(如圖一)。
傅科擺(Foucault pendulum)
國立臺灣大學物理所黃一玄
「這現象靜默的展現,既無形也永不停止。人們可以感覺到,可以看到它穩定的生成,它不受人為力量而加快或是減緩。看到這件事實的任何人都會駐足沉思、沉默片刻。而之後伴他離去的,則是那個對我們在太空中持續不間的運行有更敏銳體驗的永恆感覺。」
───傅科 (譯自Amir D. Aczel, Pendulum : Léon Foucault and the Triumph of Science, p xi, Atria Books (2004))
非慣性座標系 (Non-Inertial Reference Frame)
國立臺灣大學物理所黃一玄
若某一座標系相對於任一慣性座標系有加速度,則該座標系稱之為非慣性座標系。在非慣性座標系中,物理定律並非處在最簡單形式,特殊地,對於一個質量為 、受到外力為 $$F$$ 的質點來說,牛頓定律不再能單純地寫成 $$F=ma’$$ 的形式(其中 $$a’$$ 是非慣性座標系的觀察者所測到質點的加速度)。為了方便描述物體的運動,人們遂引入假想力的概念,令 F+F假想力 =ma’ ,使牛頓定律的形式得以成立。
雖然我們永遠可以選擇只採用慣性座標系來描述物體的運動,然而這並不總是處理問題最合適的方式。例如我們如果想了解受壓力梯度影響下的大氣移動,則因為我們是跟著地球在自轉,為了能非常直接而方便地應用到日常生活中,我們會選擇將計算的結果以隨著地球自轉的這個非慣性座標系來表示。
拉密定理 (Lami’s Theorem)
國立臺灣大學物理系陳昱璟
拉密定理 (Lami’s theorem)是靜力學中的一個定理,用於靜力學系統與機械系統的分析。此定理是由法國數學家Bernard Lami (1640-1715;Lami亦有拼成Lamy者)所提出。在力學中,我們常常利用向量來分析系統的運動狀態,而拉密定理最常用來解決三力平衡之問題,可以省去分解向量後的繁複計算,但對於超過三個作用力之問題,其便利性便大幅下降。其公式內容及證明如下:
公式:若三力 ($$F_A$$、$$F_B$$、$$F_C$$) 作用於一物體上,其合力為零 ($$\vec{F_B}+\vec{F_B}+\vec{F_C}=\vec{0}$$) ,並共點,則任一力的量值與其他兩力夾角之正弦值的比值皆相等。
$$\displaystyle \frac{F_A}{\sin \alpha}=\frac{F_B}{\sin\beta}=\frac{F_C}{\sin\gamma}$$
正向力 (Normal Force)
國立臺灣大學物理系蘇冠禎
正向力怎麼來的?
當物體放在一個平面上時,這個平面會因形變而產生一個推向此物體的力,因為這個力垂直平面,所以被稱為正向力(normal force),normal在此就是「垂直」的意思。
想像一下,你站在一個墊子上,這個墊子會向下產生形變而給予你一個向上的正向力,此力與你身體的重力抵消,使你不會掉下去。在真實世界裡「剛體(rigid body)」並不存在,也就是說,每個物體都能夠產生形變,所以即使你是站在堅硬地板上,地板一樣會形變而提供正向力,只不過它形變的程度非常微小罷了。
正向力有多大?
想像在一個電梯裡,你站在體重機上面,體重機數值顯示的就是機器內部彈簧形變的程度,我們將此數值稱為「視重」。此時你受到兩個力,一個是地球給你的重力向下,另一個是體重機給你的正向力向上。
虎克定律 Hooke’s law
中央大學物理所余韋德
在介紹虎克定律(Hooke’s law)之前,先來回想一下當初學習牛頓第二定律時,我們知道當一個物體所受的外力和不為零時,該物體會產生加速度的運動,但物體受力除了會產生加速度造成運動狀態改變之外,另外該物體亦可能會產生外型的改變,故力的效應可以造成物體運動狀態改變和形變,若對形變現象有興趣想深入了解,那虎克定律可作為進入研究形變的第一個功課。
基本上虎克定律是在描述:當固體材料受力之後,材料中的應力與變形量(應變)之間成線性關係。也就是一個固體的受力和它的變形量(應變)是成正比的意思。而彈簧即是日常生活中常見且符合虎克定律的範例,故將以彈簧來為大家進行虎克定律的介紹。當你施力去拉長或是壓縮一條彈簧時,該彈簧便會伸長或是變短,產生簡單的一維形變。在這條彈簧的彈性限度內,你施力的大小將會影響到這條彈簧的形變程度,虎克定律應用在彈簧上即描述彈力與彈簧變形量的關係。
等加速運動 (Uniformly Accelerated Motion)
國立臺灣大學物理系簡嘉泓
等加速運動為物理學上的運動型態之一,等加速運動有兩個特性:運動軌跡為直線、加速度為定值。我們知道加速度為一向量,向量相等的條件為方向及大小都相同,所以等加速度運動亦即加速度之方向與大小皆不隨時間改變之運動。
公式推導
由加速度為定值這項特性,我們可以推導出等加速度運動的幾項基本公式:由 $$a-t$$ (加速度-時間)圖(如圖一)可得速度的變化量 $$\Delta v=at$$ ─ 式 $$(1)$$,而以 $$v_0$$ 為初始速度,$$v_f$$ 為最終速度,可得 $$v_0+\Delta v=v_f$$ ─ 式 $$(2)$$。
功率(Power)
國立臺灣大學物理系陳昱璟
簡介
功率(Power)是能量轉換或是使用的速率,以單位時間所消耗的能量大小來表示。國際標準制(SI)的單位為瓦特(Watt),用來紀念蒸汽引擎的設計人十八世紀英國著名發明家詹姆斯‧瓦特(James Watt)。瓦特數越高代表單位時間所消耗的能量越高。
單位
除了國際標準制的功率單位瓦特($$W$$)等於一焦耳每秒其他功率單位還包括:爾格每秒($$erg/s$$),等於 $$10^{-7}$$ 瓦特;馬力($$hp$$),也就是一分鐘將 $$550$$ 磅的重物提高一英尺所需的功率,約等於 $$746$$ 瓦特;分貝毫瓦($$dBm$$),這是以一毫瓦為基準的對數值;此外還有卡每小時(或是千卡每小時)、英熱單位每小時($$Btu/h$$)、以及冷凍噸,而一冷凍頓約等於 $$3,517~kW$$,常用在冷氣或空調系統。
人造衛星 (Satellite)
台中縣縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理系洪連輝教授責任編輯
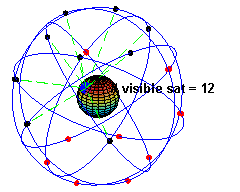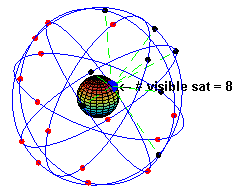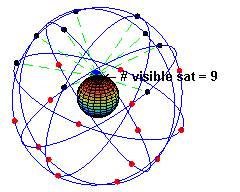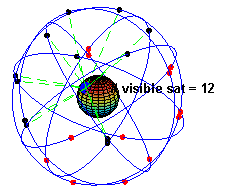 所謂人造衛星是指人類製造的載具,經由火箭或太空梭發射到外太空,不斷繞行地球運轉的衛星。
所謂人造衛星是指人類製造的載具,經由火箭或太空梭發射到外太空,不斷繞行地球運轉的衛星。
人造衛星依照軌道運行的種類可以分為同步 (Geo-stationary orbit) 與極軸 (Polar orbit) 衛星。所謂同步衛星指的是在赤道上空約 36000 公里,繞行地球週期與地球自轉週期相同的衛星,因為與地球同步,故稱為同步衛星,也因為同步,因此在地球上觀察此類衛星有如靜止於空中,因此又稱為地球靜止軌道衛星。至於極軸衛星,則是軌道面垂直於地球的赤道面,因為軌道面垂直於赤道面,所以 訊號可以分布到全球各地,例如現在的全球定位系統(Global Position System,簡稱為 GPS)就是利用二十四顆的極軸衛星,組成衛星網,提供通訊的服務。
加速度(Acceleration)
台中縣縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理系洪連輝教授責任編輯
所謂加速度是運動學上的一個量,它與位置(position)、速度(velocity)同為運動學三大基本量。加速度是速度對時間微分,加速度對時間積分就會是速度變化。
加速度也可以是動力學的量,它代表力(force)與質量(mass)的比值,不過這樣的表示方式,只是一種簡化的表示方式,只有在質量維持不變情形才會成立,當質量隨時間改變時,牛頓第二定律就必須修正為力是動量對時間微分,而非力等於質量乘以加速度。