潤德勒弔詭 (Rindler Paradox)
國立臺灣大學醫學系100級 林欣妤
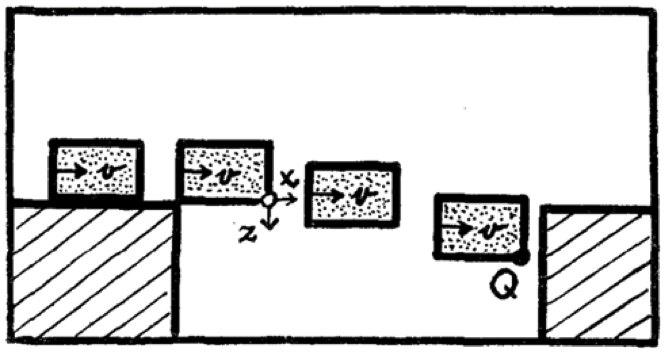
為了澄清狹義相對論中關於長度測量以及同時性之概念，潤德勒(Wolfgang Rindler)在1961年提出此一弔詭，又稱「棒子與洞的弔詭」(rod and hole paradox)。狹義相對論告訴我們，觀測一個以接近光速移動的物體時，會發現它的長度變短了 (為原本的 \(\sqrt{1-\frac{v^2}{c^2}}\) 倍) ！
假設有個棒狀的剛體在桌上高速前進，遇到一個和它靜止時長度相同的洞，那棒子是否會掉進洞裡呢？現在有兩位觀察者，\(A\) 相對靜止於桌面，而 \(B\) 跟著棒子高速移動。對 \(A\) 來說棒子高速接近桌上的洞，由相對論我們知道，他會認為棒子的長度變短，在飛過洞的一小段時間中棒子下落了一點，最終掉進洞裡(Fig. 1)。
Fig.1 由 \(A\) 的觀點，長度縮短的棒子受重力影響下墜到洞中
穀倉-竿弔詭 (Barn-pole paradox)
國立臺灣大學物理系100級 潘孝儒
穀倉-竿弔詭是狹義相對論中著名的弔詭之一，問題的敘述是這樣子的，有位農夫擁有一座穀倉和一根竿子，但是竿子太長以至於無法放進穀倉中，於是聰明的農夫突然想到，在狹義相對論中，高速移動的物體長度會縮短，所以只要將竿子加速到夠快的速度便可以讓竿子完整放入穀倉中一段時間(因為竿子在運動，所以只能期望它會在穀倉中待一小段時間)。這看似很合理，不過從竿子的慣性座標系來看，穀倉以高速向自己移動，所以穀倉將會比原本的長度更小，所以竿子根本不可能放入穀倉中！所以問題到底出在哪裡呢？究竟哪個觀察者的結論才是正確的？
事實上，兩個觀察者的結論都是正確的！你可能會問，這樣沒有矛盾嗎？怎麼可能竿子同時在裡面又在外面？問題的癥結點在於，對於兩個不同慣性座標系的觀察者而言，這些事並不是同時發生的。
原子鐘 (Atomic clock) 發展背景與現況及高精度時鐘在基礎科學扮演的角色
東京大學理學博士黃郁珊編譯/國立臺灣大學科學教育發展中心陳藹然博士責任編輯
自古以來時間的計時依賴的是規律而週期的變化，比如說每天的日升日落。後來人類發明了機械式的鐘擺時鐘，其準度可達10-5。而較晚發明的石英振盪器所產生的電子振盪訊號可到達10-9的穩定度，使之成為原子鐘發明前最精準的計時方式。由於傳統的鐘擺或是電子振盪器的頻率易受環境條件的強烈影響（例如溫度、濕度、材質老化等等），使得他們的計時精確度無法得到進一步的突破。相對地，原子內部能階的躍遷頻率 (transition frequency) 基本上取決於各種基本常數因而具有極小的環境影響參數。因此，原子的內部躍遷頻率成為極有價值的計時參考源。自1950年以來原子鐘就成為世界上最準的計時儀器。
目前世界上最精準的時鐘－光晶格光頻原子鐘在低溫環境下的突破
東京大學理學博士黃郁珊編譯/國立臺灣大學科學教育發展中心陳藹然博士責任編輯
編譯來源：次世代時間標準「光格子時計」の高精度化に成功（科学技術振興機構(JST) 2月10日新聞稿）
東京大學香取秀俊教授的研究團隊在2015年二月份的《自然光子學期刊》 (Nature Photonics) 發表他們的光晶格光頻原子鐘的研究成果，該研究團隊成功地打造兩台以鍶原子為基礎的最先進光頻原子鐘（如圖一），藉由兩台原子鐘的互相比較，證明其相對誤差在2×10-18的範圍內，相當於兩台時鐘須花160億年才會產生１秒的相對誤差。此外，透過系統分析，這兩台原子鐘的不準確度(inaccuracy)為7.2×10-18，這是世界上首次的成果，相較於目前用來定義「秒」的微波銫原子鐘，其準確度高了一百倍。
為什麼保溫瓶要抽真空？ (How vacuum helps thermos do their job)
國立臺灣大學物理系二年級101級 曾奕晴
保溫杯的主要功能，顧名思義，就是將瓶中的承裝物體維持在一定的溫度，也就是盡量避免保溫瓶中的物體和外界產生熱平衡的熱量交換現象。
雙原子氣體的比熱 (Specific heat of diatomic gases)
國立臺灣大學物理系101級 鍾豪
能量均分原理（equipartition principle）是指：「若某分子具有 $$f$$ 種儲存能量的方式，則該分子在溫度為 $$T$$ 時所具有的平均能量為 $$f\times \frac{1}{2}k_BT$$，其中 $$k_B$$ 為波茲曼常數(Boltzmann constant)。」在此，「均分」代表每一種儲存能量的方式互相獨立，且皆帶有 $$\frac{1}{2}k_BT$$ 的平均能量。也因為每一種方式之間互相獨立，所以 $$f$$ 種方式又稱 $$f$$ 個「自由度」。
