化學 | 科學Online

催化劑

2011/12/22

催化劑 (Catalyst)
國立臺灣大學化學系學士生陳佳翰/國立臺灣大學化學系陳藹然博士責任編輯

催化劑(Catalyst)又稱觸媒，是一種以改變反應途徑的方式來影響反應活化能，藉以增快或減慢化學反應，但反應前後卻質量不變的物質。例如：某催化劑A能降低反應活化能30 kJ/mol，則根據阿瑞尼亞士方程計算，在體溫37℃(310 K)下，反應速率約增快113540倍。

催化劑可分為三大類：
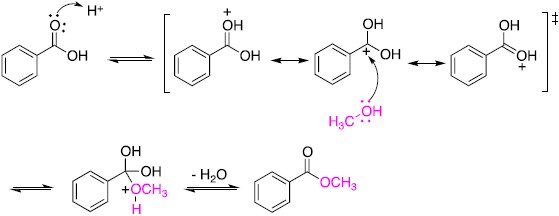
1. 均相觸媒或勻相觸媒(homogeneous catalyst)。此類催化劑與反應系統同一相態如液相或氣相，觸媒和反應物能均勻混合，因此在催化過程中並沒有受到觸媒與反應物接觸表面積大小的限制。常見的酸催化酯化反應(acid-catalyzed esterification)即為在有機酸溶液中添加些許硫酸作為催化劑，使得羧酸基團(C(=O)(OH))上C=O的氧原子被質子(H⁺)活化形成活化錯合體(activated complex)，醇的氧原子攻擊此活化錯合體中帶部份正電的碳原子，得到反應中間體(intermediate)，最後脫去一分子水得到酯類(圖一)。

圖一、酸催化酯化反應的反應機構(reaction mechanism)。

繼續閱讀→

湮滅(Annihilation)

2011/11/23

尚無留言

湮滅(Annihilation)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

湮滅(Annihilation)，字面上意指物質的消滅，是當一個粒子(particle)與其相對應的反粒子(antiparticle)互相碰撞之後，物質粒子轉變為高能光子(photon)型式的電磁波，例如電子(electron)與正子(positron)的湮滅（式一）、以及質子 (proton)與反質子(anti-proton)的湮滅：
e + e⁺ → γ + γ （式一）

由於該粒子與反粒子兩者的量子態彼此相反，當兩者碰撞後物質粒子雖然消失，但不是什麼都沒有了，由於能量守恆以及動量(momentum)守恆、角動量(angular momentum)守恆等物理定律，粒子湮滅還是有存留下來的東西，那就是能量。根據愛因斯坦的能量守恆定律(E = mc²)0.5克物質湮滅所產生的能量約100萬千卡，相當於廣島原爆釋出的能量。

低能量的湮滅，所產生的粒子為光子，光子為無質量之粒子，如上述之電子與正電子的湮滅。這是因為電子所擁有的質量能量(mass-energy)太低，不具產生較重新物質粒子之條件。此外由於粒子本身的靜止能(rest energy)不夠高，因此只足夠產生兩個或是多個的γ射線光子；因為在電子與正電子碰撞湮滅的瞬間，兩者為靜止，系統動量為0，必須有兩個相反方向的光子產生才能維持動量守恆。

繼續閱讀→

陰極保蝕

2011/11/23

尚無留言

陰極保蝕 (Cathodic Protection)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

陰極保蝕(cathodic protection)，是利用電化學原理，在一個電化學系統當中，陽極的金屬會氧化，而成為金屬離子溶入電解質溶液當中；而陰極則會產生還原反應，使得在溶液當中的一些金屬離子，或者是能夠被還原的物質在陰極上面還原。由於陰極的金屬在此情況下，並不會溶解到溶液當中，換言之保護位於陰極金屬不被侵蝕。

繼續閱讀→

β粒子

2011/11/23

有 1 則留言

$$\beta$$ 粒子(Beta Particles)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

$$\beta$$ 粒子(beta particles)指具有高能量、高速的電子或正子(positron)。當放射性核種進行 $$\beta$$ 衰變(beta decay)時，除了產生衰變後的原子之外，還會同時高能粒子，這些高能粒子因而被命名為 $$\beta$$ 粒子。而由於 $$\beta$$ 衰變又分為 $$\beta^+$$ 與 $$\beta^-$$ 衰變，分別產生正子與電子，因此正子與電子又分別被稱作為 $$\beta^+$$ 與 $$\beta^-$$ 粒子。

繼續閱讀→

化學氣相沉積法(Chemical Vapor Deposition)

2011/11/22

尚無留言

化學氣相沉積法(Chemical Vapor Deposition)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

化學氣相沉積法，是一種化學上常用的合成過程，其目標是生產高效能且高純度的一些化學材料。例如像是人工鑽石的合成，以及半導體業上的薄膜合成，都是透過化學氣相沉積法來達到。而化學氣相沉積法製造鑽石的發現，有效地提升了鑽石的產量與應用性。

一個典型的化學氣相沉積法，是將我們所使用的基底(substrate)，暴露於欲合成之材料的前驅物蒸氣當中，常見的基底如矽、金屬或金屬化合物；當前驅物蒸氣接觸到基底，便可能會發生不同的變化，譬如沉積、分解等反應產生欲合成附著在基底上，當這些分子持續累積，便會得到我們所想要的材料。

例如像是在半導體產業上，我們將晶圓作為基底，暴露在不同的蒸氣下，可以得到矽、二氧化矽、氮化矽(Si₃N₄)，甚至是一些金屬的薄膜沉積。

我們使用矽烷蒸氣可以得到矽：

SiH₄ → Si + 2 H₂

繼續閱讀→

比爾定律(Beer’s Law)的限制

2011/11/18

尚無留言

比爾定律(Beer’s Law)的限制
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

比爾定律，又稱作比爾──朗伯定律(Beer-Lambert Law)，是一個光學基礎定律。當光穿透樣品溶液時，光的吸收度(A)與吸收係數( )、光徑長(l)、濃度(c) 三者均呈正比：A=lc

然而，比爾定律並不適用各種狀況，只適用在某些前提與限制下：
1. 溶液必須是一個均質的溶液，不能存在不均勻的現象。
2. 溶液當中的分子彼此之間不互相作用，例如稀薄溶液。
3. 溶質分子不會因入射光的照射而進行反應。
4. 溶液必須是澄清的，也就是說不能產生散射現象。
5. 僅考慮光的吸收，忽略光的散射、反射等行為。
6. 光源使用單色的平行光。也就是每一束光是相同的波長，且通過相同長度的介質溶液，因為莫耳吸收係數會隨著波長而有所不同。

當測量條件不符合上述前提，以比爾定律計算出的結果就會出現大幅誤差。例如由於濃度的增加，而造成溶液當中組成成分的改變，使得吸光係數並非恆定。例如在水中鉻酸根離子與二鉻酸根離子遵守下列的平衡反應：

繼續閱讀→

比爾定律與吸收度

2011/11/18

有 3 則留言

比爾定律 (Beer’s Law)與吸收度 (Absorbance)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

比爾定律，又稱作比爾──朗伯定律(Beer-Lambert Law)，是一個光學基礎定律。當光穿透樣品溶液時，光的吸收度 $(A)$ 與吸收係數 $(\alpha)$、光徑長 $(l)$、濃度 $(c)$ 三者均呈正比：$A=\alpha lc$

其中 $\alpha$ 為吸收係數(absorptivity，或稱 absorption coefficient)，亦可稱為消光係數(extinction coefficient, $k$)。然而，若是在光徑長 $b$ 使用了 cm 作為單位，並且濃度 $c$ 使用 $M$ 作為單位，吸收係數以 $M^{-1}cm^{-1}$ 作為單位，那麼這時候的吸收係數，即可稱為莫耳吸收係數(molar absorptivity)，其符號以 $\varepsilon$ 來代表。莫耳吸收係數 $\varepsilon$ 的使用相當頻繁，以至於還比吸收係數 $\alpha$ 來的常出現。因此，常見的比爾定律表示方法為：$A=\varepsilon bc$

此外，我們需要瞭解的另一個重要定義是光的吸收度(absorbance)。當一束光線照射到一樣品溶液時，部份的光線會被樣品溶液吸收，剩下的光線則穿透樣品溶液，即原本光入射線強度 $I_0$，穿透光線強度變為 $I_1$，此時光的穿透度 $T$ (Transmittance)，即光穿透的比例為

圖一、比爾定律吸收光路徑的示意圖。(圖片來源： WIKIPEDIA–Beer–Lambert law)

繼續閱讀→

比爾定律的應用

2011/11/18

有 1 則留言

比爾定律(Beer’s Law)的應用
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

比爾定律的應用，通常是針對已知莫耳吸收係數的溶液，透過測量光吸收度推算出溶液濃度。這種透過光學方法測量濃度的方法包含了比色法 (colorimetry)、光電比色法(photoelectric colorimetry)、分光光度法(spectrophotometry)等。

繼續閱讀→

能斯特方程式

2011/11/15

有 6 則留言

能斯特方程式 (Nernst equation)
國立臺灣大學化學工程系碩士生吳宗澤/國立臺灣大學化學系陳藹然博士責任編輯

能斯特方程式(Nernst equation)，由德國的化學家瓦爾特.赫爾曼.能斯特 (Walther Hermann Nernst, 1864 – 1941) 所提出，描述電化電池 (Electrochemical cell) 的化學反應中電動勢 (Electromotive force, emf) 與反應物濃度商數 (Reaction quotient) 的方程式；用來決定電化電池中半電池反應(Half-cell)的平衡還原電位 (Equilibrium reduction potential)，或計算電化電池的電動勢。能斯特方程式廣泛應用於計算非標準態下的電動勢，例如，生物細胞膜內外的電位差，用於解釋神經系統的運作。

繼續閱讀→