等效電阻

等效電阻 (Equivalent Resistance)
國立臺灣大學物理學系 劉仁宇

在提及等效電阻前先來複習一下甚麼是電阻，電阻一般是符合歐姆定律 $$\frac{V}{I}=$$ 常數的電子元件，例如鎳鉻絲，因此我們令電阻 $$R=\frac{V}{I}$$ 為一隨溫度變化之常數。此外電阻還跟材料特性、形狀有關，如高中所學過的 $$R=\rho\frac{lL}{A}$$，其中 $$\rho$$ 為與物質和溫度相關之常數、L, A 分別為該物質長度和面積。

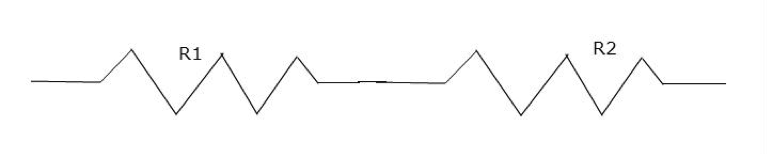
等效電阻就是說如果有很多個電阻出現在電路中，我們可以將它視為一個電阻，這就稱作等效電阻。首先我們先來看看串聯，見圖一，串聯的特性是流經兩個電路元件的電流是一樣的，因為電阻不能有電荷積聚，若電流為 I、兩電阻的電壓分別為 V₁, V₂，此時我們將兩個電阻想成一個等效電阻，為了確認是否可以這樣做，等一下你/妳可以檢查該等效電阻是否為一常數，$$R=\frac{V}{I}=\frac{V_1+V_2}{I}=R_1+R_2=$$ 常數，所以我們可以得知串聯的等效電阻為兩電阻值直接相加。

圖一、電阻串聯。（本文作者劉仁宇繪）

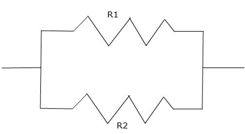
接下來我們來看看並聯吧，如圖二，並連的特性是兩端的電壓都是一樣的（因為兩個元件電壓不相等會造成其中一端電位不相等而矛盾），設它為 V 如同先前的作法，假設流經二電路元件電流分別為 I₁, I₂，等效電阻 $$R=\frac{V}{I}=\frac{V}{I_1+I_2}=(R^{-1}_1+R^{-2}_2)^{-1}=$$ 常數，可以得知並連的等效電阻為兩電阻倒數和的倒數而且也是一個定值。以上的串聯和並聯都可以推廣到任意數量的電阻，用的也是一樣的規則，又或者你 / 妳可以試試兩兩不斷合併的歸納法，物理意義就是把兩個電阻當作一個等效電阻再和其他電阻當作等效電阻…。

圖二、電阻並聯。（本文作者劉仁宇繪）

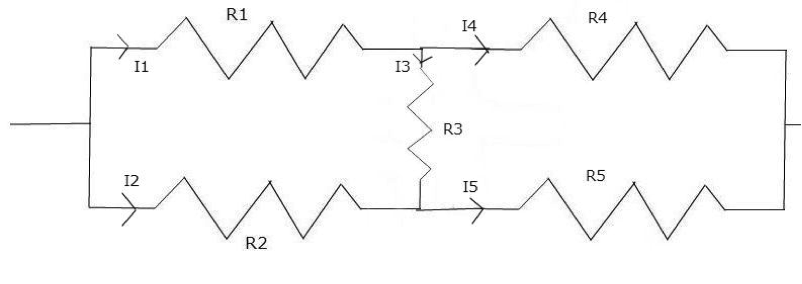
然而有些電路不是串聯也不是並聯怎麼辦呢，如圖三。這個找不到可以分拆的部分，那我們只好回歸最原始的方法：假設流經各個電阻的電流並解出我們要的等效電阻 $$R=\frac{V}{I}$$，條件有 $$I=I_1+I_2=I_4+I_5$$，$$I_3+I_4=I_1$$，而關於電壓我們採用克西荷夫的迴路定律，也就是順著任意路徑繞一圈後電位差為零，所以有 $$V=I_1R_1+I_4R_4=I_2R_2+I_5R_5$$ 和 $$I_2R_2=I_1R_1+I_3R_3$$，現在我們有五個未知數和四條方程式，稍微計算一下可以發現其中四個未知數都可以用另外一個變數來表示。例如我們若用 I₁ 當作該獨立變數，如此一來 I 可以表示成 I₁ 乘以某個常數，V 也可以表示成 I₁ 乘以某個常數，所以等效電阻 R 也是一個常數，所以這個電路是有等效電阻的，因為過於複雜，通常會採程式解或是將電路實際以三用電表測試，如果不得已必須手算，可以邊解邊帶入 R₁ 等數值可以大幅降低複雜程度。

圖三、橋式電路。（本文作者劉仁宇繪）

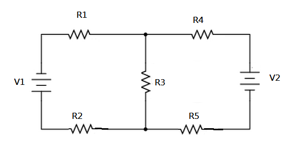
同樣的方法可以用在各式各樣的複雜電路，如圖四，依據克西荷夫的節點和迴路定律可以解出等效電阻，針對僅由電阻組成的電路都會有等效電阻，這是因為歐姆定律的特性，然而加上了其他電路元件如二極體、電容、電感等就不是這麼一回事了，因為他們不遵守歐姆定律，如果在直流電路直接帶等效電阻的算法 $$R=\frac{V}{I}$$ 會得到 R 隨時間而改變，並不是一個定值，在此等效電阻的觀念就不適用。有趣的是，有一個觀念叫作阻抗，在交流電路中使用，概念和電阻一樣，只是讓它變成複數帶有電流和電壓存在相位差的概念，阻抗的公式如下 $$Z=\frac{V}{I}$$，如此一來電容、電感等元件在交流電路的阻抗是一個定值，就可以用等效阻抗的方式來處理，有興趣的讀者可以參考科學Online網站上《RC 電路》和《RL 電路》這兩篇文章。

圖四、複雜的電路。（本文作者劉仁宇繪）

事實上，圖三的電路稱作橋式電路，在電路學中可以轉換成比較簡單串聯加並聯電路，因為牽涉到較複雜的理論在此暫且不談。至於等效電阻有甚麼功用呢，當遇到的電路過於複雜可以把它一部分一部分簡化掉，最後變成一目了然的簡單電路，甚至只剩下一個等效電阻。現在你是不是覺得輕鬆多了呢？

參考文獻

1. Sedra, A. S., & Smith, K. C. (2009), Microelectronic Circuits, Oxford University Press.
2. Nilsson, J. W., & Riedel, S. (2007), Electric Circuits, Prentice Hall.