滲流（下）

Posted on 2016/05/10 in 物理, 統計物理 Statistical Physics, 臨界現象 Critical Phenomena with 尚無留言 1,532 views

滲流（下） (Percolation (II))
西北大學物理與天文學系博士生林蔚廷、西北大學物理與天文學系博士生楊暘

當我們在考慮地下水流動時，我們把地層當作一堆整齊排列的方格（稱之為晶格）來處理。這雖然是很粗糙的想法，但晶格模型確實抓住了「隙縫是連接地層中相近的兩個點」這個物理上的重點。換句話說，空間中距離很遠的兩個點，比如說地表及地下深處，是不應該有管道直接連接的。因此描述地層，晶格還算是說得通的。

然而並非所有介質總是像土壤這樣固定不變。在流行病研究中，傳播的介質是人。很顯然的，用晶格來描述社會結構或人際關係，是一定行不通的。那麼我們該如何研究這類的系統呢？

在流行病爆發的研究中，除了複雜的人際關係網路之外，疾病的傳染力，人體的免疫反應等等，許多因素都有影響。在此我們一樣討論一個最簡單的模型，看看是否一樣有相變這樣有趣的現象。

我們假設社會中的每個人都由一個點來代表，兩個人之間可以互相傳染疾病的話，就用一條線將兩個點連起來。這條線之於病原，就如同隙縫之於地下水一樣，是可流通的路徑。決定是否能傳染是非常複雜的，最簡單的模型，就是如同之前一樣，假設對任意兩個人，有機率 $$p$$ 是會互相傳染的（路徑存在），機率 $$(1-p)$$ 是不會傳染的（路徑不存在）。

假設我們有一個由 $$n$$ 個人組成的人際關係網路。其中，平均每個人可以傳染（或者被傳染）的人數則是 $$c=np$$。對任意一個人，我們定義 $$u$$ 為他沒有處於網路中最大的傳染通路中的機率。那麼，我們可以用一個自洽方程來計算 $$u$$：

$$u=(1-p+pu)^{n-1}$$

這個等式可以這樣理解：對於某一個人甲，不屬於最大通路的機率（等式左邊）應該等於他沒有和任何一個在最大通路上的人相聯通的機率（等式右邊）。這個機率可以這樣計算：對於網路中其他 $$n-1$$ 個人，只能是沒有與某甲相連（機率為 $$1-p$$），或者是相連但是自身不在最大通路中（機率為 $$pu$$）。用 $$p=\frac{c}{n}$$ 來代換並對兩邊取對數，這個方程式進一步可以寫為：

$$\ln(n)=\displaystyle (n-1)\ln(1-\frac{c}{n}+\frac{c}{n}u)$$

當網路裡有很多人 ($$n\gg 1$$) 的時候，通常會有 $$\frac{c}{n}\ll 1$$，我們進一步可以使用近似 $$n-1\approx n$$ 和近似 $$\ln(1-x)\approx -x$$

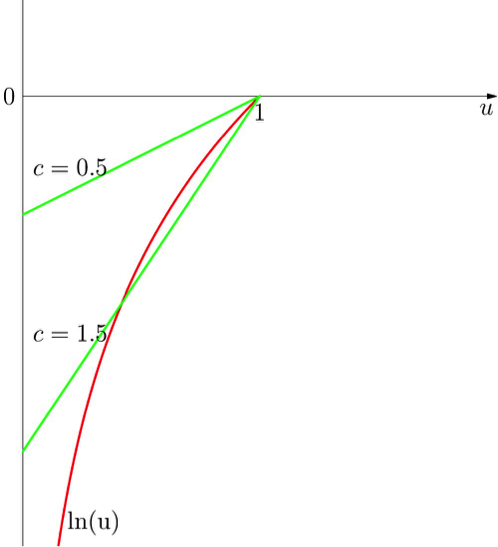
$$\ln(u)=\displaystyle n(\frac{-c}{n}+\frac{c}{n}u)=-c(1-u)$$

圖五該方程式在 $$c>1$$ 時有兩個解，其中一個小於 $$1$$。（本文作者林蔚廷繪）

我們注意到，這個方程在 $$c<1$$ 的時候只有一個解 $$u=1$$；當 $$c>1$$ 的時候有其它解（圖五）。換言之，如果 $$c<1$$，社交網路中幾乎沒有人會處在最大的傳染通路,即所有通路都遠遠小於 $$n$$（當 $$n$$ 很大時，這比例趨近於 $$0$$）；相反，如果平均每個人都至少傳染（或被傳染）一個人 ($$c>1$$)，那麼傳染病就可以在大型社交網路中爆發（傳染通路的大小和 $$n$$ 在一個量級）。

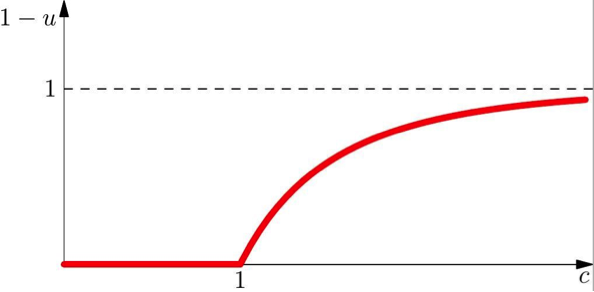
如果我們把最大的傳染通路相對於總人數的比例，也就是任選一人在最大通路中的機率 $$1-u$$，對參數 $$c$$（每個人平均傳染人數）作圖（圖六），我們就可明顯看到在 $$c=1$$ 這個點，曲線有個明顯的轉折，代表爆發的開始。這個點就是這個模型的臨界點。