滲流（上）

滲流（上） (Percolation (I))
西北大學物理與天文學系博士生 林蔚廷、西北大學物理與天文學系博士生 楊暘

地下水的流動，傳染病的爆發，這兩個乍看之下完全不同的現象，有什麼共通之處嗎？如果我們細究其微觀的機制，他們的確是完全不同的。地下水的流動顯然與流體力學有關，傳染病屬於生物學與醫學的領域。然而，如果我們只對某些重要的巨觀特徵有興趣，那麼這兩個現象都可以由滲流理論 (percolation theory) 來描述。

讓我們想想地下水是如何流動的。地層大致上是由大小不一的石塊、土壤所組成的。無論具體的成份是什麼，他們都不是整齊劃一地排列的。我們可以想像一堆大小不同的顆粒，毫無規則地堆在一起，地層大概就像這個樣子（圖一）。這些顆粒之間是有隙縫的，水可以在這些隙縫中流動。然而這些隙縫的分佈是毫無規則的，你可以想像地底下如同有著一堆雜亂無章的水管。

圖一 地層結構示意圖。（本文作者林蔚廷繪）

要想瞭解水在這堆水管中流動的細節是極端困難的，這是因為流體力學的方程式本身就很複雜，而這些水管的分佈又是沒有規則的。但是退一步來想，也許我們並不需要瞭解這些細節——我們不在乎水在某個隙縫中的流速是多少這樣的問題。比較關鍵，也比較有趣的問題是，水是否能從一個地方流到另外一個地方。這樣的問題有實際上的重要性，比如說，我們會想知道地表的水是否能流到地下水層中，使得地下水不至於枯竭。

類似的現象也發生在多孔材料 (porous medium) 中。這種材料中有許多孔洞，有些孔洞是相連接的。如果相連接的孔洞夠多，就相當於有了通道，其中的液體就可經由這些通道流到另一個地方。在日常生活中，過濾式咖啡壺 (coffee percolator) 就利用了這樣的過程，使沸騰的水通過咖啡粉中的隙縫滲流至壺中。早期的滲流理論研究者因此把這類現象稱做 percolation。

想要研究這個過程，首先要知道這些「水管」或通道是如何分佈的。然而無論是土壤還是咖啡粉的堆疊都是雜亂無章的，我們不可能知道精確的分佈。但也正因為這個分佈似乎相當隨機，一個最簡單的模型就是假設這些通道是完全隨機分佈的！事實上，我們將會看到，這麼簡單的模型會有非常有趣的行為。

首先，我們想像用一些整齊排列的方格來劃分地層（圖二），地層中大小不一的顆粒可以佔據一個或多個格子。格子的邊可以是「開放」的——代表可供水流通的隙縫；反之，則處於「閉塞」的狀態。這些隙縫可以串聯在一起，形成一條條的通路。如果存在一條聯通了地層最上層和最下層的通路，那麼我們就說發生了滲流 (percolate)，即是，水可以從表層的土壤流到地下的水層中。

圖二 方格模型示意圖。（本文作者林蔚廷繪）

假設這些方格的每一條邊，處在開放狀態的機率都為 $$p$$。這就好像我們為每一條邊擲一次硬幣，用正反面決定它是開放的還是閉塞的。這裡，我們隨機選取一個 $$0$$ 到 $$1$$ 之間的數，如果這數小於 $$p$$，則代表這邊是開放的，反之則是閉塞的（圖三）。我們的問題是，給定距離很遠的兩個點，存在一條連接兩點的通路的機率是多少呢？

圖三 電腦模擬 p=0.55 的結果，可見到大型的聯通網路。（本文作者林蔚廷繪）

假設地層很大，則這個系統就約略具有平移對稱性（亦即沒有哪個點是特殊的），我們可以令其中的一點為原點。原來的問題就等價於，任意取某一點，該點與原點相聯通的機率為何。這相當於問與原點相聯通的的點佔了多少比例。這個機率或比例，稱之為滲流機率 (percolation probability)。

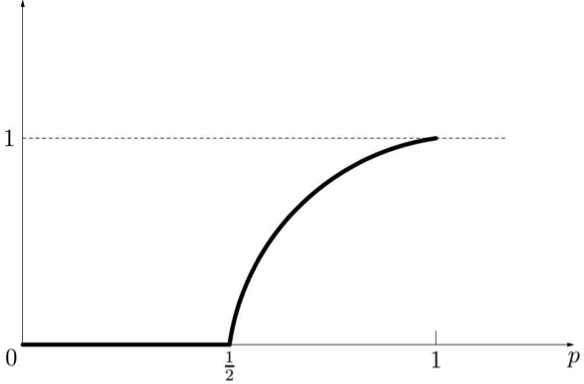
如圖四所示，假設這些格子的數目非常大，當 $$p<\frac{1}{2}$$ 的時候，滲流機率幾乎是 $$0$$！也就是說，只要 $$p<\frac{1}{2}$$，無論怎樣提高 $$p$$ 的值（即使從 $$\frac{1}{30}$$ 上升到 $$\frac{1}{3}$$，提高 $$10$$ 倍），滲流機率並沒有升高一點點。然而，當 $$p>\frac{1}{2}$$ 時，滲流機率會隨 $$p$$ 的升高而顯著上升。因此，我們稱 $$p=\frac{1}{2}$$ 為此方格模型的滲流臨界點。

圖四 滲流機率示意圖。（本文作者林蔚廷繪）

臨界點通常代表系統經歷了相變 (phase transitions)，也就是，系統的巨觀狀態在某個參數微弱改變的時候，發生了突然 的改變。我們最熟悉的例子就是水結成冰的過程。在標準大氣壓下，攝氏 0 度就是水相和冰相的臨界點。在滲流理論中，臨界點則是「不可流通」與「可流通」兩種巨觀狀態的分界。要注意的是，即使對於最簡單的滲流模型，如果我們換一種格子來代表土壤，臨界點也會發生變化。

以上的討論，表示當隙縫太過稀少時，水是不可能在地層中流動的。這樣突然的轉變，也存在其他的系統中。一個著名的例子，就是流行病的傳染。想像現在社會上有某種傳染病，一開始只有少數幾個人感染。如果社會中人際關係過於緊密的話，病原很容易藉由人與人的接觸而散播開來，進而爆發大流行。反過來說，如果人際關係不那麼緊密，感染就不容易爆發。我們將在文章的下半部分，討論一個簡單的流行病模型。

連結：滲流（下）

參考文獻

1. Sahimi, M. (1994). Applications of percolation theory. London: Taylor & Francis.
2. Newman, M. (2010). Networks. Oxford: Oxford University Press.