波耳半徑

波耳半徑 (Bohr Radius)
國立臺灣大學物理學系 簡嘉泓

丹麥物理學家波耳 (Niels Bohr, 1885-1962) 於 1913 年針對原子的內部結構提出了「波耳模型」，其中重要的假設為：

1. 角動量的量子化：原子中電子的角動量為「約化浦朗克常數」(Reduced Planck Constant) 的整數倍，即 $$L=mvr=n\hbar$$
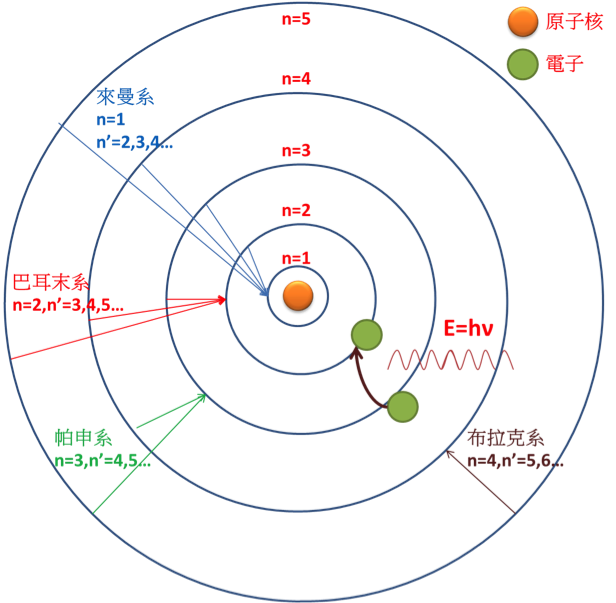
2. 原子內的電子僅能存在於一系列固定的能量狀態（即能階），原子如有任何形式的能量改變，則必在兩能階之間以「躍遷」的方式進行，而由於這些能量是固定的，因此可視為電子會因持有的能量不同，而在特定的距離環繞原子核運轉。將此情形應用到氫原子上，電子在允許的最低能量所繞行氫原子核的距離，即為「波耳半徑」，如下圖中 n = 1 的部分。

圖一、波耳模型、電子躍遷及各線系。（本文作者簡嘉泓繪）

波耳半徑之公認值為 $$0.52917721067\times 10^{-10}~~~m$$（科學技術數據委員會CODATA 2014），約 0.53 Å，代號為 $$a_0$$ 或 $$a$$，此距離也可視為在波耳模型下的基態氫原子中，電子最可能存在的距離。（此距離雖以「波耳模型」為前題所得出，但與解氫原子的薛丁格方程式之結果相同）

若以其他物理常數表示，則：

$$\displaystyle a_0=\frac{4\pi\varepsilon_0\hbar^2}{m_ee^2}=\frac{\hbar}{m_ec\alpha}$$

其中：

$$\varepsilon_0$$ 為真空電容率，其值為 $$8.854187817\times 10^{-12}~(F\cdot m^{-1})$$
$$\hbar$$ 為約化卜朗克常數，為浦朗克常數除上 $$2\pi$$，約為 $$1.05\times 10^{-34}~(J\cdot s)$$
$$m_e$$為電子質量，約為 $$9.11\times 10^{-31}~(kg)$$
$$e$$ 為電子電量，其值為 $$-1.6\times 10^{-19}~(C)$$
$$c$$ 為真空中之光速，約為 $$3\times 10^8~(m/s)$$
$$\alpha$$ 為精細結構常數，約 $$1/137$$，即 $$7.3\times 10^{-3}$$

推導

1. 以古典的圓周運動做為電子繞原子核運動的模型，由於電子與質子的電量皆為 $$1$$ 電子電荷 $$e$$，假設繞行半徑為 $$r$$，我們可以計算出庫侖靜電力，並以圓周運動的加速度為 $$\frac{v^2}{r}$$ 代入。

$$\displaystyle {F_e}=\frac{1}{4\pi\varepsilon_0}\times\frac{e^2}{r^2}$$（向心）$$\displaystyle=m_e\times\frac{v^2}{r}$$

2. 經過移項算出 $$v$$。

$$\displaystyle v=\sqrt{\frac{1}{4\pi\varepsilon_0}\frac{e^2}{rm_e}}$$

3. 代入波耳模型的假設─角動量的量子化 $$L=m_evr=n\hbar$$，可得：

$$\displaystyle v=\frac{n\hbar}{m_er}$$

4. 將步驟二與步驟三比較後移項。

$$\displaystyle r=4\pi\varepsilon_0\frac{n^2\hbar^2}{m_ee^2}$$

5. 最後將 $$n=1$$ 代入，得到波耳半徑。（當 $$n=1$$ 時 $$r=a_0$$ ）

$$\displaystyle a_0=\frac{4\pi\varepsilon_0\hbar^2}{m_ee^2}=\frac{\hbar}{m_ec\alpha}$$ （其中 $$\displaystyle\alpha=\frac{e^2}{4\pi\varepsilon_0\hbar c}$$）

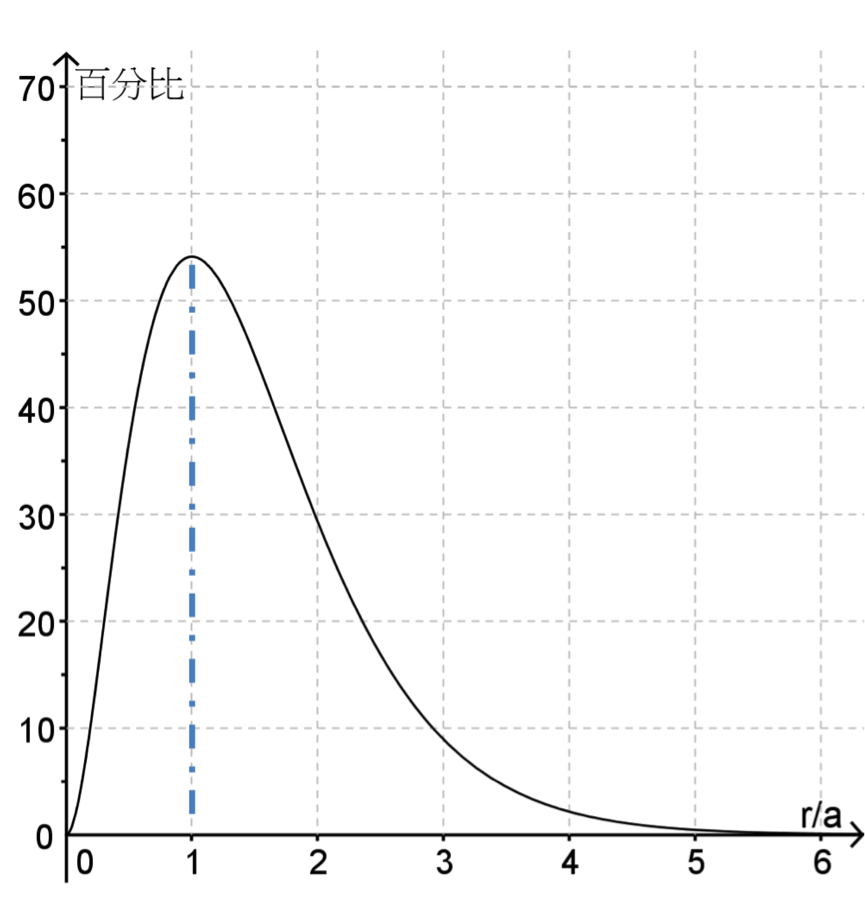
若將基態氫原子的波函數解出並計算最可能找到電子的距離（如下圖），也可以得到類似結果（在 $$r=a_0$$ 時最可能找到電子）。

圖二、氫原子的電子距離。（本文作者簡嘉泓繪）

參考文獻

1. Bohr radius value (CODATA, 2014), NIST Reference on Constants, Units, and Uncertainty. http://physics.nist.gov/cgi-bin/cuu/Value?bohrrada0
2. Bohr radius — Wikipedia. https://en.wikipedia.org/wiki/Bohr_radius
3. Sarazin, F. (2015), The Bohr Model, Modern Physics — Honors, Lecture 9, Colorado School of Mines. http://inside.mines.edu/~fsarazin/phgn310/PDFs/AtomStrucLect2.pdf
4. Carter, R., Derivation of Bohr’s Equations for the One-electron Atom, General Chemistry, The University of Massachusetts Boston. http://alpha.chem.umb.edu/chemistry/ch115/carter/files/103more/BohrEquations.pdf