井字上翻烏龜(A Turtle Game)
國立台中女中數學科賴信志老師/國立台灣師範大學數學系許志農教授責任編輯
摘要：旺宏教育基金會從 2002 年開始，每年舉辦「旺宏科學獎」，該基金會認為科學教育的扎根，在高中階段最顯重要，創新獨立的思考如能從高中階段開始培養，學生的創造力及潛力將超乎想 像。旺宏科學獎的獎項有金牌獎､銀牌獎與優等獎，優於金牌獎的作品可得旺宏獎（此獎項可從缺）。這裡所要介紹的這道遊戲來自第三屆旺宏科學獎的旺宏獎作品。
在井字形的九宮格內隨意放置行走或縮頭狀態的九隻烏龜，如下圖所示：
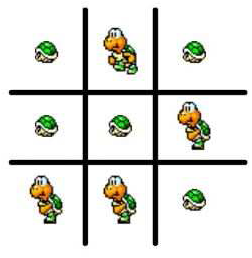每次只能點選其中的一隻烏龜，被點選的烏龜及與其相鄰的烏龜會改變狀態，即行走狀態的烏龜會變成縮頭狀態的烏龜，而縮頭狀態的烏龜會變成行走狀態的烏龜。遊戲的目的就是要將九隻烏龜都變成行走狀態
鋸木板遊戲（The Game of Sawing planks）
國立台中女中數學科賴信志老師/國立台灣師範大學數學系許志農教授責任編輯
鋸木板遊戲源自於許志農教授戲說數學中的一個遊戲，規則如下：給一塊畫有 $$5\times 5$$ 或 $$6\times 6$$ 方格的木板，兩位玩家輪流切割一個單位的長度，先將木板鋸成兩塊者輸。
阿基米德的胃痛拼圖(stomachache puzzle)
國立台中女中數學科賴信志老師/國立台灣師範大學數學系許志農教授責任編輯
摘要：本篇將介紹一道差一點就消失，而且是世界上最古老的拼圖遊戲…胃痛拼圖。
這裡我們將介紹一道差一點就消失，而且是世界上最古老的拼圖遊戲。在加州史丹福大學同步輻射實驗室，古文物復原專家運用紫外光與數位圖像電腦處理技術，讓阿基米德發明的一道遊戲重現天日。
在1998 年10 月30 日，《紐約時報》頭版登了一則報導：紐約佳士得拍賣會上，有一本其貌不揚的古書，以美金 200 萬的高價成交。從外表看，這本書就像是中世紀某位修士的祈禱書，磨損不堪，布滿燒焦、水漬、發霉的痕跡。然而在祈禱文的下方，隱約可看見幾乎被擦拭掉的、傳抄自古代科學家阿基米德的抄本。
四方連塊的正方形拼圖遊戲 (The Puzzle of Tetrominoes)
國立臺中女中數學科賴信志老師/國立臺灣師範大學數學系許志農教授責任編輯
摘要：多方塊的矩形拼圖（Tiling the rectangle）是一個有趣而常見的拼圖遊戲，它的基本規則是：每一種等面積的多方連塊至少都用一個來拼一個矩形。「四方連 塊」（tetrominoes）是指四個單位正方形以邊與邊相連接而成，並扣除圖形旋轉、鏡射，所形成之五種不同形狀的幾何平面圖形。本文探討四方連塊的 拼圖問題。
多方塊的矩形拼圖（Tiling the rectangle）是一個有趣而常見的拼圖遊戲，它的基本規則是：每一種等面積的多方連塊至少都用一個來拼一個矩形。「四方連塊」（tetrominoes）是指四個單位正方形以邊與邊相連接而成，並扣除圖形旋轉、鏡射，所形成之五種不同形狀的幾何平面圖形，如下圖所示，分別為 L 型、Z 型、O 型、I 型、T 型。
多項式函數圖形的遞增、遞減與凹凸性（Increasing, Decreasing, Concave and ConvexProperties of Polynomial Functions）
國立台南第一高級中學數學科林倉億老師/國立臺灣師範大學數學系許志農教授責任編輯
摘要:本文說明多項式函數圖形的遞增、遞減、凹向上、凹向下，以及在區間 上的遞增函數、嚴格遞增函數、遞減函數、嚴格遞減函數、單調函數。
藉助今日科技發展之便，只要打開電腦，執行數學繪圖軟體程式，然後任意輸入一個多項式函數，一瞬間，它的圖形就會顯示在眼前。例如下圖就是利用數學繪圖軟體GeoGebra所繪的 $$f(x)=(x-1)(x-2)(x-3)(x-4)(x-5)$$ 之圖形。
巴斯卡與數學歸納法（Pascal and Mathematical Induction）
國立台南第一高級中學數學科林倉億老師/國立臺灣師範大學數學系許志農教授責任編輯
摘要:本文介紹巴斯卡在其著作《論算術三角形》中的推論12，以及巴斯卡在證明推論12所用的方法與今日數學歸納法的關係。
巴斯卡（Blaise Pascal，1623-1662）因「巴斯卡三角形」而廣為中學學生所認識，然而，大部分中學生以及中學老師並不知道，巴斯卡在《論算術三角形》（A treatise on the Arithmetical Triangle）一書中，除了介紹「算術三角形」（即俗稱的「巴斯卡三角形」）外，還利用了「疑似的」數學歸納法來證明其中的性質，因此，巴斯卡曾被認為是最早使用數學歸納法的人。為什麼說「疑似的」呢？請繼續看下去。
海龍公式的各種證明（下）(The Various Proofs of Heron’s FormulaⅡ)
臺北市立第一女子中學數學科蘇俊鴻老師/國立臺灣師範大學數學系許志農教授責任編輯
連結：海龍公式的各種證明（上）
摘要：本文介紹海龍公式的各種證明。
接著來看李善蘭在《天算或問》中的證法，主要是論述等式 \((s-a)(s-b(s-c)=sr^2\)，成立。然後兩邊再同乘 \(s\)，即得 \(s^2r^2=s(s-a)(s-b)(s-c)\)。
海龍公式的各種證明（上）(The Various Proofs of Heron’s FormulaⅠ)
臺北市立第一女子中學數學科蘇俊鴻老師/國立臺灣師範大學數學系許志農教授責任編輯
摘要：本文介紹海龍公式的各種證明。
現行有關高級中學教材的安排，海龍公式出現在三角函數的學習脈絡中，被當成熟練餘弦定律的典範例（以99 課綱來說在高二上學期）。它的證明過程涉及了教師在三角函數教學會強調的知識與技巧。比如：透過平方關係轉換正餘弦；餘弦值與邊長的關係 \((\cos A=\frac{b^2+c^2-a^2}{2bc})\)；乘法公式的使用。
中國的測量術(下) (The Measurement in China Ⅱ)
台北市立第一女子中學數學科蘇俊鴻老師/國立台灣師範大學數學系許志農教授責任編輯
連結：中國的測量術(上)
摘要: 本文延續中國的測量術(上)繼續介紹中國的測量術。
接續著〈中國的測量術(上)〉，我們來談談『重差法』。什麼是『重差法』？簡單地說，就是利用兩個或兩個以上的表當做測量基準的測量方法。
根據史家吳文俊對《周髀算經》趙君卿注中日高圖的還原，以及利用出入相補原理重新詮釋後，確信趙君卿已經掌握重差法：利用兩個等高的表，分別量得該表的影長，從而得到影差，便能利用其計算日高及日遠。而劉徽則在重差法的基礎上，將它的應用加以推廣。劉徽談到重差法的用處：「凡望極高，測絕深而兼知其遠者必用重差、勾股，則必以重差為率，故曰重差。」更以測日為例，如圖一所示，給出兩個基本公式：
中國的測量術 (上) (The Measurement in China I)
台北市立第一女子中學數學科蘇俊鴻老師/國立台灣師範大學數學系許志農教授責任編輯
摘要：本文介紹中國的測量術。
一談起測量方法，大家腦中馬上浮現「三角測量」─藉助三角函數的幫助，我們只要測量出某些長度及角度，就能處理那些我們無法實際量測的問題。這也是數學教師在三角函數的學習上，用來強化三角函數學習「正當性」的最佳理由。