行列式的應用

行列式的應用（Applications of Determinant）
國立臺南第一高級中學林倉億老師

連結：行列式的性質

以下介紹行列式在高中數學中主要的應用：

1. 表示平面上三角形的面積
   \(\vec{OA}=(a_1,b_1)\)、\(\vec{OB}=(a_2,b_2)\)，則 \(\Delta OAB\) 面積 \(= \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\)
   （\(\frac{1}{2}\) 乘以 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\) 的絕對值）。
   【證明】：
   由三角形面積公式 \(\Delta OAB = \frac{1}{2}\sqrt {{{\left| {\vec{OA}} \right|}^2}{{\left| {\vec{OB}} \right|}^2} – {{\left( {\vec{OA} \cdot\vec{OB}} \right)}^2}}\)
   可得
   \(\begin{array}{ll}\Delta OAB &= \frac{1}{2}\sqrt {({a_{ 1}}^2 + {b_{ 1}}^2)({a_{ 2}}^2 + {b_{ 2}}^2) – {{\left( {{a_{ 1}}{a_{ 2}} + {b_{ 1}}{b_{ 2}}} \right)}^2}} \\&= \frac{1}{2}\sqrt {{a_{ 1}}^2{b_{ 2}}^2 + {a_{ 2}}^2{b_{ 1}}^2 – 2{a_{ 1}}{a_{ 2}}{b_{ 1}}{b_{ 2}}} = \frac{1}{2}\sqrt {{{\left( {{a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}} \right)}^2}} \\&= \frac{1}{2}\sqrt { {{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}^2}} = \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\end{array}\)
2. 表示空間中兩不平行向量的外積
   \(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，則 \(\vec{OA}\) 與 \(\vec{OB}\) 的外積
   可記作 \(\vec{OA}\times\vec{OB}= ( \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| )\) 
3. 表示空間中三角形面積
   \(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，
   則 \(\Delta OAB\) 面積 \(=\frac{1}{2}|\vec{OA}\times\vec{OB}|= \frac{1}{2}\sqrt { {{\left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right|}^2} + {{\left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right|}^2} + {{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}^2}} \)
   【證明】：
   
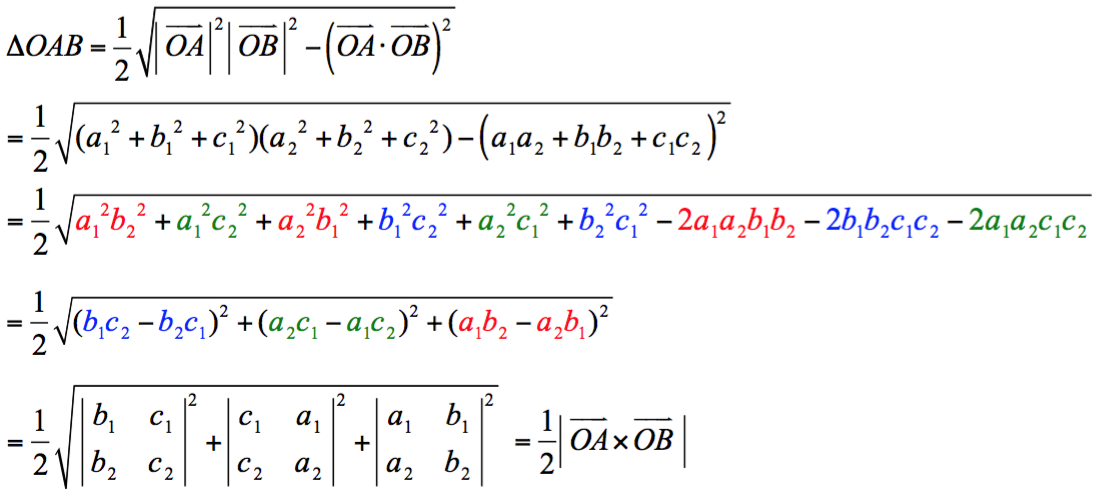
4. 表示空間中三向量所展成的平行六面體體積
   \(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，\(\vec{OC}=(a_3,b_3,c_3)\)，則 \(\vec{OA}\)、\(\vec{OB}\)、\(\vec{OC}\) 在空間中所展成的平行六面體體積為 \(\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right|} \right|\) （\(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right|\) 的絕對值）。
   【證明】：
   \(\vec{OA}\)、\(\vec{OB}\)、\(\vec{OC}\) 在空間中所展成的平行六面體體積公式為 \(V=|\vec{OC}\cdot(\vec{OA}\times \vec{OB})|\)，
   又 \(\vec{OA}\times\vec{OB}=( \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| )\)，
   代入可得
   
5. 平面上三相異直線恰交於一點的條件
   \(L_1:a_1x+b_1y=c_1\)、\(L_2:a_2x+b_2y=c_2\)、\(L_2:a_2x+b_2y=c_2\)
   為平面上互異的三條直線，若此三條直線恰交於一點，則 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| = 0\)。
   （其逆不真，反例是三平行直線依然具有此條件，所以三條相異直線方程式係數所成的行列式為 \(0\)，並不能保證三條直線恰交於一點。）
   【證明】：
   由二階克拉瑪公式可知 \(L_1:a_1x+b_1y=c_1\) 與 \(L_2:a_2x+b_2y=c_2\) 的交點坐標
   為 \(( \frac{{\left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{b_{ 1}}}\\ {{c_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}}{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}} , \frac{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{c_{ 2}}} \end{array} } \right|}}{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}} )\)，代入 \(L_3:a_3x+b_3y=c_3\)，
   得 \({a_3} \cdot \frac{{\left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{b_{ 1}}}\\ {{c_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}}{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}} + {b_3} \cdot \frac{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{c_{ 2}}} \end{array} } \right|}}{{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}} = {c_3}\)，兩邊同乘以 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\)，
   再移項得 \({a_3} \cdot \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{b_{ 1}}}\\ {{c_{ 2}}}&{{b_{ 2}}} \end{array} } \right| + {b_3} \cdot \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{c_{ 2}}} \end{array} } \right| – {c_3}\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = 0\)，
   利用行列式的性質，可再寫成 \({a_3} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| – {b_3} \cdot \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{c_{ 2}}} \end{array} } \right| + {c_3}\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = 0\)，
   等號左邊其實就是 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right|\) 依第 \(3\) 列降階展開的結果，
   故得證 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| = 0\)。
6. 二階方陣可逆的充要條件
   \(A = \left[ { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right]\)，定義 \(\det A = \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\)。\(A\) 為可逆方陣 \(\Leftrightarrow \det A=0\)。
   【證明】：
   \(A = \left[ { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right]\) 為可逆方陣，故存在唯一非零方陣 \(\left[ { \begin{array}{*{20}{c}} {{x_{ 1}}}&{{x_{ 2}}}\\ {{y_{ 1}}}&{{y_{ 2}}} \end{array} } \right]\) 使得
   \(\left[ { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right] \cdot \left[ { \begin{array}{*{20}{c}} {{x_{ 1}}}&{{x_{ 2}}}\\ {{y_{ 1}}}&{{y_{ 2}}} \end{array} } \right] = \left[ { \begin{array}{*{20}{c}} 0&0\\ 0&0 \end{array} } \right]\\\Leftrightarrow \left[ { \begin{array}{*{20}{c}} {{a_{ 1}}{x_{ 1}} + {b_{ 1}}{y_{ 1}}}&{{a_{ 1}}{x_{ 2}} + {b_{ 1}}{y_{ 2}}}\\ {{a_{ 2}}{x_{ 1}} + {b_{ 2}}{y_{ 1}}}&{{a_{ 2}}{x_{ 2}} + {b_{ 2}}{y_{ 2}}} \end{array} } \right] = \left[ { \begin{array}{*{20}{c}} 0&0\\ 0&0 \end{array} } \right]\)
   \(\Leftrightarrow \left\{ \begin{array}{l} {a_{ 1}}{x_{ 1}} + {b_{ 1}}{y_{ 1}} = 0\\ {a_{ 2}}{x_{ 1}} + {b_{ 2}}{y_{ 1}} = 0 \end{array} \right.\) 與 \(\left\{ \begin{array}{l} {a_{ 1}}{x_{ 2}} + {b_{ 1}}{y_{ 2}} = 0\\ {a_{ 2}}{x_{ 2}} + {b_{ 2}}{y_{ 2}} = 0 \end{array} \right.\) 這兩個方程組都有非 \((0,0)\) 之解
   \(\Leftrightarrow \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = 0\Leftrightarrow \det A = 0\)
7. \(n\) 階方陣可逆的充要條件
   可以將6.推廣到 \(n\) 階方陣，即 \(A = \left[ { \begin{array}{*{20}{c}} {{a_{ 11}}}&{{a_{ 12}}}&{{a_{ 13}}}& \cdots &{{a_{ 1n}}}\\ {{a_{ 21}}}&{{a_{ 22}}}&{{a_{ 23}}}& \cdots &{{a_{ 2n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{a_{ n1}}}&{{a_{ n2}}}&{{a_{ n3}}}& \cdots &{{a_{ n{\kern 1pt} n}}} \end{array} } \right]\) 為 \(n\) 階方陣，\(n\ge 3\)，定義  \(\det A = \left| { \begin{array}{*{20}{c}} {{a_{ 11}}}&{{a_{ 12}}}&{{a_{ 13}}}& \cdots &{{a_{ 1n}}}\\ {{a_{ 21}}}&{{a_{ 22}}}&{{a_{ 23}}}& \cdots &{{a_{ 2n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{a_{ n1}}}&{{a_{ n2}}}&{{a_{ n3}}}& \cdots &{{a_{ n{\kern 1pt} n}}} \end{array} } \right|\)。
   【證明】：仿6.之證明，略。