2sp2混成軌域的解析 (下)

2sp$$^2$$ 混成軌域的解析 (下) The analysis of 2sp$$^2$$ hybrid orbitals (III)
國立臺灣師範大學化學系兼任教授 邱智宏教授

連結：$$2sp^2$$ 混成軌域的解析 (中)

三、$$2sp^2$$ 軌域的等高線圖

圖一中三個 $$2sp^2$$ 軌域的等高線圖，若依據(式-4)、(式-6)和(式-7)實際在Excel軟體上繪圖，其所得的結果是不是與圖一相同？ 若將 $$2s$$、$$2p_y$$ 的波函數代入混成軌域(式-4)中，可得下式：

$$\begin{multline*}\varphi_{2sp^2(1)}=-\frac{1}{\sqrt{3}}\left[\frac{1}{4(2\pi)^{\frac{1}{2}}}(\frac{Z}{a_0})^{\frac{3}{2}}\left(2-\frac{Zr}{a_0}\right)e^{-\frac{Zr}{2a_0}}\right]\\+\frac{\sqrt{2}}{\sqrt{3}}\left[\frac{1}{4(2\pi)^{\frac{1}{2}}}(\frac{Z}{a_0})^{\frac{5}{2}}re^{-Zr/2a_0}\sin\theta\sin\phi\right] \end{multline*}$$

$$\begin{multline*}\varphi_{2sp^2(1)}=\frac{1}{4\sqrt{3}(\pi)^{1/2}}(\frac{Z}{a_0})^{\frac{3}{2}}\left[-\left(2-\frac{Zr}{a_0}\right)+\sqrt{2}(\frac{Z}{a_0})r\sin\theta\sin\phi\right]e^{-\frac{Zr}{2a_0}} \end{multline*}$$

若將上式等號右邊中括號前的常數項省略，因為這樣做並不會影響軌域的形狀，另外將極座標轉換成直角座標， $$y=r\sin\theta\sin\phi$$，另外，因為是在 $$xy$$ 平面上，$$z=0$$，所以 $$r=(x^2+y^2)^{1/2}$$，因此可得下列(式-14)，式中大寫的 $$Z$$ 代表核電荷數，並非代表座標值的小寫 $$z$$。

$$\displaystyle\begin{multline*}\varphi_{2sp^2(1)}=\left[-\left(2-\frac{Z(x^2+y^2)^\frac{1}{2}}{a_0}\right)+\sqrt{2}(\frac{Z}{a_0})y\right]e^{-\frac{Z(x^2+y^2)^{\frac{1}{2}}}{2a_0}}\end{multline*}$$  (式-14)

若利用Excel軟體依照(式-14)畫出 $$2sp^2(1)$$ 軌域在 $$xy$$ 平面上的等高線圖，詳如圖六所列。

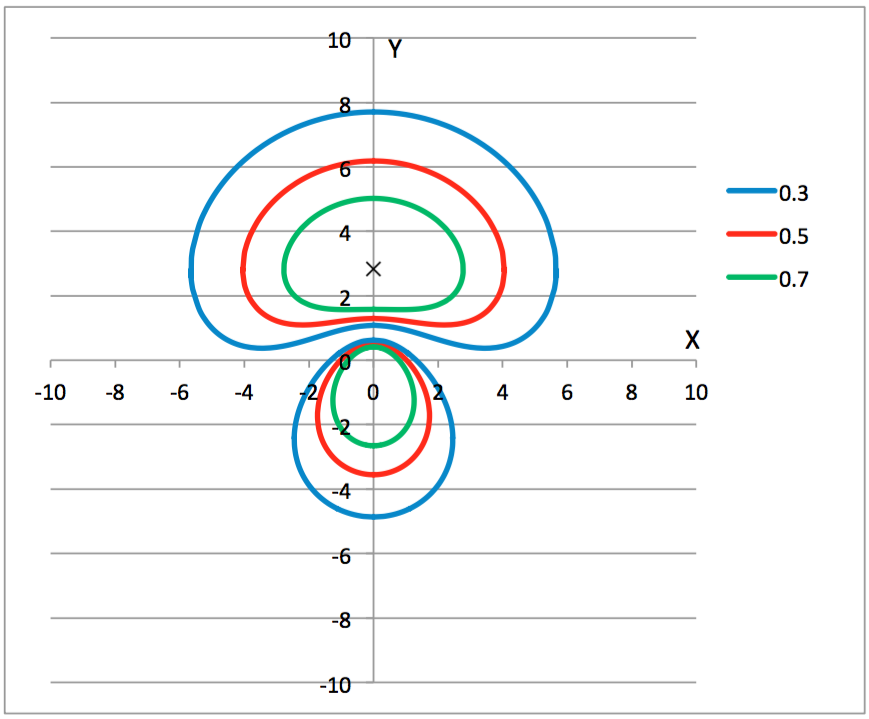
圖六 依(式-14)畫出 $$\varphi_{2sp(1)}$$ 軌域的等高線圖，實線部分波函數為正，虛線部分為負，圖中的x號，標示為波函數的極大值。藍、紅、綠的等高線分別代表其波函數的數值等於極大值的0.3、0.5及0.7倍。 (來源：作者繪製)

圖中的x號，為波函數極大值的位置，而藍、紅、綠的等高線分別代表其波函數的數值等於極大值的 $$0.3$$、$$0.5$$ 及 $$0.7$$ 倍，其中實線的部份波函數為正值，虛線部份為負值。由圖中可看出上邊的等高線，由於 $$2s$$ 和 $$2p$$ 加成的關係形狀變大，下邊的由於互相抵消的緣故形狀變小。此圖形的樣式和圖一相互比較，可發現雖大同卻有小異，例如節面並没有通過原點、原點出現在波函數為負值的小楕圓形內、右邊等高線的形狀並不是楕圓形。

$$\varphi_{2sp^2(2)}$$ 軌域在 $$xy$$ 平面上的等高線圖，也可利用相同的方法處理，將 $$2s$$、$$2p_y$$ 及 $$2p_x$$ 的波函數代入(式-6)中，經過整理並將極座標轉換成直角座標可得下式：

$$\begin{multline*}\varphi_{2sp^2(2)}=\frac{1}{4(6\pi)^{\frac{1}{2}}}(\frac{Z}{a_0})^{\frac{3}{2}}\left[-\left(2-\frac{Z(x^2+y^2)^\frac{1}{2}}{a_0}\right)-\frac{1}{\sqrt{2}}\times\left(\frac{Z}{a_0}\right)y+\frac{\sqrt{3}}{\sqrt{2}}\times\left(\frac{Z}{a_0}\right)x\right]e^{-\frac{Z(x^2+y^2)^{\frac{1}{2}}}{2a_0}}\end{multline*}$$

若利用Excel軟體依照(式-6)畫出 $$2sp^2(2)$$ 軌域在 $$xy$$ 平面上的等高線圖，詳如圖七所列。

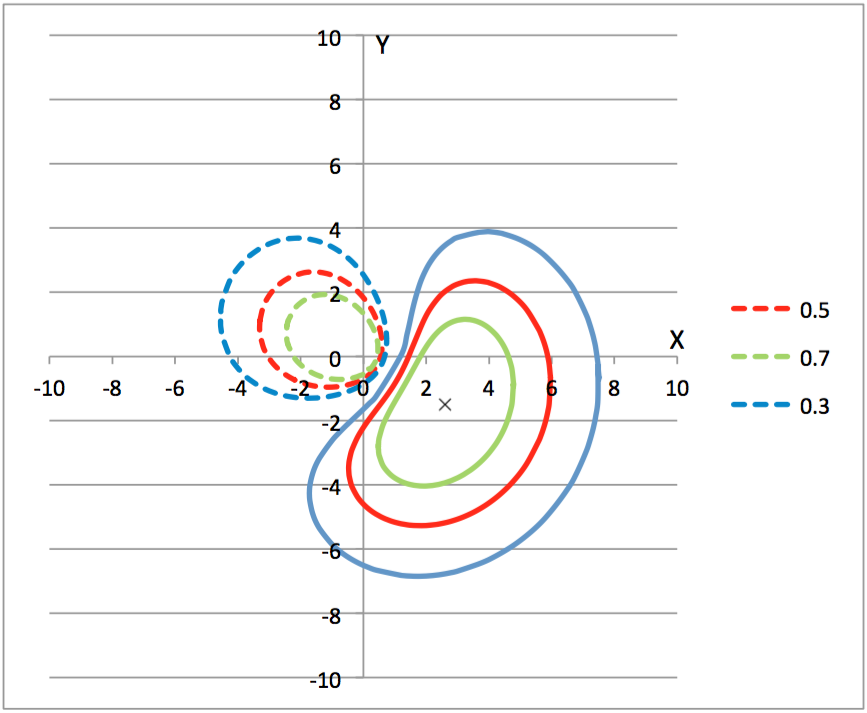
圖七 依(式-6)畫出 $$\varphi_{2sp(2)}$$ 軌域的等高線圖，實線部分波函數為正，虛線部分為負，圖中的x號，標示為波函數的極大值。藍、紅、綠的等高線分別代表其波函數的數值等於極大值的0.3、0.5及0.7倍。(來源：作者繪製)

比較(式-4)和(式-6)兩者的波函數似乎差別頗大，但是由圖六和圖七比較則不然，若將圖六順時鐘旋轉 $$120$$ 度即為圖七，相同地，利用(式-7)所畫的等高線圖，應該和圖七再順時鐘旋轉 $$120$$ 度一樣，此三者為等價卻方位不同的軌域。

接著若以氣相的 $$\mathrm{BH_3}$$ 為例，一般普化的教科書均價殼層電子排斥理論(VSEPR)來解釋分子的形狀。所謂VSEPR的理論即為分子內所有價殼層內的電子對，彼此間互有排斥力，因此若能將這些電子對安排在彼此距離愈遠的地方，排斥力愈小愈安定，因為 $$\mathrm{BH_3}$$ 恰好有 $$6$$ 個價電子，形成 $$3$$ 個共價鍵，因此其分子應為平面三角形最安定。

本文由軌域波函數計算的結果，中心的 $$\mathrm{B}$$ 原子以 $$3$$ 個 $$2sp^2$$ 軌域，分別和周邊的 $$3$$ 個 $$\mathrm{H}$$ 原子的 $$1s$$ 軌域形成鍵結，由於 $$3$$ 個 $$2sp^2$$ 軌域，分別在平面上以 $$120$$ 度隔開，顯然其形成的分子形狀亦為平面的等邊三角形，此結論和VSEPR所得的結果完全一致。

四、結論

本文利用Excel軟體依據 $$2s$$、$$2p_x$$ 和 $$2p_y$$ 的波函數，畫出相關軌域的等高線圖，並將三者相加、相減後形成混成軌域後的 $$3$$ 個 $$2sp^2$$ 波函數，也畫出其軌域的等高線圖。

由圖中我們發現普化或有機化學的教科書經常將 $$2s$$ 的波函數圖形，以 $$1s$$ 軌域來類比並不正確，例如圖一 $$2s$$ 和 $$2p_y$$ 軌域混成的示意圖中，$$2s$$ 軌域若依照量子力學的計算，應該有一個節球面，分成內外二層，且二者波函數的數值正負號相反，即內層為正值，外層為負值，因此，若和 $$2p_y$$ 形成混成軌域，其正確的混成軌域波函數應表示如(式-4)、(式-6)和 (式-7)才合理。

但是，若經實際計算，$$2s$$ 軌域在節面以內電子所佔的比率，僅為整體的 $$5.3\%$$，因此對於尚未學習物理化學或量化的學生而言，將 $$2s$$ 類比為 $$1s$$ 來處理混成軌域的問題，亦不失為一種簡潔、易懂而合理的假設。另外，真正的 $$2sp^2$$ 軌域並不像圖一所示，應如圖六、圖七的等高線圖，兩邊的形狀除了大小不同、波函數值的符號相反以外，其節球面並没有通過原點、形狀也大相逕庭。最後以氣能 $$\mathrm{BeH_3}$$ 分子為例，其分子的形狀無論是由波函數做線性組合所得的結論，和使用價殼層電子排斥理論所得的結果完全一致。

參考文獻

1. /highscope/?s=%E9%82%B1%E6%99%BA%E5%AE%8F
2. Robert G. Mortimer (2008), Physical Chemistry (3rd ed.). p867~885, Elsevier Academic Press.
3. 葉名倉、劉如熹、邱智宏、周芳妃、陳建華、陳偉民（2012 年）高級中學化學選修上冊。南一書局。第70～74頁。
4. http://wps.prenhall.com/wps/media/objects/340/348272/Instructor_Resources/Chapter_02/Text_Images/FG02_14.JPG