2s 軌域的能階為何比 2p 軌域低？

2s 軌域的能階為何比 2p 軌域低？ Why is the 2s orbital lower in energy than the 2p orbital?
國立臺灣師範大學化學系兼任教授 邱智宏教授

高中化學教授氫原子及多電子原子的軌域能階時，總會告訴學生氫原子 $$2s$$ 和 $$2p$$ 軌域的能階相等，而在多電子原子時則 $$2s$$ 軌域的能階比 $$2p$$ 低，至於為何會有這種現象，老師通常會說這是量子力學計算的結果，以後大家就會知道了。

但是以後真的會知道嗎？即使學過量化 (quantum chemistry) 的學生也未必能清楚的交代來龍去脈，其原因究竟是 $$2s$$ 軌域的平均半徑比 $$2p$$ 小，因而造成 $$2s$$ 的電子和原子核的吸引力較大，或者是另有原因？本文嘗試從源頭的波函數開始推導，提供好奇的學子，除了以後就會知道的另類解答。

一、似氫原子的 $$2s$$、$$2p$$ 波函數及其特性

由薛丁格方程式 (Schrödinger equation) 解出的似氫原子 (hydrogen like atom) $$2s$$、$$2p_z$$ 的波函數分別如下：

$$\displaystyle\varphi_{2s}=\frac{1}{4\sqrt{2\pi}}(\frac{Z}{a_0})^{3/2}\left(2-\frac{Zr}{a_0}\right)e^{-Zr/2a_0}$$      (式1)

$$\displaystyle\varphi_{2p_z}=\frac{1}{4\sqrt{2\pi}}(\frac{Z}{a_0})^{5/2}r\cos\theta e^{-Zr/2a_0}$$      (式2)

其中 $$a_0$$ 為波耳半徑等於 $$\mathrm{0.53\overset{\circ}A}$$，$$Z$$ 為原子核的電荷數。似氫原子的波函數 $$\varphi$$ 可由三部分構成 $$\varphi=R_{nl}(r)\Theta_{lm}(\theta)\Phi_{m}(\phi)$$，其中 $$R_{nl}(r)$$ 為徑向函數 (radial function) 僅和極座標中的 $$r$$ 值有關，和 $$\theta$$、$$\phi$$ 無關。

上列二波函數的徑向函數如下所列，其中  $$2p_x$$、$$2p_y$$、$$2p_z$$ 的徑向函數均相同以 $$2p$$ 表示。

$$\displaystyle R_{2s}=\frac{1}{\sqrt{2}}(\frac{Z}{a_0})^{3/2}\left(1-\frac{Zr}{2a_0}\right)e^{-Zr/2a_0}$$      (式3)

$$\displaystyle R_{2p}=\frac{1}{\sqrt{24}}(\frac{Z}{a_0})^{5/2}re^{-Zr/2a_0}$$      (式4)

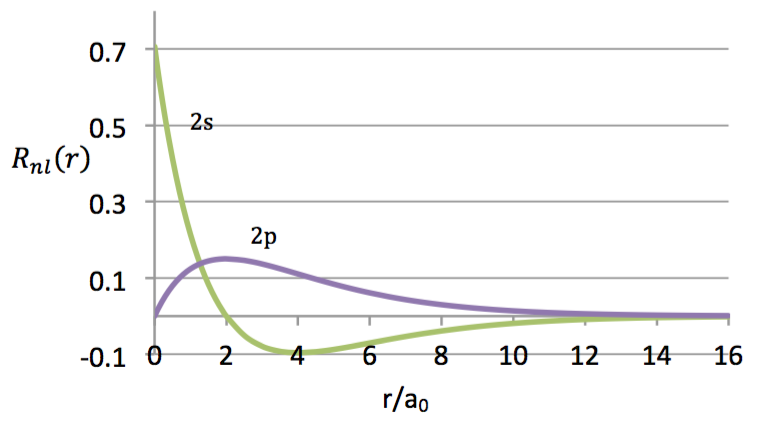
將其徑向函數對半徑作圖可得圖一，其中 $$x$$ 座標的刻度為 $$r/a_0$$。

圖一 氫原子的 $$2s$$ 和 $$2p$$ 徑向函數對 $$r$$ 作圖的比較(來源:作者繪製)

由圖中可看出 $$2s$$ 在 $$r=0$$ 時徑向函數的值最大，隨著 $$r$$ 值的增大遞減的很快，在 $$r=2a_0$$ 的地方出現一個節點，代表此處電子出現的機率為 $$0$$。而 $$2p$$ 在 $$r=0$$ 時徑向函數的值為 $$0$$，但在 $$r=2a_0$$ 的附近出現一個極大值。

若要了解電子出現機率與 $$r$$ 值的關係，則需要藉徑向機率密度函數 ($$P(r)$$, the radial probability density function) 對 $$r$$ 作圖以便觀察，其函數如式 5 所列，將 $$2s$$ 和 $$2p$$ 的徑向函數（式 3 和式 4）代入式五，並利用 excel 軟體直接由式 5 對 $$r$$ 作圖可得圖二。

$$P(r)=|R(r)|^2r^2$$      (式5)

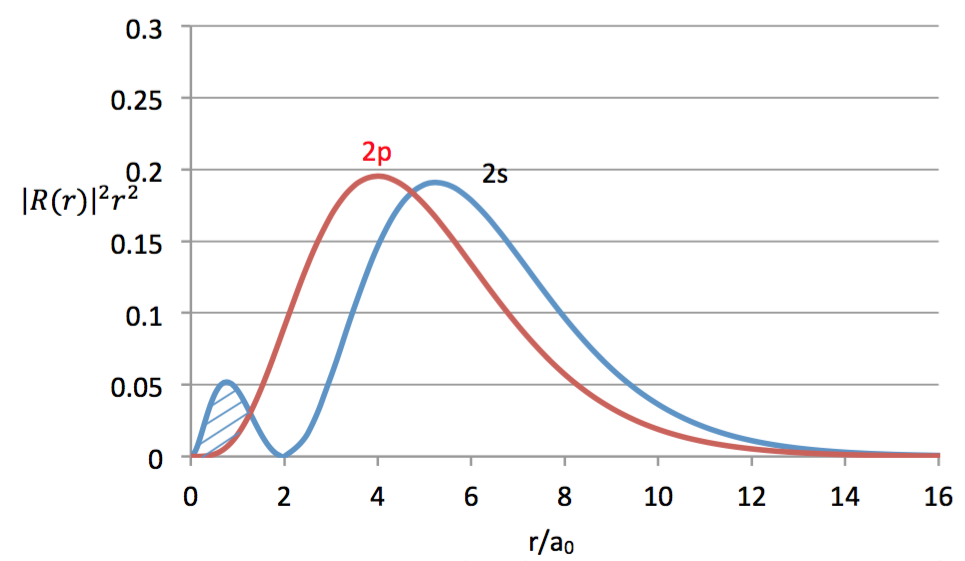
圖二 氫原子的 $$2s$$ 和 $$2p$$ 徑向機率密度函數對 $$r/a_0$$ 作圖的比較。其中畫斜線的區域，即為電子在 $$2s$$ 軌域中比在 $$2p$$ 軌域更接近原子核的部分(來源:作者繪製)

$$2s$$ 圖形呈現二個山峰，二個極大值，有一個節點。而 $$2p$$ 為鐘形分佈，並没有節點出現。圖中畫斜線的部分，是 $$2s$$ 軌域比 $$2p$$ 更接近原子核的部分。有了這些基本了解以後，我們開始來探究多電子原子的 $$2s$$ 軌域能階為何較 $$2p$$ 低，是因為平均半徑較近呢？還是另有原因？

二、似氫原子 $$2s$$、$$2p$$ 軌域平均半徑的比較

接下來要如何計算似氫原子 $$2s$$ 和 $$2p$$ 軌域的平均半徑？在量子力學中要求出某一物理量 $$(A)$$ 的期望值（expectation value，即為平均值），常以下式表示：

$$<A>=\int\varphi^{*}~\hat{A}~\varphi ~dV$$      (式6)

在式 6 中， $$\varphi$$ 為正規化的波函數， $$\hat{A}$$ 為運算子 (operator)，$$dV$$ 為單位體積，在極座標系統中等於 $$dV=r^2\sin\theta~dr~d\emptyset~d\theta$$。因此欲求 $$2s$$ 軌域的平均半徑 $$<r>$$ 亦可表示如下：

$$\begin{array}{ll}\displaystyle<r_{2s}>&=\displaystyle\int\varphi^{*}_{2s}~r~\varphi_{2s}~dV=\iiint r~|\varphi_{2s}|^2~r^2~\sin\theta~dr~d\emptyset~d\theta\\&=\displaystyle\int^{\infty}_0r^3~|\varphi_{2s}|^2~dr~\int^{2\pi}_0d\emptyset~\int^{\pi}_0\sin\theta~d\theta\end{array}$$

$$<r_{2s}>=\displaystyle\int^{\infty}_0r^3\left(\frac{1}{4\sqrt{2\pi}}(\frac{Z}{a_0})^{3/2}\left(2-\frac{Zr}{a_0}\right)e^{-Zr/2a_0}\right)^2dr\times(2\pi)\times(2)$$

$$\displaystyle<r_{2s}>=\frac{Z^3}{8a^{3}_0}\left(\int^{\infty}_{0}4r^3e^{-\frac{Zr}{a_0}}dr-\int^{\infty}_{0}\frac{4Zr^4}{a_0}e^{-\frac{Zr}{a_0}}dr+\int^{\infty}_{0}\frac{Z^2r^5}{a^{2}_{0}}e^{-\frac{Zr}{a_0}}dr\right)$$

對於上式的積分式，可利用下列公式求解：

$$\displaystyle\int^{\infty}_{0}x^ne^{-\alpha x}~dx=\frac{n!}{\alpha^{n+1}}$$

$$\displaystyle<r_{2s}>=\frac{Z^3}{8a^{3}_{0}}\left[4\times\frac{3!}{(Z/a_0)^4}-\frac{4Z}{a_0}\times\frac{4!}{(Z/a_0)^5}+\frac{Z^2}{a^{2}_0}\times\frac{5!}{(Z/a_0)^6}\right]=\frac{6a_0}{Z}$$

由上列計算可知似氫原子的平均半徑為 $$(6a_0)/Z$$，核電荷愈大時，平均半徑愈小，電子愈接近原子核。$$2p$$ 軌域的得平均半徑亦可經由上列相同的計算方式求得，以 $$2p_z$$ 為例如下：

$$\begin{array}{ll}<r_{2p_z}>&=\displaystyle\int\varphi^{*}_{2p_z}~r~\varphi_{2p_z}~dV\\&=\displaystyle\frac{1}{32\pi}(\frac{Z}{a_0})^5\int^{\infty}_{0}r^5e^{-Zr/a_0}dr\int^{2\pi}_{0}d\emptyset\int^{\pi}_0\sin\theta\cos^2\theta d\theta\\&=\displaystyle\frac{1}{32\pi}(\frac{Z}{a_0})^5\left(\frac{5!}{(Z/a_0)^6}\right)(2\pi)(\frac{2}{3})=\frac{5a_0}{Z}\end{array}$$

若計算 $$2p_x$$ 和 $$2p_y$$，其結果也相同，因此似氫原子 $$2p$$ 軌域的平均半徑為 $$5a_0/Z$$。將 $$2p$$ 和 $$2s$$ 相互比較，顯然 $$2s$$ 軌域的平均半徑比 $$2p$$ 長 $$a_0/Z$$，單就此而論 $$2s$$ 軌域的能階若低於 $$2p$$，平均半徑就不會是主要原因，那麼在多電子原子中造成 $$2s$$ 軌域的能量低於 $$2p$$ 真正因素為何？

三、屏蔽效應

在多電子原子的系統中（原子序為 $$Z$$），當內層軌域填有電子時，外層電子感受到原子核的正電荷會低於 $$Z$$ 值，其原因為內層電子將部分原子核的正電荷抵消，產生屏蔽的效果，使外層電子佔據的軌域位能增加，此現象稱為屏蔽效應 (shielding effect)。

在多電子原子系統中，例如 Li 原子，當 $$2$$ 個電子填在內層的 $$1s$$ 軌域後，第 $$3$$ 個電子填在 $$2s$$ 和 $$2p$$ 有什麼差別？若填在 $$2s$$ 軌域中，則如圖二所示，電子會有部分的機率穿透 $$1s$$，因而更靠近原子核，使屏蔽效應並不這麼明顯。反觀電子若填在 $$2p$$ 軌域，則此穿透的影響較小，使得內層電子有更好的屏蔽效應，因此其軌域的位能比 2s 高，至於 $$3s$$ 和 $$3p$$ 或主量子數更高的能階也會出現相同的結果。

四、結論

本文探討多電子原子系統中，$$2s$$ 軌域能量低於 $$2p$$ 的原因。由文中的推導可知造成此結果的主要因素並非軌域的平均半徑，因為 $$2p$$ 軌域的平均半徑比 $$2s$$ 還小。屏蔽效應反而是主要因素，ns 軌域具有穿透內層軌域的能力，因此造成屏蔽效應減弱，軌域的能階因而降低。

至於似氫原子因為只有一個電子，不論填在 $$2s$$ 或 $$2p$$ 軌域，內層軌域均無電子當然也不會有屏蔽效應。另外，細心的讀者會發現，推導的過程均以似氫原子為基礎，其結論是否可直接類比在多電子原子，事實上除了似氫原子的薛丁格方程式有正確解以外，其他三體的薛丁格方程式均為近似解，因此使用似氫原子做類比亦不失為一種變通的方式。

參考文獻

1. Levine, I. N.(1988), Physical Chemistry (3rd ed.). p622~632, McGRAW-HILL Book Company.
2. 葉名倉、劉如熹、邱智宏、周芳妃、陳建華、陳偉民（2013 年）高級中學化學選修上冊。南一書局。第19～33頁。
3. Why is the 2s orbital lower in energy than the 2p orbital when the electrons in 2s are usually farther from the nucleus? — chemistry.stackexchange.com. http://chemistry.stackexchange.com/questions/152/why-is-the-2s-orbital-lower-in-energy-than-the-2p-orbital-when-the-electrons-in
4. Quantum calculations for Hydrogen — http://sethi.lamar.edu. http://www.cobalt.chem.ucalgary.ca/ziegler/Lec.chm373/tuwa8.pdf
   http://sethi.lamar.edu/bahrim-cristian/Courses/PHYS3350/3350-PROBLEMS/Quantum_H_1.pdf