馬克士威-波茲曼分布

馬克士威-波茲曼分布 (Maxwell-Boltzmann distribution)
國立臺灣大學物理系 羅雅琳 博士後研究員

所謂的分布函數 (distribution function)是指當一個由多粒子所組成的物理系統處在絕對溫度T時，在系統達熱平衡的狀態下，粒子處在某一能量狀態的機率分布，而常見的分布函數有三種，即用於描述費米子 (fermion)的費米-狄拉克分布函數(Fermi-Dirac distribution function)、用於描述玻色子(boson)的玻色-愛因斯坦分布函數(Bose-Einsein distribution)、以及常用於描述全同且可分辨之古典粒子的馬克士威-波茲曼分布函數[1]。

馬克士威-波茲曼分布函數是以物理學家馬克士威和波茲曼命名[2]。此分布函數常用於描述氣體分子等古典粒子的統計分布。雖然不同粒子間具有全同性（即粒子的本徵物理特性相同，像是粒子之質量、電荷、自旋等），但假設不同粒子間可被分辨，也就是說可將所有粒子編號且每個粒子可用牛頓力學來描述其運動軌跡，同時由於各粒子間分布距離較遠所以不同粒子的波函數重疊現象不嚴重，而使得氣體分子遵守馬克士威-波茲曼統計 (Maxwell–Boltzmann statistics)[3]。在統計力學中，馬克士威-波茲曼分布函數被表示成：

\(f_{MB}(\epsilon)=Ae^{-\epsilon/K_BT}\cdots(1)\)

，其中 \(f_{MB}(\epsilon)\) 便是指粒子處在能量 \(\epsilon\) 的機率而 \(K_B=1.38\times 10^{-23}\)（單位：焦耳/絕對溫度）是為了紀念波茲曼在統計學上的貢獻而用其名字而命名的波茲曼常數，另外係數 \(A\) 在此扮演機率歸一的角色，也就是說粒子處在所有能量狀態所發生的各種可能的機率總和為一，此外係數 \(A\) 也可與系統的粒子個數有關。

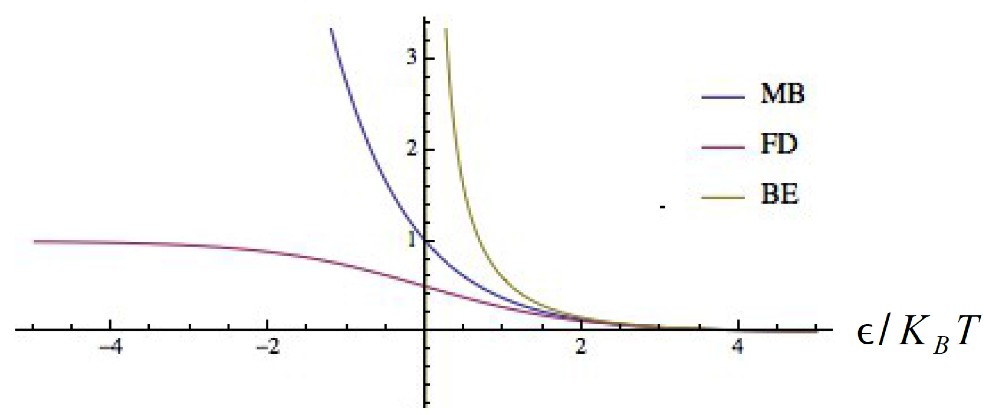
圖一是當系統處在一明確溫度下，粒子處於不同能量的機率分布圖，由圖中我們可以了解到對於馬克士威-波茲曼分布來說，粒子處於較低能量態\((\epsilon \ll K_BT)\)的機率較高，也就是說多粒子系統中的大部分粒子容易處在低能量態，使得系統本身偏好保持最低能量。反過來說，由圖一我們可以了解到粒子處於較高能量態\((\epsilon \gg K_BT)\)的機率較低，也就是說大部分的粒子並不偏好處在高能量態。

此外，我們也可由各粒子運動速率分布的觀點來了解馬克士威-波茲曼分布函數，此時此分布函數可被理解為各粒子運動速率的分佈狀況，其表示式為

\(f(v,K_BT)=\sqrt{\frac{2}{\pi}(\frac{m}{K_BT})^3}v^2e^{\frac{-mv^2}{{2K_BT}}}\cdots(2)\)

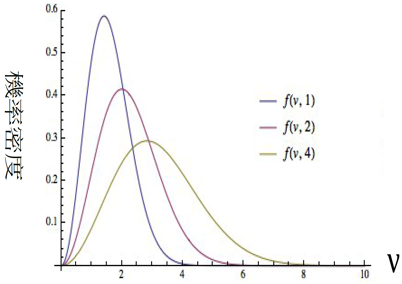
，其中 \(m\) 為粒子的質量。比較公式 \((1)\) 與 \((2)\)，我們可以觀察到用於描述速率分布函數的公式 \((2)\) 的確與公式 \((1)\) 有一樣的數學架構，而能量 \(\epsilon\) 可被理解為粒子的動能 \(\frac{1}{2}mv^2\)。圖二是在不同的溫度下，被馬克士威-波茲曼分布函數所描述的粒子速率分布情況

由圖二我們可以得知當多粒子系統的溫度越高時，粒子最大分布所對應的運動速率則越快。由於動能與粒子運動速度成正比，因此系統所擁有的動能也隨之變大。反之，當系統溫度下降時，系統相對應的動能也就變小，因此，多粒子系統所處在的溫度高低會直接影響其動能與運動速率。

參考文獻

[1] Beiser A.(2003), 近代物理, 普林斯頓國際有限公司.

[2] 維基百科. Maxwell–Boltzmann distribution. http://en.wikipedia.org/wiki/Maxwell–Boltzmann_distribution

[3] Carter A. H.(2001), Classical and statistical thermodynamics, Prentice Hall.