霍爾效應
霍爾效應 (Hall effect)
臺中縣縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理系洪連輝教授責任編輯
霍爾效應(Hall effect) 在 1879 年由 Edwin Hall 發現,其是指將一固體導體(假設固體為一長方體,長邊沿著 \(x\) 軸方向、寬沿著 \(z\) 軸方向且寬度為 \(w\)、高沿 \(y\) 軸方向且寬度為 \(d\),較好分析)通電流,並放置於磁場中,而在導體表面產生電位差的情形,原因很簡單,若導體之電流方向為 \(x\),外加磁場方向為 \(z\),則不論導體中的非束縛電荷帶正電或負電,根據勞倫茲力 \(F=q(E+v\times B)\),都會往 \(-y\) 的方向漂移而產生電位差,此電位差稱為霍爾電壓(Hall voltage),而霍爾電壓,可根據勞倫茲力,計算其電、磁力平衡得到,其推導如下:
已知導體內部只有一種可移動的非束縛電荷且密度為 \(n\),而每個粒子之帶電量為 \(Q\) 且運動速度為 \(v\),而導體帶電流 \(I\),霍爾電壓為 \(V_H\),霍爾電場 \(E\),外部磁場為 \(B\),體電流密度為 \(J\),則根據靜力平衡有(方向都在 \(y\) 軸故不特別討論):
\(QE=QvB\rightarrow\displaystyle\frac{V_H}{d}=\frac{J}{nQ}B\) (明顯有:\(J=nQv \therefore v=\displaystyle\frac{J}{nQ}\))
\(\displaystyle\therefore J=\frac{I}{wd}\rightarrow\frac{V_H}{d}=\frac{1}{nQ}\frac{I}{wd}B\)
\(\displaystyle\therefore V_H=\frac{I}{nQw}B\)
根據以上推導,可知霍爾電壓可測量非束縛電荷的密度(因為上式中僅有 \(n\) 未知,其餘的數值都可經過實驗量測得到)與運動速度(或稱飄移速度),另外,根據測 得霍爾電壓的正負,也可輕易了解其導體內部之非束縛電荷為電子(帶負電)或電洞(帶正電),因為若用三用電表將導體上部(指的是(\(x\)、\(d\)、\(z\))之平面)接正極,下部((\(x\)、\(0\)、\(z\))之平面)接負極測量霍爾電壓,若電壓值為正,則代表負電荷累積於導體之下部,故此時導體內部之非束縛電荷種類為電子,反之,若 測得的霍爾電壓為負值,則載子為電洞。另一項在霍爾效應中非常著名的結果是霍爾係數,從以上推導中,可知:
\(\displaystyle\frac{1}{nQ}=\frac{1}{JB}\frac{V_H}{d}=\frac{E}{JB}\)
其中 \((nQ)^{-1}\) 就是霍爾係數,只和導體的性質有關,和其他實驗變因無關,順帶一提,因為霍爾係數和 \(n\) 成反比,而我們知道金屬中的自由電子(非束縛電荷)非常多,因此金屬的霍爾係數往往非常小,相較之下,半導體的霍爾係數則較大。
霍爾效應在半導體中的應用非常常見,因為其結果簡單的表示了半導體中性質一些性質(例如鑑定此半導體為p型或n型),另外還有霍爾探針(Hall probe) ,其可測量外部磁場之大小,原理很簡單,若已知導體之非束縛電荷密度和其帶電量,則可以另用這項性質反推外部磁場。
近來有發展出所謂的量子霍爾效應,又分為整數量子霍爾效應、分數量子霍爾效應,因為會測量到與材料等皆無關的常數,故分別在 1985 年與 1998 年獲得諾貝爾獎。


 前一篇文章
前一篇文章 下一篇文章
下一篇文章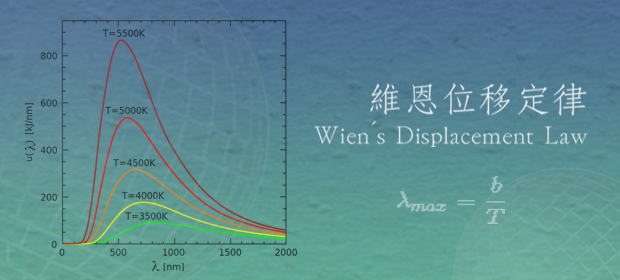 維恩位移定律
維恩位移定律 
