連續方程式

連續方程式 (Continuity Equation)
國立臺灣大學大氣科學系 陳品全

在形容管中一個不可壓縮的流體之運動時，我們常常會使用到一個公式：

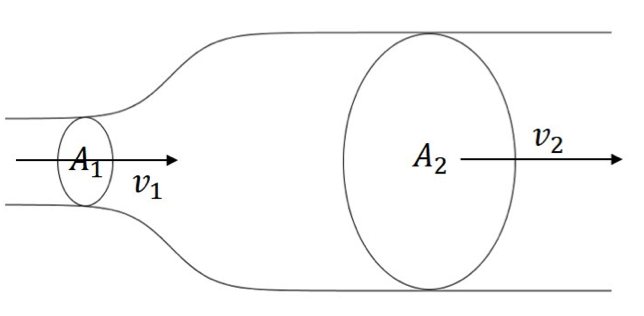
$$A_1v_1=A_2v_2$$

圖一、連續方程式示意圖（本文作者陳品全繪製）

此公式為連續方程式的一個特例，代表流體的質量守恆律。要看出這一點，我們在這個流管取一個假想的控制體積 (Control Volume)，其中 $$A_1$$ 和 $$A_2$$ 分別是左邊和右邊流管截面積，而 $$v_1$$ 和 $$v_2$$ 則是流體的流進和流出速率。在單位時間內，流進的體積 $$A_1v_1\Delta t$$ 會等於流出的體積 $$A_2v_2\Delta t$$，如此一來此控制體積內的流體量才會維持為定值 （穩定流，Steady flow）。

對於更一般的情況，我們也可以有更一般性 (general) 的連續方程式來形容流體。我們可以想像在一個三維的流體中取一個小體積 $$\delta V$$ 作為控制體積，而這個體積內含有的流體質量則是 $$\delta M=\rho\delta V$$。因為控制體積內的質量 $$\delta M$$ 要守恆，所以 $$\frac{d(\delta M)}{dt}=0$$。利用這個等式，我們可以導出：

$$\begin{array}{ll}\displaystyle\frac{1}{\delta M}\frac{d(\delta M)}{dt}&\displaystyle=\frac{\left[\frac{\rho d(\delta V)}{dt}+\frac{d\rho}{dt}\delta V\right]}{\rho\delta V}\\&\displaystyle=\frac{1}{\delta V}\frac{d(\delta V)}{dt}+\frac{1}{\rho}\frac{d\rho}{dt}=0\end{array}$$

對於 $$\displaystyle\frac{1}{\delta V}\frac{d(\delta V)}{dt}$$，我們可以將控制體積假想是一個很小的長方體，邊長分別為 $$\delta x,\delta y,\delta z$$（也就是分別為 $$x$$、$$y$$、$$z$$ 方向的微小變化）。

圖二、極小的長方體 (本文作者陳品全繪製)

$$\begin{array}{ll}\displaystyle\frac{1}{\delta V}\frac{d(\delta V)}{dt}&\displaystyle=\frac{1}{\delta x\delta y\delta z}\frac{d(\delta x\delta y\delta z)}{dt}\\&\displaystyle=\frac{\delta u\delta y\delta z+\delta x\delta v\delta z+\delta x\delta y\delta w}{\delta x\delta y\delta z}\\&\displaystyle=\frac{\delta u}{\delta x}+\frac{\delta v}{\delta y}+\frac{\delta w}{\delta z}\xrightarrow{\delta x,\delta y,\delta z\to 0}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\nabla\cdot\vec{v}\end{array}$$

$$u,v,w$$ 分別是 $$x,y,z$$ 方向的速度，而我們這一項正好是速度的散度 (divergence)。於是我們得到了一個可以形容三維流體的連續方程式：

$$\displaystyle\frac{1}{\rho}\frac{d\rho}{dt}+\nabla\cdot\vec{v}=0$$

這一條連續方程式因為包含了 $$\frac{1}{\rho}\frac{d\rho}{dt}$$，因此是可以用來形容非穩定的流體 (Non-steady flow)。如果流體速度的散度大於零的話，則代表這個控制體積內的流體流出率大於流入率，所以這個控制體積內的密度會隨著時間下降。

這個公式還可以有一個變形：

$$\displaystyle\frac{1}{\rho}\frac{d\rho}{dt}+\nabla\cdot\vec{v}=\frac{1}{\rho}\left(\frac{\partial \rho}{\partial t}+v\cdot\nabla\rho\right)+\nabla\cdot\vec{v}=0$$

$$\displaystyle\rightarrow \frac{\partial \rho}{\partial t}+v\cdot\nabla\rho+\rho\nabla\cdot\vec{v}=\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho\vec{v})=0$$

對於不可壓縮的流體，$$\frac{\partial \rho}{\partial t}=0$$，因此 $$\nabla\cdot(\rho\vec{v})=0$$。在電磁學中，我們常常會把 $$\rho\vec{v}$$ 寫成 $$\vec{J}$$，也就是所謂的電流密度。

補充：Divergence theorem

對於 $$\nabla\cdot(\rho\vec{v})$$，我們可以利用 divergence theorem 寫成

$$\displaystyle\nabla\cdot(\rho\vec{v})=\lim_{V\to 0}\int\nabla\cdot(\rho\vec{v})\frac{dV}{V}=\lim_{A\to 0}\oint(\rho\vec{v})\cdot d\vec{A}$$

故可以想像成是在一個體積非常小的控制體積中，看看流體密度流對於控制面積（Control surface，控制體積的表面）的總通量為何（通常會選擇向外為正）。

更詳細的介紹請見《散度和旋度 (Divergence and Curl)》。

參考文獻

1. 楊明仁。Chapter 3, Kinematics of fluid flow. 流體力學上課講義。
2. Continuity and Conservation of Matter — CIVE1400: Fluid Mechanics, University of Leeds. http://www.efm.leeds.ac.uk/CIVE/CIVE1400/Section3/continuity.htm