絕對零度

絕對零度 (Absolute zero)
國立臺灣大學化學系學士生張育唐/國立臺灣大學化學系陳藹然博士責任編輯

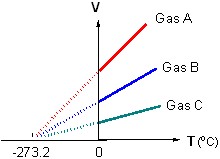
十八世紀前後的科學家對於氣體做了很多研究，發表了許多定律，例如氣體之壓力-體積關係的波以耳定律(Boyle’s law)、體積-溫度關係的查爾斯定律(Charles’s law)等。其中查爾斯定律顯示：無論氣體種類，定壓下氣體的體積和溫度成正比，且這些關係直線最後都與x軸（溫度）交於同一點，即 -273.2°C或是 -459.7°F的地方，表示所有氣體在-273.2°C時體積為0。

圖一、查爾斯定律顯示：無論氣體種類，定壓下氣體的體積和溫度成正比，且體積-溫度直線交於同一點，-273.2°C。 （圖片來源：陳藹然博士）

凱文(William Thomson, 1st Baron Kelvin, 1824-1907)據此定義新的溫標，將 -273.2°C定義為凱式溫標(Kelvin scale)或稱熱力學溫標(Thermodynamic temperature scale)的0度，即0 K。由於氣體的體積是不可能小於零的，所以氣體不可能出現低於0 K，故0 K又稱為絕對零度(Absolute Zero)。絕對零度是熱力學理論中，溫度可達到的最低值，此時系統的熵(entropy)達到其極小值。

根據理想氣體方程式(Ideal gas equation)：

PV = nRT  （P壓力、V體積、n氣體分子數、Ｒ理想氣體常數、Ｔ溫度）

當T = 0時，即可得到PV = 0。分子平均動能E_k = 3kT / 2，其中k為波茲曼常數(Boltzmann Constant)；因此當T = 0時，亦可得知動能為0。氣體粒子有質量，無體積，所以在 T=0, 動能為零下，所有的粒子掉到容器下方，容器中粒子分佈所佔的體積為零。

不過根據量子力學中的海森堡測不準原理(Heisenberg Uncertainty Principle)，一個粒子的位置與動量不可能被同時精確確定：

（Δx = 粒子位置的不確定性，Δp = 粒子動能的不確定性，h = 普郎克常數）

實際上在絕對零度下，仍舊維持著粒子基態的能量， 稱之為零點能量(Zero Point Energy)。零點能量的大小為E₀ = hv / 2，其中h為普朗克常數(Planck Constant)6.626 × 10^-34 J•s，v為頻率。

在低於絕對零度的狀況下，由於分子佔有的體積不可能為負值，得知不可能出現溫度低於絕對零度的情況。然而熱力學第三定律(Third Law of Thermodynamics)指出，當溫度在趨近絕對零度時，該系統的熵變化率ΔS趨近於零；亦即任何系統都不可能透過有限次數、不可逆(irreversible)的步驟來使得系統達到絕對零度。亦即絕對零度亦不可能達到。因此，科學家雖然無法達到絕對零度，但仍舊嘗試著趨近於絕對零度，發現一些低溫物理的相關性質。透過德布羅伊關係式(de Broglie Equation)可以看到：

當溫度逐漸降低時，物質波的波長逐漸上升；因此分子在極低溫的狀態下，會令其量子力學的特性較為明顯。一般而言，若是要達成絕對零度，無法使用正常使用冷卻劑的方式達成，必須透過特殊的方法。常用的方法例如雷射冷卻(Laser Cooling)、蒸發冷卻(Evaporate Cooling)等。目前為止科學家所能得到的最低溫度是冷卻 2×10⁷ 顆 Cs 原子到 1.1×10^-6 K。

資料來源
1. Zumdahl, S. S. Chemical Principles, 5th edition; Houghton Mifflin Company: Boston, 2003; pp. 144-145.
2. Wikipedia–Absolute zero  http://en.wikipedia.org/wiki/Absolute_zero