潤德勒弔詭

潤德勒弔詭 (Rindler Paradox)
國立臺灣大學醫學系100級 林欣妤

為了澄清狹義相對論中關於長度測量以及同時性之概念，潤德勒(Wolfgang Rindler)在1961年提出此一弔詭，又稱「棒子與洞的弔詭」(rod and hole paradox)。狹義相對論告訴我們，觀測一個以接近光速移動的物體時，會發現它的長度變短了 (為原本的  \(\sqrt{1-\frac{v^2}{c^2}}\) 倍) ！

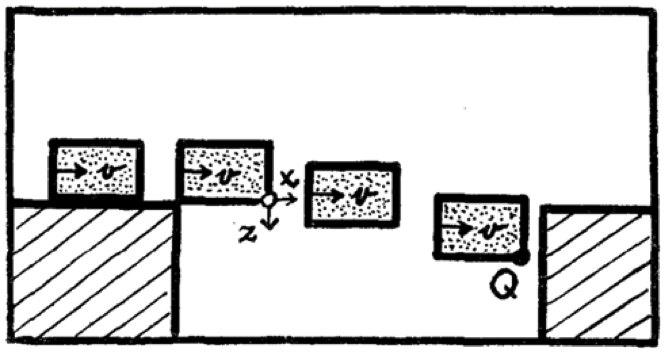
假設有個棒狀的剛體在桌上高速前進，遇到一個和它靜止時長度相同的洞，那棒子是否會掉進洞裡呢？現在有兩位觀察者，\(A\) 相對靜止於桌面，而 \(B\) 跟著棒子高速移動。對 \(A\) 來說棒子高速接近桌上的洞，由相對論我們知道，他會認為棒子的長度變短，在飛過洞的一小段時間中棒子下落了一點，最終掉進洞裡(Fig. 1)。

Fig.1 由 \(A\) 的觀點，長度縮短的棒子受重力影響下墜到洞中

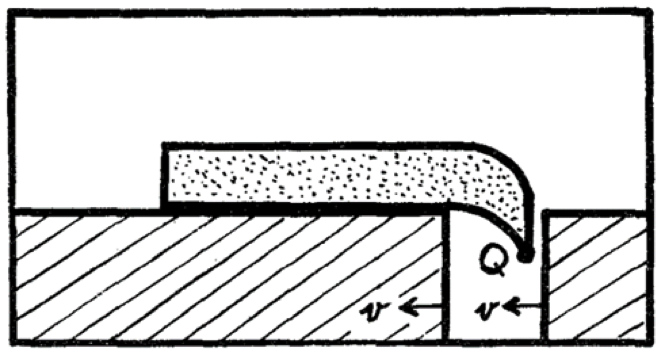
可是由 \(B\) 的觀點，是洞高速接近棒子(棒子本身則是靜止)，洞的長度變短，使得棒子能經過它不會掉進去！棒子開始經過洞上方時，會受到地心引力影響而有向下的加速度；但仍在桌面上的一部分，並不會感受到重力加速度。此處衍生出一個有趣的問題，當棒子前端開始“下墜”而後端仍在桌面上，在 \(B\) 的世界裡，棒子看起來是彎曲的，如潤德勒所畫的圖(Fig. 2)：

Fig.2 不均勻受力使原本為剛體的棒子在 \(B\) 的觀測中呈現彎曲

如最初所述，棒子是「剛體」，可是在 \(B\) 的眼中它卻彎曲了。然而材質的固有性質似乎不應該因觀察者的速度差異而有所改變？亦或人們需要重新思考「剛體」的定義，來合理解釋近光速時納入相對論效應的事件呢？

回到弔詭本身，對於 \(B\) 觀察者，因為棒子不同位置具有不同加速度，這個情況不方便用狹義相對論處理，所以我們在洞頂端加一個門，當 \(A\) 看到棒子的尾端經過洞的邊緣時就把門朝下快速打開，如此一來整根棒子都均勻受到重力加速度，避開剛才的情形。

當棒子底部低於洞口高度時，我們認為棒子最終會受到遠端牆壁的阻擋而掉進洞中。潤德勒假設門一打開，整根棒子在垂直方向會同時受重力作用，那麼不論是 \(A\) 或 \(B\) 都能發現在這一小段「懸空」的時間裡棒子會下墜（或朝下扭曲）一點點，因此棒子會掉進洞裡！

2005年瑞士的科學家則把上述理想化的模型做修改，期望使這個例子更貼近實際會碰到的狀況，即他們假設棒子懸空的部分在垂直方向除了受重力加速度外，還要考慮棒子的彈性所造成應力的傳播速度之影響。由於這個分析並不像潤德勒原始模型般能直接用來澄清相對論基本概念，此處不再多述。

另一個跟長度收縮有關的例子是「梯子弔詭 (ladder paradox)」（或稱穀倉-竿弔詭 barn-pole paradox）：一把梯子以近光速進入一座倉庫並從另一端離開，梯子的靜止長度比倉庫深度大。對倉庫而言，長度收縮使某個時間點梯子恰好能完全容納在倉庫裡，但對梯子來說，倉庫一直都過淺而無法裝的下它。這個弔詭可以用相對論中的同時性(simultaneity) 概念來解釋，而且免去了潤德勒弔詭中力傳遞的困擾。

參考文獻

1. Wolfgang R. (1961) Length Contraction Paradox. American Journal of Physics, 29, 365-366.
2. Harald van L. and Christian G. (2005) The Rod and Hole paradox re-examined. European Journal of Physics, 26, 19–23.