夫朗和斐繞射

夫朗和斐繞射(Fraunhofer Diffraction)
國立臺灣大學物理學系 周文鴻

夫朗和斐繞射 (Fraunhofer diffraction) 與菲涅耳繞射 (Fresnel diffraction) 分別是兩種描述繞射現象的模型；夫朗和斐繞射假設造成繞射的狹縫和屏幕距離很遠，可視為無限遠的情況，而菲涅耳繞射則假設屏幕與狹縫的距離是有限的。圖一說明了這種幾何關係的差異。圖一 (b) 中點光源與狹縫間置放透鏡，目的只是讓入射光線變成平行光；而實務上，如果要符合夫朗和斐繞射的條件，只要在狹縫至屏幕間放一個凸透鏡聚光，就能將屏幕視為在無限遠處)。因為屏幕與狹縫距離視為無限遠，所以可以將夾角 $$\theta$$ 近似：

$$\displaystyle\tan\theta=\frac{y}{d}\approx\sin\theta\approx\theta~~~~~~~~~(1)$$

圖一、(a) 符合菲涅耳繞射的情況。(b) 符合夫朗和斐繞射的情況。(c) 屏幕上 P 點離中心點的距離為 y，屏幕與狹縫距離為 d，當 d 視為無限大時 (1) 式就能成立。（本文作者周文鴻繪） 

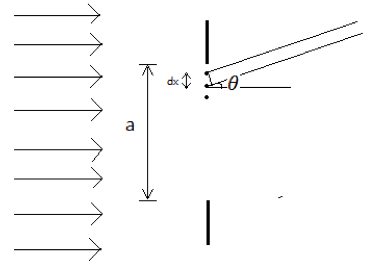
在符合夫朗和斐繞射假射的條件下，我們可以解釋單狹縫繞射形成的亮暗相間的條紋（圖二）。首先，根據惠更斯原理 (Huygen’s principle)，波前的每一點都可視為點波源放出球面波。光源發出的光經過狹縫時，只有狹縫開口處的光才能通過，而我們將狹縫每一處都視為新的點波源發出光到屏幕上。從以上描述，我們可以定性找出繞射條紋暗紋的位置，而定量分析則能幫我們求出亮紋的位置。

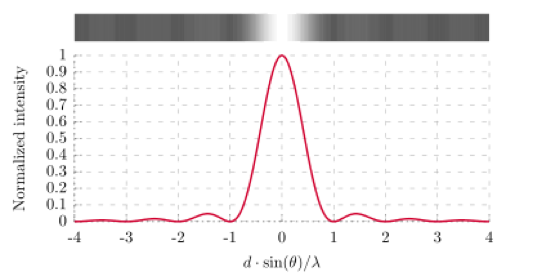
圖二、單狹縫繞射強度分布圖。（圖片取自：http://commons.wikimedia.org/wiki/File:Single_Slit_Diffraction_(english).svg#/media/File:Single_Slit_Diffraction_(english).svg）

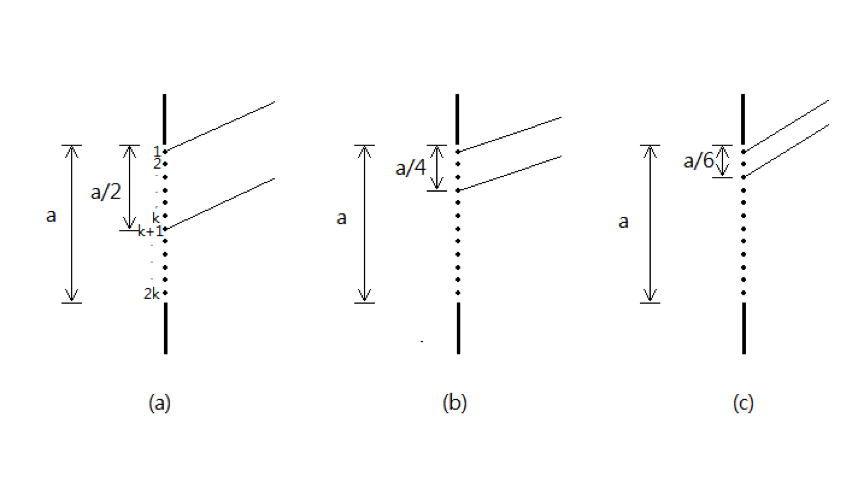
定性來說，讓我們先將狹縫分為 2k 等分，每一等分都構成一點光源。以圖三 (a) 來說明，如果 1 號點光源及 k + 1 號點光源發出的光線到達屏幕某一點時，因光線走的距離（光程差）不同，造成相位完全相反，那這兩束光就會形成完全破壞性干涉。而鄰近的 2 號點光源及 k+2 號點光源光程差也應該完全一樣，因此也產生完全破壞性干涉，3 號點光源及 k + 3 號點光源也產生完全破壞性干涉……以此類推，所有點光源都能與其對應的點光源產生完全破壞性干涉，因此屏幕上該點就會是暗的。

從圖中可以看到，因為狹縫與屏幕距離視為無限遠，兩道光就可視為平行光，因此 1 號點光源和 k+1 號點光源的光程差就是兩條平行線的垂直距離 $$\frac{a}{2}\sin\theta$$。而完全破壞性干涉的條件是「光程差為半波長」，以方程式表達就是 $$\frac{a}{2}\sin\theta=\frac{\lambda}{2}$$，把式 (1) 帶入 $$\sin\theta$$ 即可得到第一暗紋的位置：$$y=\frac{2D\lambda}{a}$$。我們也可以把狹縫繼續細分為 4k 等分、6k 等分……（圖三 (b) 與 (c)），也都可以使點光源兩兩互相產生完全破壞性干涉，所以所有暗紋都符合 $$\frac{a}{2m}\sin\theta=\frac{1}{2}\lambda$$：

$$\displaystyle a\sin\theta=m\lambda,~~~m=1,2,3…~~~~~~~~~(2)$$

圖三、定性描述繞射暗紋產生原因。(a) 狹縫分為兩等分 (b) 四等分 (c) 六等分，每個點光源皆能找到相對應的點光源，產生完全破壞性干涉，互相抵消。（本文作者周文鴻繪）

定量來說，光的強度與其電場大小有關，因此我們必須設法求出狹縫中每一點光源傳播到屏幕上的電場量值，而根據波的疊加原理 (Superposition principle)，將個別電場量值加總就能得到總電場量值，進而能求出屏幕上光的強度。我們先假設點波源之間的寬度為 $$dx$$，因此狹縫寬可表示為 $$a=(2k-1)dx$$。相鄰點光源間的光程差為 $$dx\cdot \sin\theta$$，而相位差為：

$$\displaystyle\varphi=\frac{2\pi}{\lambda}\sin\theta~dx~~~~~~~~~(3)$$

假設 1 號點光源在屏幕上 P 點的電場強度 $$E=\cos\omega t$$，那麼 2 號點光源在屏幕上的電場強度就會差一個相位 $$E=\cos(\omega t-\varphi)$$，依此類推，所有點光源造成的電場即為個別之加總：

$$E=\cos\omega t+\cos(\omega t-\varphi)+\cdots+\cos[\omega t-(2k-1)\varphi]~~~~~~~~~(4)$$

利用數學上的和差化積技巧，可以將上式改寫為

$$\displaystyle E=\frac{\sin(\frac{2k\varphi}{2})}{\sin(\frac{\varphi}{2})}\cos[\omega t-\frac{1}{2}(n-1)\varphi]~~~~~~~~~(5)$$

因為我們將狹縫分為無限個點光源，所以取極限 $$n\to\infty$$，$$dx\to 0$$，$$2k\cdot dx\to a$$。帶入式 (3) 後可得到 $$\frac{2k\varphi}{2}=\frac{\pi}{\lambda}(2k)\sin\theta dx=\frac{\pi a\sin\theta}{\lambda}$$，而 $$\frac{\varphi}{2}=\frac{\pi a\sin\theta}{n\lambda}\to 0$$。令 $$\beta=\frac{\pi a\sin\theta}{\lambda}$$，則電場 $$E$$ 可近似為：$$E=A\frac{\sin\beta}{\beta}\cos(\omega t-\beta)$$。其中，後方的 $$\cos$$ 項代表電磁波的傳遞，而前方係數則代表電場振幅，而光強度正比於電場振幅平方：

$$\displaystyle I=I_0\frac{\sin^2\beta}{\beta^2}~~~~~~~~~(6)$$

當 $$\sin^2\beta=0$$ 時，光強度為 0，也就形成暗紋，條件是 $$\beta=m\pi$$，$$m$$ 是非零整數。將 $$\beta$$ 的定義帶入，我們就能再度得到式 (2)。亮紋的位置則比較難求得，首先當 $$\beta=0$$ 時，$$\frac{\sin^2\beta}{\beta^2}$$ 為不定型，但藉由微積分中的 L’Hospital 法則我們發現它其實趨近於 1，此時 $$I=I_0$$ 為中央亮紋的強度。其他亮紋位置在亮度最大值的地方，因此我們將強度 $$I$$ 對 $$\beta$$ 微分：

$$\displaystyle \frac{dI}{d\beta}=I_0\frac{2\sin\beta\cos\beta\cdot\beta^2-2\beta\cdot\sin^2\beta}{\beta^4}=0~~~~~~~~~(7)$$

化簡後，發現極值產生在 $$\sin\beta(\beta-\tan\beta)=0$$ 處，而 $$\sin\beta=0$$ 代表極小值，也就是暗紋位置，所以亮紋位置在 $$\tan\beta=\beta$$ 處。因為上式的解不能以基本函數表達，因此只能用數值解，或是將方程式的解視為 $$y=\tan\beta$$ 及 $$y=\beta$$ 兩條直線交點求近似解（圖五）。

圖四、將狹縫細分為間隔為 dx 的點光源，光線與平行線夾角為 θ，故兩條光線間距離為 dx．sinθ。（本文作者周文鴻繪）

圖五、圖中藍線為 y = tanβ，綠線為 y = β，兩條直線交點的 β 值就是對應亮紋產生的位置。（本文作者周文鴻繪）

參考文獻

1. Ghatak, A. (2010). Optics. Boston: McGraw-Hill Higher Education.
2. Fraunhofer diffraction – Wikipedia. http://en.wikipedia.org/wiki/Fraunhofer_diffraction
3. Fraunhofer Diffraction Geometry – Hyperphysics. http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/fraungeo.html#c1